В современной виртуальной образовательной среде большую роль могут играть компоненты, обладающие свойствами адаптивности и интерактивности. К таким компонентам относятся различные обучающие и тестирующие программы, виртуальные тренажеры. По этой причине актуальным является вопрос разработки новых адаптационных стратегий самоорганизации таких компонентов. К числу наиболее существенных вопросов, требующих решения, относится вопрос создания алгоритма, реализующего адаптацию программы на основе многоконтурных обратных связей. Помимо регуляции состояния программного компонента в зависимости от действий пользователя, в ряде случаев может быть необходим учет состояния среды выполнения и доступных аппаратных ресурсов. В данной работе приведено описание алгоритма, учитывающего все обозначенные факторы.
Структура, математическая модель и способ создания адаптивного программного компонента виртуальной образовательной среды
Создание алгоритма, эффективно реализующего адаптацию по нескольким контурам обратной связи, требует особого способа организации адаптивной программы. Первоочередная задача – разработка математической модели программы, которая позволит описать основные компоненты программы, взаимосвязи между ними, а также процессы, протекающие в программной системе, в структурированной форме, удобной для последующей алгоритмизации.
С целью создания такой модели было решено применить методы морфологического анализа и синтеза [1]. Результатом выполнения этапа морфологического анализа является морфологическое множество, называемое также множеством альтернатив, содержащим в себе описание всех возможных вариантов системы. В процессе морфологического синтеза осуществляется поиск на морфологическом множестве оптимальной структуры синтезируемого объекта.
Для задания морфологического множества, описывающего структуру адаптивной программы, используются диаграммы характеристик – расширенные И/ИЛИ-деревья [2, 3]. Пример структуры адаптивной программы в формате диаграммы характеристик представлен на рисунке.
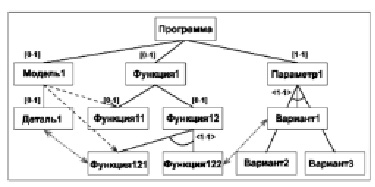
Структура адаптивной программы в формате диаграммы характеристик
Для обеспечения удобства последующей алгоритмизации и обработки было принято решение использовать гиперграфовое представление описания структуры, заданного в форме диаграммы характеристик. При данном преобразовании к основным элементам диаграммы характеристик будут применяться следующие правила [4]:
1. Множество характеристик модели будет отображено на множество вершин соответствующего гиперграфа Features > V.
2. Множество взаимоотношений модели будет отображено на множество гиперребер, соединяющих вершины гиперграфа (характеристики модели) Relations > E.
В данной работе предлагается следующая математическая модель:
,
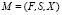где F – представление структуры адаптивной программы в форме ориентированного гиперграфа, полученного на основе диаграммы характеристик;
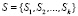– конечное множество конфигураций диаграммы характеристик, каждая из которых является описанием определенного состояния адаптивной программы (подграфом исходного гиперграфа);
X – матрица переходов между состояниями программы.
Как видно, предложенная математическая модель изменчивости является достаточно наглядным и удобным инструментом синтеза структуры адаптивной программной системы. Элементы данной модели служат для описания пространства возможных состояний программы.
Метод синтеза адаптивного программного компонента, базирующийся на предложенной математической модели, включает в себя следующие этапы:
1. Этап морфологического анализа адаптивного программного компонента. В ходе выполнения этапа разрабатывается структура программы в формате диаграммы характеристик, выполняется определение пространства параметров элементов диаграммы.
2. Этап теоретико-множественного преобразования структуры программного компонента. Результатом выполнения этапа является гиперграфовое представление полученной на предыдущем этапе структуры.
3. Этап генерации состояний адаптивной программной системы. Результатом выполнения этапа является множество конфигураций исходной диаграммы характеристик, описывающей структуру программы. В процессе разработки программной системы пользователем вручную определяются необходимые структурные конфигурации, являющиеся базовыми для синтезируемой структуры программы. В процессе выполнения на основе имеющихся базовых конфигураций формируются производные промежуточные конфигурации. Данный процесс является частью более широкого процесса адаптации в ходе выполнения программной системы.
4. Этап верификации системных пользовательских конфигураций. Основное назначение этапа – поиск и исправление ошибок в системных конфигурациях, описывающих отдельные состояния адаптивной программной системы.
5. Этап определения взаимосвязей между состояниями. Результатом выполнения данного этапа является матрица переходов.
Предложенный метод синтеза адаптивных программных компонентов виртуальной образовательной среды, основанный на гиперграфовом подходе к формализации диаграмм характеристик и построению на их основе системных конфигураций, позволяет формализовать сложную математическую процедуру задания изменчивости наглядным, простым и интуитивно понятным образом с использованием средств визуального проектирования.
Алгоритм автоматического ситуационного выбора системных конфигураций в процессе выполнения
В общем случае об адаптивности в программной системе можно говорить тогда, когда использование текущей информации в ней приводит к изменению алгоритма функционирования. Адаптивную систему, если структура алгоритма в ней не изменяется, а изменяются только параметры, называют самонастраивающейся. Если изменяется структура системы, то ее называют самоорганизующейся. В такой системе процессы самоорганизации присутствуют на всех последующих этапах жизненного цикла [5, 6, 7].
Специфика функционирования адаптивного программного компонента подразумевает наличие трех контуров обратной связи в программной системе:
1) контур, реализующий адаптацию в зависимости от действий пользователя;
2) контур, реализующий адаптацию в зависимости от состояния среды выполнения;
3) контур, реализующий адаптацию в зависимости от доступных аппаратных ресурсов.
Адаптация в соответствии с доступными аппаратными ресурсами является, по сути, параметрической адаптацией. Данный тип адаптации особенно актуален для программного обеспечения, использующего трехмерную графику (например, виртуальных тренажеров) и подразумевает влияние производительности системы на степень детализации геометрических объектов. Степень геометрической детализации, в свою очередь, является параметром соответствующего элемента модели характеристик. Таким образом по данному контуру управления осуществляется процесс самонастройки программы.
Рассмотрим реализацию необходимого алгоритма применительно к программным компонентам, использующим трехмерную графику. Предлагаемый алгоритм ситуационного выбора конфигураций в данном случае включает в себя следующие шаги:
1. Установка номера текущей конфигурации i = 1.
2. Выбор конфигурации Si.
3. Вычисляется показатель P производительности вычислительной системы
,
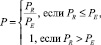где PR – производительность ЭВМ, на которой запускается программа;
PR = k·P0 – производительность эталонной ЭВМ;
k – коэффициент, определяемый автором программы (по умолчанию k = 1);
P0 – производительность ЭВМ, на которой создавался программный компонент.
4. Первый этап параметрического синтеза программного компонента: на основе полученного коэффициента производительности системы происходит выбор соответствующего уровня детализации трехмерных моделей. На диаграмме характеристик узел, соответствующий трехмерному объекту, может содержать несколько геометрических моделей разной степени детализации. Они упорядочены по возрастанию уровня сложности. Если некоторый объект О имеет n уровней детализации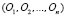 
, то при визуализации данного объекта будет выбран вариант Oi, где 
, 
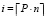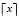– целое число, ближайшее к x, 
.
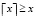5. Развертывание поддеревьев моделей, функций и параметров. Ожидание завершения состояния.
6. Осуществляется вычисление показателя качества работы пользователя. При d > 0 формула расчета будет иметь следующий вид:
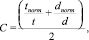
где t – время пребывания системы в текущем состоянии;
d – количество ошибок, случившихся при выполнении шага;
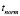и 
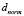– нормальные значения показателей t и d, задаваемые автором приложения для каждой конфигурации. В случае если d = 0, формула заменяется на следующую:
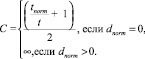
7. Второй этап параметрического синтеза программного компонента: определение значений параметров, используемых в функциях. Параметры могут принадлежать к одному из трех типов – целое число, вещественное число, перечисление. В первых двух случаях автор должен задать пару граничных значений (xнач, хкон), в пределах которых параметр может принимать свои значения. В последнем случае автор должен перечислить значения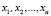 
. Для расчета параметров необходимо провести вычисление нормализованного показателя 
. Для начала нужно отобразить интервал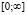 
, которому принадлежит С, на интервал [0; 1], например, с помощью следующего преобразования:
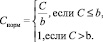
где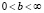 
– наибольшее значение показателя С, определенное для текущего состояния. Другой возможный вариант преобразования выглядит следующим образом:
,
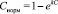где k > 0 – некоторый коэффициент, позволяющий настроить вид преобразования. После того как получено нормированное значение показателя работы пользователя с состоянием, вычисляются значения параметров, используемых в следующем состоянии. В случае если параметр является целым или вещественным числом, для которого заданы граничные значения (xнач, хкон), то значение параметра находится по формуле
.
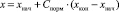Если параметр является перечислением, то его значение равно x = xi, где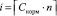 
, 
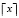– целое число, ближайшее к x, 
.
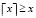8. Если это необходимо, корректировка матрицы переходов с учетом состояния среды выполнения
,
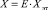где Xэт – исходная матрица переходов, задаваемая пользователем для Е = 1;
E – показатель, определяющий состояние среды выполнения. Данный показатель вычисляется на основании множества значений показателя С, характеризующих то, как пользователь работал с несколькими последними состояниями программы. В случае если среда выполнения оказывается слишком сложной для пользователя (значения показателя С по результатам прохождения нескольких последних состояний являются низкими), то происходит уменьшение значения показателя E и, соответственно, сужение диапазонов значений, расположенных в ячейках матрицы. При усложнении среды выполнения происходит увеличение значения показателя E.
9. Если существует такой интервал xij, что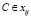 
, то i = j и осуществляется переход к пункту 2 алгоритма. Иначе работа программы завершается.
Заключение
В работе был предложен алгоритм автоматического ситуационного выбора системных конфигураций в процессе выполнения адаптивного программного компонента виртуальной образовательной среды, который, в отличие от известных, использует трехконтурную систему обратных связей. Данные связи регулируют текущее состояние программы в зависимости от действий пользователя, состояния среды выполнения и доступных аппаратных ресурсов.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 15-07-01553.