В настоящее время заключительная стадия процесса первичной обработки хлопка (ПОХ) – линтерование – ведется либо без средств автоматизации, либо с весьма ограниченным применением таковых. Имеющиеся разработки, например, для мониторинга отдельных стадий (ПОХ) требуют более совершенных средств контроля и автоматизации отдельных составляющих сложного разветвленного процесса. Так для мониторинга и автоматизации процессов сушки и джинирования разработана автоматизированная система управления, которая, однако, имеет ограниченное применение вследствие трудности контроля заключительной стадии ПОХ.
Что касается этой стадии – линтерования, то к конечной продукции этого процесса предъявляются различные требования в зависимости от назначения выходного материала. Выходным контролируемым технологическим параметром на этой стадии является, как правило, опушенность. Применяемый в соответствии с ГОСТами метод требует длительного времени и для оперативного управления может быть применим только с большой задержкой. За это время при современной производительности линтерных машин (при первом линтеровании от 3500 до 5000 кг/ч) большой объем конечной продукции будет некондиционным, что ведет как к финансовым потерям, так и перерасходу ресурсов и опосредованно к ухудшению экологических показателей, нарушающих требования ГОСТов семейства ISO 14000.
Для исправления этого недостатка была разработана САУ линтерования, которая позволяет вести линтерование в автоматическом режиме.
Целью статьи является исследование процесса линтерования на качество переходного процесса при различных структурах системы автоматического управления и в сравнении с существующими вариантами управления по визуальному контролю и по данным лабораторного анализа опушенности семян лабораторным методом.
Экспериментальная часть
Согласно [4] обратная связь в САУ линтерованием представляет собой некоторую подсистему, включающую в себя два фотоэлемента и вычислительное устройство, выполняющее функцию сравнения сигналов, поступающих с чувствительных элементов, путем деления одного сигнала на другой.
Сигналы на фотоэлементы в свою очередь подаются один от эталона семян, а второй – от потока семян на выходе линтера. При этом согласно [1] отношение может вычисляться для двух случаев
(1)
где Wк – передаточная функция по каналу «выход линтера > выход контрольного преобразователя»; Wэ – передаточная функция по каналу «выходной сигнал эталона > выход эталонного преобразователя». Учитывая динамические свойства линтера и то, что фактически вычисляется отношение двух оригиналов, то это – оригиналы
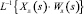и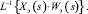 
Так как второй оригинал величина постоянная, не зависящая от контролируемого параметра, то в первом из отношений (1) ε будет описано передаточной функцией Wк.
Для этого в среде MathLab Simulink была построена модель САУ линтерования для обоих способов вычисления отношения ε при управлении, по одному и по двум входам (рис. 1).
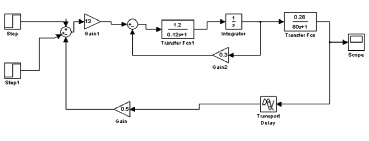
Рис. 1. Схема модели САУ
При задании по одному входу единичная ступенька подается через блок Step. А при подаче задания по двум единичные ступеньки подаются посредством блоков Step и Step1.
В схеме модели системы присутствует звено чистого запаздывания, которое не оказывает влияния на величину отношения сигналов от эталонной пробы и от контролируемого потока, но его присутствие необходимо для транспортировки семян к контрольной камере устройства обратной связи. Это звено оказывает влияние на качество регулирования (управления), увеличивая показатели колебательности переходного процесса, что приводит к выходу некондиционной продукции.
При выбранных параметрах модели САУ получен колебательный переходной процесс, как для задания по одному входу (рис. 2), так и для подачи задания по двум входам (рис. 3).
В обоих случаях система является статической и, следовательно, имеет некоторую ошибку, которую можно определить из передаточной функции по ошибке
Фx(s) = 1 – Ф(s),
где Ф(s) – главный оператор системы или через оператор дифференцирования x(t) = Фx(s)•g(t) и сравнить ее с ошибкой без регулирования, при ручном управлении, по результатам лабораторного анализа, как это делается в настоящее время. Исходя из этих рассуждений, становится возможным оценить целесообразность введения автоматического управления линтерованием, воспользовавшись интегральным критерием качества процесса регулирования 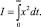[2]
(2)
При задании по одному входу переходный процесс затухает и входит в пятипроцентную трубку допуска примерно через 180 с. Точное значение времени переходного процесса, которое использовалось в дальнейшем, было взято из опции «Workspace» среды MathLab Simulink. Численное значение приведено ниже по тексту.
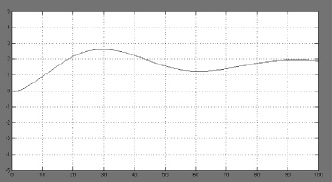
Рис. 2. График переходного процесса при задающем воздействии, подаваемом на вход системы
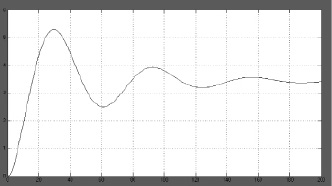
Рис. 3. График переходного процесса при двух задающих воздействиях, подаваемых на вход системы и в цепь обратной связи
При задании и по второму входу, когда в качестве эталонной пробы выбираются семена произвольной заранее известной опушенности (рис. 1) ступеньки в блоках Step и Step1 равны по единице и, соответственно, выходная величина будет иметь значение в два раза большее, чем при управлении по одному входу со ступенчатым воздействием равным 1. Таким образом, и выходная величина на графике (рис. 3) в силу принципа суперпозиции будет иметь удвоенное значение по отношению к значению полученному на графике рис. 2.
Сравнивая полученный результат численного интегрирования кривой на рис. 2 с регулированием при лабораторном анализе даже при минимальной допустимой ошибке в 5 % опушенности и времени, затрачиваемом на проведение анализа, – 2 ч, видно, что автоматическое регулирование почти в 3 раза – 39,073 (рис. 4) против 100 отн. ед. улучшает показатель выхода кондиционного продукта.
На обоих графиках по оси ординат отложено значение съема линта в относительных единицах, что соответствует изменению опушенности Для графика на рис. 1 съем линта, равный соответствует 1,56 отн. ед. На втором графике соответственно – 3,12 отн. ед.
Численное интегрирование проведенное для случая с двумя входами (суммарное входное воздействие равно двум единицам), выполненное в среде MathCad, показано на рис. 5. Интеграл (2) на отрезке времени от начала регулирования до времени 200 с окончания переходного процесса численно равен 146,84 отн. ед.
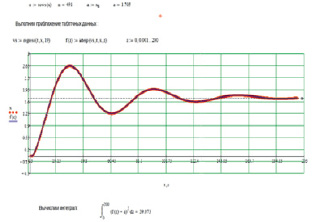
Рис. 4. Скриншот численного интегрирования кривой переходного процесса для случая регулирования по одному входу
Значение времени окончания переходного процесса так же, как и в первом случае, определено из опции «Workspace» среды MathLab Simulink. Сравнивая полученный результат с регулированием при лабораторном анализе при ошибке в 5 % опушенности и времени, затрачиваемом на проведение анализа, – 2 ч, видно, что автоматическое регулирование более чем в 2 раза (146,8 против 360 отн. ед.) улучшает показатель выхода кондиционного продукта. В абсолютных цифрах при производительности одного линтера до 3500 кг/ч по семенам уменьшения выхода некондиционных продуктов снизится до значения не более 1600 кг при условии, что без регулирования вся партия семян становится некондиционной и требуется либо повторное линтерование, либо использование продуктов линтерования по – другому назначению.
На обоих графиках (рис. 4 и 5) синим цветом показана кривая переходного процесса полученная симулированием в среде MathLab Simulink.
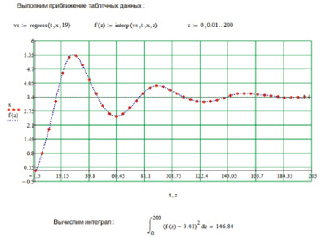
Рис. 5. Скриншот численного интегрирования кривой переходного процесса для случая регулирования по двум входам
Красным цветом показана аппроксимирующая кривая, полученная в среде MathCad. Аппроксимация проводилась методом наименьших квадратов.
При перемене мест делимого и делителя в устройстве обратной связи отношение сигнала от эталона и выходной величины линтера будет выглядеть как
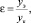(3)
поскольку yэ(t) = kэОэ, где yэ – выходной сигнал преобразователя камеры с эталонным образцом; kэ – коэффициент преобразования фотоэлемента в этой камере; Оэ – опушенность эталонного образца семян, а yк(t) = L–1{X(s)·Wл(s)}, где yк – выходной сигнал линтера, то есть опушенность семян на выходе из линтера; X(s) – изображение Лапласа входного сигнала линтера; Wл(s) – передаточная функция линтера, и выражение (3) запишется как
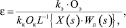(4)
где kк – коэффициент преобразования фотоэлемента в контрольной камере, причем kэ = kк и Ок – установившееся значение опушенности семян на выходе линтера, равное требуемому Оэ.
Тогда, если на вход линтера приложен единичный импульс δ(t), изображение которого X(s) = 1, отношение (4) будет равно
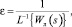
или, учитывая, что линтер как объект управления описывается передаточной функцией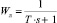 
, а оригинал этого изображения
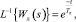
то отношение будет равно
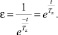(5)
В этом случае оригиналу (5) соответствует изображение
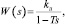
где kл – передаточный коэффициент линтера по каналу управления; Т – постоянная времени линтера.
Таким образом, в системе имеется не минимально фазовое звено. В этом случае, прежде всего, требуется определить: может ли быть такая система в принципе устойчивой [3]. Если существует область устойчивости, то необходимо провести анализ условий устойчивости, т.е. определить границы возможных изменений параметров структурных блоков системы и возможности их конкретной реализации. Это отдельная задача и в этой статье она не рассматривается.
Выводы
Проведенный анализ и сравнение качества регулирования процесса на стадии линтерования показали, что использование автоматической системы позволяет уменьшить количество некондиционной продукции в 2–3 раза в зависимости от выбранного варианта задания в САУ и при производительности современных линтеров максимально может составить от примерно 1600 до 1200 кг/ч на один линтер. Качественные показатели управления улучшаются вследствие замены длительного метода определения опушенности временем транспортного запаздывания необходимого для подачи линтерованных семян под окно контрольной камеры устройства обратной связи [5].
При этом в целях повышения оперативности производства продукции требуемого качества возможно использовать эталонный образец любой опушенности, но с заранее известным коэффициентом отношения величин фото ЭДС генерируемой при отражении от семян с требуемой опушнностью и от семян используемых в качестве эталона.