Увеличить достоверность распознавания наночастиц серебра на поверхности текстильных волокон позволяют корреляционные поляризационные характеристики рамановских спектров исследуемых образцов материалов. В связи с этим значительный интерес представляет проведение статистического моделирования корреляционных параметров интенсивности рамановских спектров волокон с наночастицами серебра при решении системы уравнений векторно-матричного аналитического вида корреляционных эллипсов взаимозависимых параметров с определением координат пересечения [1–6].
В данной работе рассматривается метод векторно-матричного решения системы нелинейных уравнений, составленных на основе корреляционных данных об обьекте системы наночастицы – полиэфирное волокно. Оценить точность решения системы векторно-матричных уравнений предлагается при сравнении по 3 видам решения задачи: с аналитической формой решения системы уравнений, с экспериментальными данными при генерации корреляционных зависимостей и ручным методом отыскания пересечения эллипсов распределения в аналитической форме.
Цель работы – повышение точности распознавания наночастиц серебра на поверхности текстильных материлов по поляризационным характеристикам рамановских спектров с использованием методов векторно-матричной аналитической оценки пересечения эллипсов распределения интенсивности поляризационных рамановских спектров.
Материалы и методы исследования
При проведении эксперимента полиэфирные волокна (ПЭ) были обработаны коллоидным раствором, содержащим наночастицы серебра. На следующем этапе с использованием сканирующего зондового микроскопа (СЗМ) с конфокальным рамановским и флуоресцентным спектрометром OmegaScope™ – в региональном центре нанотехнологий при ЮЗГУ были получены рамановские спектры волокон, покрытых и не покрытых наночастицами серебра. Всего для исследования было выделено пять информативных пиков.
В ходе предварительных экспериментов по измерению случайных значений распределения интенсивностей пиков спектров рамановского комбинационного излучения при этом выявлены корреляционные матрицы и параметры распределений (математические ожидания и средние квадратические отклонения) с учетом поляризации излучения поперек и вдоль волокон одновременно за одно измерение [9].
На следующем этапе было проведено моделирование статистических данных для выявления пересечений эллипсов распределений значений интенсивностей пиков спектрограмм [8, 10]. Генерация заданного количества случайных значений проводилась по нормальному закону с использованием встроенных функций математического редактора MathCad Edition 14, а также методике, предложенной авторами статьи и изложенной в работе [7].
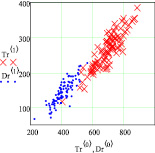
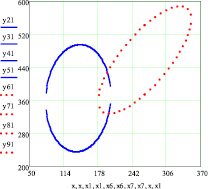
Сгенерированные 96 значений данных для 2 пика рамановского спектра полиэфирного волокна с нанчастицами серебра по оси Х и Y приведены на рис. 1, а, а для 8 пика – на рис. 1, б.
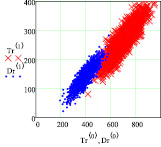
Так как данные рис. 1, а пересекаются, то можно легко найти точку пересечения. По данным рис. 1, б видно, что эллипсы распределения не пересекаются. Поэтому необходимо сгенерировать большее количество данных. На рис. 1, в и г приведены 1600 сгенерированных данных. По ним видно, что по 2 пику эллипсы пересекаются со значительным перехлестыванием, а эллипсы распределения 8 пика пересекаются нормально.
На рис. 2 приведены пересечения аналитических эллипсов распределения данных пиков спектрограмм. Эти эллипсы построены по аналитическим математическим выражениям с параметрами математических ожиданий, средних квадратических отклонений и коэффициентов корреляции для волокон полиэфира без наночастиц (сплошная кривая) и с наночастицами (кривая точками). Для удобства построения эти рисунки развернуты на 180° вокруг оси Х по сравнению с рис. 1.
 а
а 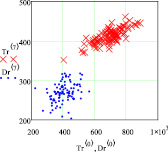 б
б
 в
в 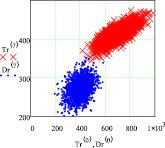 г
г
Рис. 1. Двухмерные корреляционные зависимости рамановских поляризационных спектрограмм полиэфирных волокон с наночастицами серебра: а, б – общий вид при генерации n = 96 данных для 2 и 8 пиков; в, г – общий вид при генерации n = 1600 данных для 2 и 8 пиков
 а
а 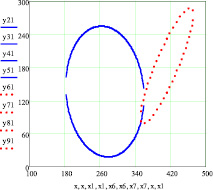 б
б
Рис. 2. Пересечение эллипсов распределения при задании по аналитическим выражениям: а – общий вид для 2 пика; б – общий вид для 8 пика
Пересечения эллипсов распределения по рис. 1 определяются вручную с подбором количества сгенерированных данных. По рис. 2 – также вручную при подборе обобщенного параметра кривизны эллипса R с использованием аналитических выражений.
Для автоматического выявления пересечения необходимо решить систему векторно-матричных аналитических уравнений, и это даст координаты точки пересечения. В данной работе рассматривается система только двух векторно-матричных уравнений
R2 = XT•Σ–1•X.
Аналитическую оценку пересечения эллипсов распределений предложено производить по решению системы векторно-матричных уравнений с нахождением координат точки пересечения в программе MathCad Edition 14. Реализованное решение в общем виде с использованием встроенных функций математического редактора MathCad Edition 14 представлено выражением 1. При этом использованы следующие обозначения: rXY, rXYAg – корреляционные матрицы рамановских поляризационных спектров полиэфирных волокон без наночастиц серебра и с наночастицами серебра соответственно; MENX, MENXAg – математические ожидания интенсивности пиков спектров с поляризацией поперек волокон Х без наночастиц серебра и с наночастицами серебра соответственно; MENY, MENYAg математические ожидания интенсивности пиков спектров с поляризацией вдоль волокон Y без наночастиц серебра и с наночастицами серебра соответственно; σΔX, σΔXAg – средние квадратические отклонения интенсивности пиков спектров с поляризацией поперек волокон Х без наночастиц серебра и с наночастицами серебра соответственно; σΔY σΔYAg – средние квадратические отклонения интенсивности пиков спектров с поляризацией вдоль волокон Y без наночастиц серебра и с наночастицами серебра соответственно; i – номер пика спектрограммы.
R := 4.2 i := 2
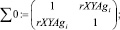
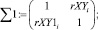
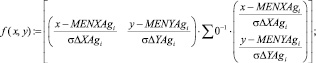
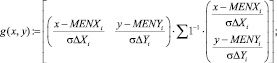 (1)
(1)
x: = 480.0 y: = 3500.0
Given
f(x, y) = 0 g(x, y) = 0
v: = Find(x, y)
Результаты исследования и их обсуждение
Решение системы векторно-матричных уравнений (1) для пика 1, представленное в виде цифровых результатов на рис. 3, а, производится по критерию пересечения эллипсов не в двух точках, а в одной для координат предельных значений ХV1(1) = 486.178811 и ХV1(2) = 486.178808 для RV1 = 2.6327965. Для двойного пересечения эллипсов распределения выявлена точка перехода из одного пересечения (только соприкосновение) RV1 = 2.6328692 ХV1 = 486.177701. Для координаты YV1(1) = 481.330075 и YV1(2) = 481.330068 для RV1 = 2.6327965 выявлено предельное значение пересечения. При начале двойного пересечения выявлена точка перехода из одной точки пересечения RV1 = 2.6328692 YV1 = 481.328982.
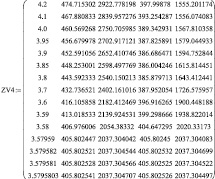
Решение системы векторно-матричных уравнений (1) для 4 пика показано на цифровых результатах на рис. 3, б. Координаты предельных значений ХV4(1) = 405.802541 и ХV4(2) = 405.802526 для RV4 = 3.5795803. Для двойного пересечения эллипсов распределения выявлена точка перехода из одного пересечения (только соприкосновение) RV4 = 3.57959 ХV4 = 405.802447. Для координаты YV4(1) = 2037.304707 и YV4(2) = 2037.304497 для RV4 = 3.5795803 выявлено предельное значение пересечения. При начале двойного пересечения выявлена точка перехода из одной точки пересечения RV4 = 3.57959 YV4 = 2037.0304042.
Для сопоставления предложенных методов проведем анализ полученных результатов.

а б
Рис. 3. Цифровые результаты решения системы аналитических уравнений: а – для 1 пика; б – для 4 пика
При векторно-матричном моделировании аналитического пересечения эллипсов распределения с решением системы уравнений получены координаты по 9 пикам:
для поперечной поляризации Х (ZV1i,1 и ZV1i,3)
XVnT = (486.179 192.216 267.413 405.802 474.453 566.051 654.178 349.533 697.074), (2)
для продольной поляризации Y (ZV1i,2 и ZV1i,4)
YVnT = (481.330 373.025 771.516 2037.30 2731.06 1061.18 1214.31 105.588 154.196), (3)
и эквивалентный радиус кривизны эллипсов при пересечении (ZV1i,0)
RVnT = (2.633 1.463 2.537 3.580 2.403 3.336 2.241 3.255 3.122). (4)
По сравнению с экспериментальными данными при моделировании с использованием генерации многомерных корреляционных зависимостей координаты пересечения эллипсов распределения следующие (по рис. 1):
для поперечной поляризации Х
XЭnT = (508.31 187.17 269.05 401.42 477.04 551.12 670.90 334.39 712.03), (5)
для продольной поляризации Y
YЭnT = (590.97 558.13 827.27 2005.9 2945.7 1138.8 1318.1 133.93 166.18). (6)
При выборе точек пересечения эллипсов распределения, построенных по математическим ожиданиям, средним квадратическим отклонениям, и коэффициентов корреляции с подбором эквивалентного радиуса эллипсов распределения получены координаты пересечения (по рис. 2):
для поперечной поляризации Х
XРnT = (488.20 192.22 267.37 409.82 474.45 565.68 654.19 349.52 697.07), (7)
для продольной поляризации Y
YРnT = (486.00 373.44 770.96 2095.7 2731.2 1059.1 1214.3 105.60 154.13), (8)
и эквивалентный радиус кривизны эллипсов при пересечении
RPnT = (2.636 1.463 2.538 3.584 2.403 3.335 2.241 3.255 3.122). (9)
Выводы
В работе предложен векторно-матричный метод моделирования эквивалентного радиуса эллипса распределения двухмерных корреляционных распределений при решении уравнений распознавания наночастиц коллоидного серебра на волокнах полиэфира по многомерным корреляционным составляющим рамановских спектров. Рассмотрены различные способы определения пересечения эллипсов распределения при распознавании наночастиц серебра на поверхности текстильных материалов. Выявлено, что наиболее близкое соответствие имеет место при оценках XVn, YVn, RVn по сравнению с экспериментальными XЭn, YЭn, где оценить эквивалентный радиус кривизны эллипсов не представилось возможным вообще.
При оценке достоверности идентификации наносеребра на волокнах полиэфира выявлены следующие значения для одномерных измерений по оси Х в поперечном направлении волокна:
для поперечной поляризации Х
pXT = (0.97917 0.92208 0.97917 0.99653 0.97917 0.99826 0.97917 0.98958 0.99479), (10)
для продольной поляризации Y
pYT = (0.78125 0.70833 0.77083 0.81250 0.77083 0.72917 0.79167 0.72917 0.87500). (11)
а при двухмерном измерении в поперечном Х и продольном Y направлениях с учетом коэфициентов корреляции:
pXYT = (0.9896 0.92708 0.99306 0.99935 0.98611 0.99826 0.97917 0.99653 0.99479). (12)
Таким образом, предложенный метод дает существенный выигрыш в оценке достоверности определения режимов нанесения наночастиц серебра на волокна. Например, для 4 пика увеличение произошло более чем в 1500 раз.



