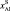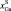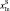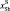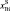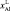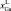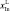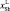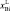Твердые растворы (ТР) полупроводниковых соединений на основе антимонида индия привлекательны в качестве материалов оптоэлектроники для работы в ИК-диапазоне. Однако практическое получение структур на основе этих ТР сопряжено с рядом технологических трудностей, обусловленных структурным и термодинамическим несоответствием наращиваемых эпитаксиальных слоев и подложки InSb [7, 6]. Использование висмута в расплаве гетеросистем А3В5 во многих случаях позволяет уменьшить плотность дефектов, обусловленных отклонением от стехиометрии, и повысить морфологическую устойчивость фронта кристаллизации [5].
В настоящей работе исследуются особенности температурных полей, в которых формируются пятикомпонентные гетероструктуры AlGaInSbBi и GaInAsSbBi на подложках InSb в поле температурного градиента. Этот метод обладает рядом преимуществ [4], однако воспроизводимость экспериментов крайне чувствительна к факторам, обусловливающим деградацию подложечного материала. С целью определения величин переохлаждения (dТ), минимально необходимых для подавления подрастворения подложек InSb, были проведены предварительные расчетные и экспериментальные исследования физических процессов, протекающих на межфазной границе.
Термодинамические процессы на фронте кристаллизации описывались, согласно [4], на основе уравнений гетерогенного равновесия [4] и обобщенного уравнения массопереноса:
(*)
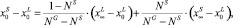где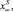 
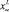– составы подложки и исходной жидкой фазы соответственно;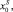 
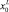– составы установившейся концентрации компонентов в обеих фазах; NS, NG – количество осевшей твердой и растворившейся жидкой фаз.
Расчет гетерогенных равновесий проводился по модели Онабэ [4]. Данные для расчетов были взяты из [6, 4, 1]. Недостающие параметры взаимодействия в твердой (αS) и жидкой (aL) фазах рассчитывали по модели регулярных растворов (aL) и ДПР-модели (αS) [2], при этом учитывались периодические свойства гомологических рядов, в которые входят компоненты системы.
В результате совместного решения уравнений гетерогенного равновесия [4] и баланса масс на границе раздела (*) находили глубину растворения подложки h = NGL, где L – толщина расплава и контактное переохлаждение, которое характеризуется равновесным переохлаждением жидкой фазы ΔTk. Для оценки ΔTk использовалась линейная аппроксимация фазовой диаграммы:
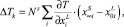
где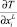 
– производная от температуры ликвидуса по соответствующему компоненту.
Задача решалась при следующих параметрах: температура контакта слоя и подложки – Тк1 = 684 К, Тк2 = 738 К; L = 250 мкм; δa = 0,005 нм.
Результаты расчетов приведены на рис. 1, 2. Анализ расчетных величин переохлаждения для кристаллизации на подложках InSb позволяет сделать следующие выводы. С увеличением содержания алюминия в твердой фазе DТ возрастает (рис. 1, кривая 4). Величина DТ при понижении температуры роста эпитаксиальных слоев (ЭС) заметно уменьшается (кривые 1, 2). Это свидетельствует о том, что химическая составляющая избыточной свободной энергии в рассматриваемых процессах взаимодействия фаз играет существенную роль. Расчетные величины переохлаждения, необходимые для подавления подрастворения подложек из InSb (111), на ≈ 1,5–1,8 K меньше, чем для подложек InSb (100) (кривые 1, 3).
Полученные результаты можно объяснить ориентационным эффектом, характерным для большинства бинарных подложек типа А3В5 [6]. Для ТР на основе антимонида индия расчетные величины ΔТ лежат в диапазоне 9–12 К. При выращивании ЭС в поле температурного градиента реальные значения ΔТ могут достигать 14 К и более. При более высоких значениях величины ΔТ может реализоваться объемная кристаллизация в растворе-расплаве [4]. Поэтому для составов с DТ > 14 К необходимо обеспечить дополнительную защиту подложек от подрастворения. Это можно сделать, например, путем выращивания буферных слоев [1].
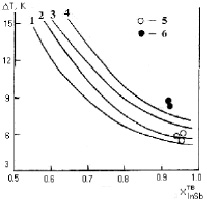
Рис. 1. Расчетная зависимость исходного переохлаждения раствора-расплава от состава жидкой фазы (Al, Ga, In, Sb, Bi), выраженного через состав равновесного твердого раствора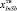 
: 1 – составы при ТК = 673К, ориентация подложки InSb (111), содержание Al в твердой фазе 
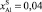; 2 – ТК = 723К, InSb (111), 
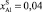; 3 – ТК = 723К, InSb (100), 
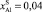; 4 – ТК = 723К, InSb (100), 
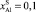. (точки – экспериментально определенные значения ΔТ, где при 5 – ΔТ, tЛИКВ = 684К; 6 – DТ при tЛИКВ = 738 К)
Экспериментальные точки смещены в сторону более высоких температур относительно расчетных данных на 1,5–2 К. Это, по-видимому, обусловлено недостатками моделей, используемых для расчета гетерогенных равновесий. Экспериментальные данные были получены путем кратковременного, в течение 15 секунд, совмещения жидкой и твердой фаз соответствующего состава с последующим микроскопическим анализом подложки. В проведенной серии экспериментов величина температуры контакта фаз (tK) уменьшалась с шагом в один градус от температуры ликвидуса (tЛИКВ) до тех пор, пока на поверхности подложки оставались следы растворения. Величина переохлаждения определялась согласно формуле
ΔТ = tЛИКВ – tK.
Расчетные данные по составам жидкой и твердой фаз гетероструктуры AlхGaуIn1-х-у Sb<Bi>
|
№ п/п |
|
|
|
|
|
|
|
|
|
|
Тр, К |
|
1 |
0,1 |
0,89 |
0,01 |
0,99 |
0,01 |
0,01 |
0,11 |
0,09 |
0,46 |
0,33 |
684 |
|
2 |
0,04 |
0,08 |
0,88 |
0,986 |
0,014 |
0,025 |
0,13 |
0,18 |
0,43 |
0,235 |
738 |
Расчет проводился для температур ликвидуса 684 К и 738 К и составов, приведенных в таблице. Составы и tЛИКВ рассчитывали по методике [4].
На рис. 2 показана расчетная зависимость изменения величины переохлаждения от различия параметров решетки подложки и растущего эпитаксиального слоя.
Для роста растянутых ЭС требуются меньшие величины ΔТ, чем для ЭС, подверженных сжатию. Это объясняется более высоким энергетическим вкладом, вносимым упругими напряжениями сжатия. Кривая отклонения δТ скорректирована с учетом экспериментальных значений.
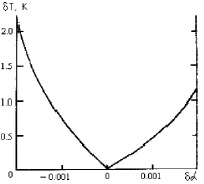
Рис. 2. Зависимость изменения переохлаждения dТ от величины упругих напряжений на гетерогранице
Максимальное отклонение δТ составляет 2,3 К при величине δа = –0,002, то есть структурное несоответствие растущего ЭС подложке значительно влияет на ΔТ и, следовательно, на качество получаемых гетероструктур.
Еще одним важным лимитирующим фактором является ограничение по плавкости, суть которого заключается в существовании интервала составов твердых фаз, для которых невозможно определить равновесные жидкие фазы (при температурах выше температуры самого легкоплавкого компонента, входящего в ТР). Причиной являются низкие значения температуры плавления антимонидов индия (798 К) и галлия (983 К). Как показали исследования, проведенные в лаборатории физики полупроводников и в Санкт-Петербургском государственном электротехническом университете ЛЭТИ, для четырех- и пятикомпонентных систем соответствующее ограничение наступает при пересечении изотермой солидуса линии, соответствующей стехиометрическому составу жидкой фазы, при котором термодинамические функции системы проходят через экстремум [3]. Необходимо отметить, что в системах А3В5, содержащих висмут, ограничения по плавкости особенно существенны и их следствием является резкое сужение областей составов твердых растворов, доступных для получения методами эпитаксии из жидкой фазы, в том числе и ГЖЭ. Проведенный анализ показал, что в антимонидных висмутсодержащих системах возможно получение твердых растворов с низким содержанием компонентов, не входящих в состав подложек (InSb, GaSb), так, для систем GaxIn1-xAszSb1-y-z Biy/InSb содержание висмута не превышает 5 ат. %.
Рассмотрим контакт n-компонентного твердого раствора (концентрации компонентов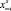 
) с неравновесным жидким расплавом 
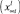. Пусть в результате контакта некоторое количество вещества твердой фазы перешло в расплав. Обозначим количество растворившегося вещества через NS, а число компонентов в системе – n. Тогда на стадии растворения подложки перераспределение компонентов между взаимодействующими фазами приведет к установлению в растворе концентрации 
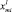i-го компонента, подчиняющейся следующему уравнению массового баланса:
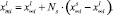
Равновесный распад NG пересыщенной жидкой фазы, сопровождающийся выделением твердого раствора состава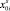 
, равновесного жидкому раствору расплаву 
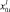, может быть представлен в виде
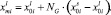
Приходим к следующему обобщенному уравнению массопереноса:
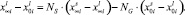
Соотношение между растворенным и кристаллизовавшимся количеством вещества удобно оценить параметром
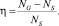
Таким образом, задавая типичные значения NS и решая совместно n уравнений и (n – 1) уравнений, описывающих фазовые равновесия [2], находим величину NG – количество кристаллизовавшегося вещества, а следовательно, и параметр h. Очевидно, что положительному значению h соответствует устойчивое состояние подложки в расплаве, при h < 0 будет происходить растворение подложки.
Для оценки устойчивости контактирующих фаз проводился расчет критерия h применительно к контактам расплавов GaSbBi с подложками GаSb, GaAsP <Bi> с подложками GаP и InSbBi с InSb. Результаты расчетов для последней гетеросистемы приведены на рис. 3. Установлено, что оптимальные температурные режимы для рассматриваемых систем составляют: GaSb <Bi> /GaSb – 830–883 K; GaAsP <Bi> /GaP, – 1253–1290 K; InSbBi/InSb – 673–693 K.
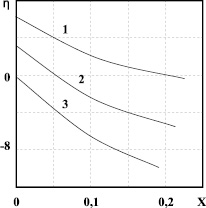
Рис. 3. Зависимости h от состава и температуры в ТР InSb1-XBiX/InSb: 1 – T = 650 K; 2 – T = 690K; 3 – T = 710 K
Подобный анализ для других висмутсодержащих гетероструктур показал аналогичную зависимость h от состава и Т. Отметим, что указанный анализ особенно важен при создании условий самоорганизации, когда для создания поля незатухающих флуктуаций температура, как правило, выбирается максимальной из всего допустимого диапазона.
Таким образом, сопоставление расчетной зависимости величин переохлаждения от состава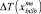 
и экспериментальных данных показало, что в реальных условиях градиентной кристаллизации существуют ограничения по составу ЭС AlхGaуIn1-х-уSb<Bi> и GaxIn1-xAszSb1-y-z Biy/InSb, которые можно вырастить непосредственно на подложке InSb. Для получения твердых растворов с большими значениями х следует использовать прием предварительного выращивания на подложке буферных слоев, позволяющих уменьшить ΔТ. Результаты расчетов могут служить основой для разработки температурно-временных режимов получения Bi-содержащих твердых растворов, обеспечивающих их воспроизводимое получение в поле температурного градиента.