Тема энергоэффективности Российской экономики на протяжении уже длительного времени является актуальной. Работы над повышением этого показателя ведутся в разных областях: принимаются законы, тарифы, исследуются новые материалы и технологии. Одной из отраслей, которые, по мнению исследователей, обладают значительным потенциалом энергосбережения, является ЖКХ [1].
Среди шагов, предпринимаемых в направлении повышения эффективности потребления энергии многоквартирными домами, действенным и важным является установка систем АСКУЭ. В то же время необходимо понимать, что организация достоверного и оперативного учета энергопотребления сама по себе не является залогом успеха. Применение АСКУЭ для коммерческого учета расхода электроэнергии в МКД, конечно же, удобно для энергосбытовых компаний, управляющих компаний и добросовестных конечных потребителей. В то же время, большой объем данных, который агрегируют АСКУЭ, по мнению автора, может быть использован для анализа с целью выявления закономерностей и правил, которые могут обеспечить информационно-аналитическую поддержку мер повышения энергоэффективности многоквартирных домов.
Другой важной мерой является составление энергетических паспортов зданий и определение классов энергетической эффективности объектов. Вне сомнений, такой энергоаудит мог бы значительно прояснить реальную картину, помочь определить многоквартирные дома, которые в первую очередь нуждаются в принятии мер по повышению энергоэффективности. Однако необходимо учесть, что полноценный энергоаудит – достаточно дорогостоящая операция, и ее проведение даже в масштабах среднего города, не говоря уже о городах-миллионниках, может стоить бюджету значительных сумм. Так, по сообщениям дирекции коммунального хозяйства и благоустройства г. Саранска, сделанным в 2011 году, в ближайшей (на тот момент) перспективе на фасадах всех многоэтажных зданий должны были появиться таблички с указанием класса энергетической эффективности. На момент проведения данного исследования (начало 2016 года) такие таблички установлены не были [3]. Это может подтверждать тезис о том, что проведение полноценного энергоаудита в масштабах целого города – сложная и дорогостоящая процедура.
Более оптимальным и гораздо менее дорогостоящим решением, пригодным для первичной оценки ситуации, изучения общей картины в масштабах района или города, может стать проведение процедуры бенчмаркинга. Бенчмаркинг – практика сравнения измеренной фактической производительности устройства, процесса, объекта или организации по отношению к своим более ранним состояниям, аналогичным объектам или установленным нормам с целью информирования и мотивации к повышению производительности [2]. В контексте задачи повышения энергоэффективности жилого сектора российских городов бенчмаркинг – процедура количественного определения потенциала энергосбережения многоквартирных жилых домов, а также ранжирования некоторого множества таких домов на основе совокупности выявленных значений.
Процедура бенчмаркинга требует определения некоторых индикаторов потенциала энергосбережения как максимально инвариантных к внешним условиям величин. Прежде всего, исследователи стремятся некоторым способом исключить зависимость величины потребляемой электроэнергии от площади жилья (корреляция между этими величинами очевидна). Как следствие, в рамках исследований часто анализируется удельная величина, такая как кВт•ч/м2, или же кВт•ч/фут2. Данную величину в зарубежных исследованиях называют Energy Use Intensity (EUI), или Интенсивность Энергопользования. При проведении исследований, как правило, считается, что объем потребляемой энергии линейно зависит от площади изучаемого объекта (будь то жилое или коммерческое здание) [4]. Действительная же ситуация, по мнению автора, может не соответствовать подобному утверждению. Этот тезис проиллюстрирован на рис. 1: данные, изображенные на левом графике только с большим трудом можно назвать линейно зависимыми. Кроме того, изображение справа свидетельствует о возможном наличии связи между площадью дома и средним потреблением в отдельных квартирах, чего при линейной зависимости суммарного потребленного объема энергии в доме от общей площади наблюдаться не должно.
Применение столь простого индикатора, как EUI, по мнению ряда исследователей, является достаточно спорным приемом, поэтому зачастую также учитывается влияние метеофакторов: вычисление показателей для зданий на основе значений, собранных при разных погодных условиях, может привести к неправильным выводам. Для коммерческих зданий важно учитывать часы работы.
Моделирование величины потребляемой электроэнергии – один из эффективных способов информационно-аналитической поддержки мер повышения энергоэффективности многоквартирных жилых домов. Несмотря на заметное внимание к проблемам энергосбережения в различных отраслях российской экономики, меры статистического наблюдения за уровнями эффективности использования энергии в жилых домах на сегодняшний день не получили должного распространения [1]. В то же время многие зарубежные ученые уделяют значительное внимание упомянутым моделям в своих исследованиях.
Согласно [9], модели потребления электроэнергии могут быть отнесены к двум категориям: нисходящие модели и восходящие. Первые исследуют особенности потребления энергии в рамках целых регионов и влияние на эту величину общих макроэкономических показателей, таких как ВВП. Вторые ставят объектом своих исследований конечных потребителей – отдельные домовладения или же многоквартирные дома. В рамках восходящих моделей, в свою очередь, выделяют инженерные и статистические методы. Инженерные методы базируются прежде всего на данных технического характера, описывающих исследуемые объекты, т.е. строения. Статистические методы используют, помимо прочего, исторические данные о потреблении электроэнергии.
Задачу моделирования величины потребляемой энергии можно представить следующим образом:
Заданы временные ряды, состоящие из матрицы признаков Х (где xij представляет собой вектор значений j-х признаков в день t для объекта учета, в котором установлен i-й прибор учета) и измеренных значений потребленной электроэнергии yi(t)∈R – показания i-го прибора учета за день t (i∈I, I – множество приборов учета, t∈N – натуральное число). Требуется восстановить регрессионную зависимость y = f(X).
Используемая модель, с точки зрения дисперсионного анализа, может быть представлена в следующем виде:
(Наблюдаемое значение) = Σ[Параметры, описывающие определяемые эффекты] + Σ[Случайные величины, описывающие неопределяемые (остаточные)эффекты].
С учетом особенностей предметной области, мы можем заметить, что случайные величины, описывающие остаточные эффекты, в общем могут быть отнесены к двум группам: не известные нам в процессе факторы, характеризующие конструктивные особенности здания, и факторы, описывающие особенности потребления энергии жильцами МКД (т.е. конкретными людьми, имеющими свои привычки, потребности и возможности, во многом определяющие общую картину).
Самым простым, но в то же время получившим широкое распространение подходом стала линейная регрессия вида:
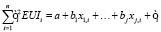 ,
,
где x(j, i) – факторы, влияющие на моделируемую величину, a и b – некоторые коэффициенты, ε – случайная ошибка [8]. В рамках данного метода также делается предположение о линейной зависимости EUI от исследуемых факторов, однако в реальных данных зависимость может иметь другой вид, что проиллюстрировано рис. 1.
Описаны способы построения регрессионных моделей энергопотребления на основе методов машинного обучения [8]. Целесообразность их применения к данной задаче обусловлена нелинейной зависимостью между регрессорами и переменной отклика, а также наличием других сложных и неочевидных взаимосвязей в данных.
Следует отметить, что построение регрессионной модели как таковой не является конечной целью анализа – выводы позволяет делать исследование остатков:
εi = yi – fi,
где fi – отклики, посчитанные по модели, yi – эмпирические остатки [10]. На основе анализа величин остатков для различных зданий производится процедура кластеризации, в конечном итоге определяющая каждое из зданий в некоторую группу. Каждая группа характеризуется оценкой (от неудовлетворительной до отличной), позволяющей сделать вывод о потенциале энергосбережения данного строения.
Предложенные Джеромом Фридманом многомерные адаптивные регрессионные сплайны (MARS) [6] обладают рядом преимуществ перед другими регрессионными методами:
- модели MARS – более гибкие, нежели модели, построенные при помощи линейной регрессии;
- модели MARS являются более простыми для понимания, их результаты проще интерпретировать (по сравнению, например, с нейронными сетями или SVM);
- MARS позволяет работать с численными и категориальными признаками;
- благодаря разделению исходных данных на области базисными функциями, MARS позволяет определять выбросы;
- кусочно-линейные базисные функции с узлом в некоторой точке, применяемые в MARS, позволяют лучше аппроксимировать численные переменные по сравнению с кусочно-константными функциями, используемыми в регрессионных деревьях;
- MARS не требует значительных мер по подготовке входных данных;
- для моделей MARS, как правило, характерен оптимальный баланс смещения/дисперсии (bias-variance tradeoff).
Перечисленные преимущества являются существенными для проведения энергетического бенчмаркинга, требующего учета большого числа разнородных факторов.
MARS относится к разряду непараметрических процедур (в противоположность параметрическим, таким, как например, линейная регрессия). Параметрический подход заключается в предположении, что функция отклика Y имеет некоторую предписанную функциональную форму. Непараметрические процедуры в свою очередь подразумевают использование модели, не описываемой конечным числом параметров. Несмотря на то, что параметрические методы просты в плане построения и интерпретации результатов, их «гибкость» бывает зачастую недостаточной при решении реальных задач. Для того, чтобы справиться с этой проблемой, используют подход, при котором непараметрические аппроксимирующие функции строятся отдельно на некоторых областях исходных данных. При этом сначала решается задача нахождения оптимального числа таких областей (в русскоязычной литературе их иногда называют гильотинными разбиениями).
Одним из известных непараметрических подходов является рекурсивная разделяющая регрессия (Recursive partitioning regression, RPR). RPR – адаптивный алгоритм построения аппроксимирующей функции, позволяющий работать с большим числом регрессоров.
Пусть дан некоторый набор регрессоров X = {x1, x2,…, xn}, определенный в пространстве 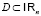 , зависимая переменная y, а также ряд из N наблюдений
, зависимая переменная y, а также ряд из N наблюдений 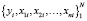 . Фактическая взаимосвязь между y и X может быть выражена следующей формулой:
. Фактическая взаимосвязь между y и X может быть выражена следующей формулой:
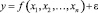 ,
,
где y – некоторая неизвестная функция, а ε – ошибка. RPR аппроксимирует f(x) следующим образом:
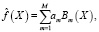 (1)
(1)
где 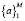 – коэффициенты модели, подобранные с целью максимального соответствия исходным данным. M – число областей, на которые разделен массив данных
– коэффициенты модели, подобранные с целью максимального соответствия исходным данным. M – число областей, на которые разделен массив данных 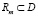 и в то же время число базисных функций Bm модели. Базисная функция определяется выражением
и в то же время число базисных функций Bm модели. Базисная функция определяется выражением
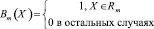
RPR является относительно мощным методом, при этом обладая рядом недостатков. Одним из них является наличие разрывов на границах разбиений. Многомерные адаптивные регрессионные сплайны представляют собой обобщение RPR, позволяющее избежать многих ограничений последнего. В основе метода MARS лежат кусочно-линейные базисные функции (получившие в западной литературе название «hockey stick», благодаря форме графика), отражающие связь между x и х*:
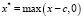 , (2)
, (2)
где c называют узлом базисной функции. Отметим, что подобным образом может быть использована функция
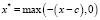 , (3)
, (3)
график которой зеркально отражен по сравнению с графиком функции (2). Пример подобного графика представлен на рис. 2.
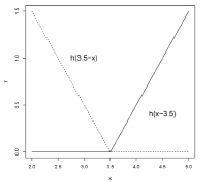
Рис. 2. Пример графика hinge-функции
Метод многомерных адаптивных регрессионных сплайнов видоизменяет модель (1), представляя её в следующем виде:
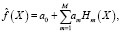
где Hm (X) – базисные функции, задаваемые выражением
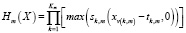 .
.
Здесь v(k, m) – регрессоры, соответствующие базисной функции Hm, Km – степень взаимодействия между переменными v(k, m), tk,m задает местоположение узла функции Hm, а sk,m – коэффициент принимающий значения – 1 и + 1 и задающий форму базисной функции (2) или (3). Метод MARS осуществляет построение модели в два этапа: прямая шаговая и обратная шаговая регрессии. На первом этапе (прямая шаговая регрессия) вся выборка D разделяется на ряд областей, для каждой из которых производится подбор параметров модели. Если число таких областей не задано, то на этом этапе мы получим по одной базисной функции для каждого значения. Кроме того, придется учитывать все возможные взаимосвязи между регрессорами [11].
На втором этапе отбрасываются те из базисных функций, которые меньше всего влияют на точность модели. Для того, чтобы обеспечить приемлемое время работы алгоритма, степень взаимодействия между регрессорами и максимальное количество базисных функций предлагается задавать пользователю.
Для оценки обобщающей способности алгоритма MARS используется критерий кросс-проверки (MGCV):
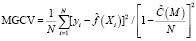 ,
,
где 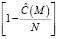 – штраф, учитывающий изменение дисперсии значений, а
– штраф, учитывающий изменение дисперсии значений, а 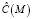 определяется следующим образом:
определяется следующим образом:
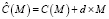 .
.
Здесь C(M) – число параметров модели, а d – еще один штраф, значение которого, как правило принимают равным 3 [11].
Методу MARS свойственны некоторые недостатки:
- по сравнению с MARS, регрессионные деревья обладают значительным преимуществом в скорости;
- как и для других методов непараметрической регрессии, для MARS не представляется возможным непосредственно определить значения доверительных интервалов параметров (в отличии от линейной регрессии), и для проверки модели приходится использовать кросс-валидацию;
- модели MARS не обеспечивают столь же качественного приближения данных, как деревья решений, построенные методом градиентного роста, однако их построение занимает значительно меньшее время, а результаты проще интерпретировать;
- открытые программные реализации MARS (такие, как, например, пакет earth для языка R) не позволяют обучать модели на основе данных, содержащих пропущенные значения, в то же время регрессионные деревья могут быть использованы для решения подобной задачи.
Следует заметить, что подготовка данных (включающая очистку и замещение пропущенных значений [3]), подбор наиболее оптимальных гиперпараметров для MARS-моделей, а также осуществление перекрестной проверки могут позволить существенно уменьшить влияние недостатков выбранного метода на процедуру моделирования и конечный результат. Именно этой задаче и посвящена данная работа.
Для обучения MARS-моделей в рамках данного исследования был использован набор данных о многоквартирных домах г. Саранска в совокупности с историей показаний автоматизированной системы коммерческого учета потребления энергоресурсов (АСКУПЭ) и сведениями, характеризующими температуру воздуха и длину светового дня на рассматриваемых временных отрезках. Отдельно следует упомянуть, что данные организованы иерархически: некоторые признаки соответствуют уровню дома (например дата постройки или тип кровли), другие – уровню квартиры (средний возраст проживающих, наличие льгот и т.д.), отдельные признаки определены для всего множества исследуемых объектов, то есть для целого города (среднесуточная температура, длительность светового дня). Для обучения были использованы следующие признаки.
Приборы АСКУПЭ фиксируют расход электрической энергии в квартирах дважды в сутки (днем и ночью), передавая значения на единый сервер при помощи ЛВС. Обрабатываемые значения представляют собой набор временных рядов y(ti), где ti∈R. К сожалению, как и для любых сложных технических систем, для АСКУЭ характерны ошибки. Грамотная эксплуатация и настройка системы позволяют минимизировать количество проблемных данных, однако не позволяют избежать их совсем. Использование ошибочных, некорректных сведений крайне нежелательно при проведении технического или коммерческого учета. Успех работы алгоритмов регрессионного анализа в то же время зависит от качества данных. При наличии большого числа ошибок наблюдения процедура восстановления аппроксимации неизвестной функции отклика может оказаться неуспешной, что не позволит сконцентрировать внимание на важных особенностях зависимости. Это обуславливает необходимость проведения операции очистки исходных данных.
Большинство зарубежных публикаций в качестве объектов исследований описывают или частные домовладения, или крупные коммерческие здания (офисы, торговые центры, моллы и т.д.). Отечественные урбанистические реалии значительно отличаются от зарубежных. Жилой фонд в городах нашей страны представлен преимущественно многоквартирными зданиями. Более того, по-прежнему не получили массового распространения системы кондиционирования (об изначально предусмотренных в зданиях системах говорить не приходится). Преимущественное использование центрального отопления также определяет иные паттерны потребления электроэнергии. Кроме того, многие особенности взаиморасчетов между потребителями и поставщиками абсолютно не характерны для развитых стран дальнего зарубежья (примером тому может служить распространенность льгот среди различных групп населения) [7]. Поэтому в рамках данного исследования впервые делается попытка применения статистических инструментов для изучения особенностей энергопотребления в МКД.
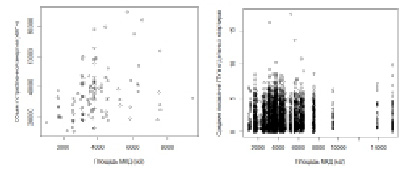
Рис. 1. Зависимость суммарного объема электроэнергии в исследуемой группе МКД от площади (на основе данных биллинговой системы и АСКУЭ для МКД г. Саранска)
Таблица 1
Список признаков, использованных для обучения модели
|
Признак |
Тип |
Возможные значения |
Псевдоним |
Уровень иерархии |
|
Площадь дома |
Вещественная |
8120, 5300, 4100 ... |
totalArea |
Дом |
|
Этаж |
Целочисленная |
1, 3, 10 ... |
Floor |
Квартира |
|
Площадь квартиры |
Вещественная |
42.0, 72.5, 101.1 ... |
area |
Квартира |
|
Количество проживающих |
Целочисленная |
0, 2, 5 ... |
residents |
Квартира |
|
Средний возраст проживающих |
Вещественная |
35.7, 78.3, 54.7 ... |
avgAge |
Квартира |
|
Время суток |
Категориальная |
День/Ночь |
timeOfDay |
Город |
|
Дата постройки здания |
Целочисленная |
1974, 1982, 2001 ... |
yearBegin |
Дом |
|
Среднесуточная температура |
Целочисленная |
+ 3, – 20, 0 ... |
avgTemp |
Город |
|
Продолжительность светового дня |
Целочисленная |
9, 8, 11... |
dayLength |
Город |
|
Тип кровли |
Категориальная |
Металлическая Мягкая Шатровая Шифер Безрулонная |
roofType |
Дом |
|
Тип фундамента |
Категориальная |
Бетонный ленточный Бутовый Бутовый ленточный Железобетонный Железобетонные блоки Керамзитобетонные блоки Сборный ж/б |
foundationType |
Дом |
|
Тип отопления |
Категориальная |
Централизованное Автономное |
heatingType |
Дом |
|
Тип стен |
Категориальная |
Кирпичные Панельные Сборный железобетон Монолитные |
wallType |
Дом |
|
Широта |
Вещественная |
54.11 |
attitude |
Дом |
|
Долгота |
Вещественная |
45.11 |
longitude |
Дом |
|
Выходной или праздничный день |
Булева |
TRUE, FALSE |
weekend |
Город |
|
Тип оборудования, используемого для обогрева пищи |
Категориальная |
Электроплиты, газовые плиты |
eqType |
Дом |
|
Наличие льгот на оплату электроэнергии у проживающих |
Булева |
TRUE, FALSE |
isBenefit |
Квартира |
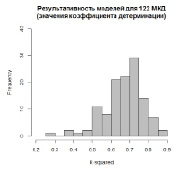
Рис. 3. Распределение значений RSS восходящих моделей MARS уровня дома (максимальная степень взаимодействия D = 1)
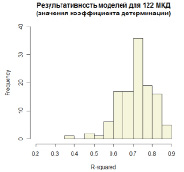
Рис. 4. Распределение значений RSS восходящих моделей MARS уровня дома (максимальная степень взаимодействия D = 2)
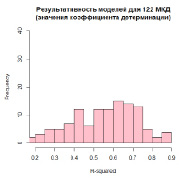
Рис. 5. Распределение значений RSS для восходящих моделей MARS уровня дома (максимальная степень взаимодействия D = 5)
Исходные данные, как упоминалось выше, детализированы на уровнях квартир и домов. На начальном этапе для каждого многоквартирного дома была построена отдельная модель уровня квартиры (т.е. позволяющая оценивать значения потребляемой электроэнергии в квартире с заданными параметрами).
Целями вычислительных экспериментов являются:
1. Исследование возможности применения MARS в задачах моделирования энергопотребления и энергетического бенчмаркинга.
2. Выявление наиболее оптимальных гиперпараметров для MARS-моделей.
3. Определения наиболее значимых факторов, влияющих на моделируемую величину (на основе совокупности данных о множестве МКД г. Саранска).
Ряд гиперпараметров MARS-моделей задается пользователем. Среди них – пороговое значение RSS, при котором завершается первый проход алгоритма, некоторые характеристики процедуры автоматической кросс-валидации, а также максимальная степень взаимодействия различных переменных в рамках одной базис-функции (иными словами, максимальное число переменных, которые могут быть задействованы в одной базисной функции). Последний параметр позволяет сделать некоторые выводы о природе данных, в частности, о взаимосвязи некоторых регрессоров.
Распределение значений коэффициента детерминации
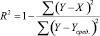
для таких моделей со значением параметра максимальной степени взаимодействия D, равным 1, представлено на рис. 3. Распределение для значений D = 2 и D = 5 отображено соответственно на рис. 4 и 5.
Сравнение распределений коэффициентов детерминации для моделей с различными значениями D показывает, что значение зависимой переменной лучше всего определяется при условии вхождения максимум двух членов с различными регрессорами в одну базисную функцию.
Профили суммарного удельного объема потребленной электроэнергии двух МКД, модели которых имеют соответственно лучший (> 0,9) и худший (< 0,4) коэффициенты детерминации представлены на рис. 6, а и б.
Алгоритм MARS позволяет определять степень влияния различных факторов на переменную отклика [6]. Для этого могут быть использованы три оценки.
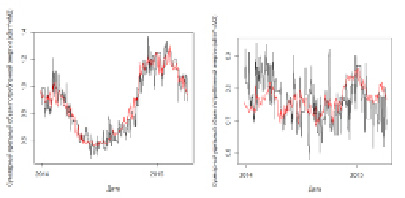
Рис. 6. Смоделированные (светлая линия) и эмпирические (темная линия) профили суммарного удельного объема потребленной электроэнергии. Модели, показавшие результаты R2 > 0,9 (а) и R2 > 0,4 (б) (D = 2). https://www.youtube.com/watch?v=17QbQF__9XM
Таблица 2
Оценки значимости самых важных регрессоров для четырех моделей с разными коэффициентами детерминации (D = 2)
|
№ модели |
Размерность |
R2 |
Регрессор «Residents» (число зарегистрированных жильцов) |
Регрессор «AvgAge» (средний возраст жильцов) |
Регрессор «IsBenefit» (Наличие льгот) |
Регрессор «DayLength» (Длина светового дня) |
Регрессор «T» (Средняя дневная температура) |
||||||||||
|
Тип оценки |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
||
|
10 |
30 |
0,74 |
20 |
45,2 |
45,4 |
27 |
100 |
100 |
17 |
33,8 |
34,0 |
12 |
20,7 |
21,1 |
– |
– |
– |
|
51 |
37 |
0,62 |
29 |
58,8 |
59,5 |
31 |
100 |
100 |
28 |
58,6 |
59,2 |
20 |
25,9 |
27,3 |
17 |
21,2 |
22,7 |
|
84 |
38 |
0,59 |
33 |
100 |
100 |
30 |
93,8 |
93,7 |
31 |
96,4 |
96,3 |
30 |
89,2 |
89,5 |
23 |
43,0 |
44,2 |
|
120 |
15 |
0,46 |
10 |
53,6 |
54,1 |
13 |
100 |
100 |
– |
– |
– |
5 |
13,8 |
15,4 |
3 |
7,5 |
9,3 |
Первая основывается на подсчете числа вхождений переменной в подмножества Si множества базисных функций, конструируемого на втором (обратном) этапе работы алгоритма. Такие подмножества имеют мощность 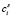 , где i изменяется в пределах 1 до n, а n – размерность итоговой модели. Для каждого i подмножество S – наилучшее (с точки зрения приближения функции) из всех возможных подмножеств данной мощности.
, где i изменяется в пределах 1 до n, а n – размерность итоговой модели. Для каждого i подмножество S – наилучшее (с точки зрения приближения функции) из всех возможных подмножеств данной мощности.
RSS-оценка вычисляется следующим образом: сначала определяется величина, на которую уменьшает показатель RSS каждое из подмножеств Si. Затем эти величины суммируются на всех подмножествах, включающих нужную переменную.
GCV-оценка работает схожим образом, за исключеним того, что вместо суммы квадратов остатков вычисляется упомянутый выше обобщенный критерий кросс-проверки.
Все три оценки для простоты интерпретации их значений масштабируют в интервале [1, 100]. Примеры значений описанных оценок для ряда моделей представлены в табл. 2, где для каждого из пяти самых значимых регрессоров («Residents», «AvgAge», «IsBenefit», «DayLength», «T») в колонках «1», «2» и «3» указаны значения соответствующих оценок.
Отдельный интерес представляют факторы уровня МКД. Для изучения их влияния на зависимую переменную (измеряемую в кВт•ч/м2) построена MARS-модель, основанная на агрегированных данных. Значение R2 для данной модели составило 0,52. В табл. 3 представлены оценки значимости факторов (каждая из трех описанных оценок для каждого из регрессоров указана в соответствующем столбце «1», «2» и «3»).
Таблица 3
Оценки значимости самых важных регрессоров для модели уровня МКД
|
Оценки |
|||
|
Регрессоры |
1 |
2 |
3 |
|
floor (Этажность) |
31 |
100,0 |
100,0 |
|
houseAge (Год постройки) |
30 |
91,3 |
91,3 |
|
attitude (Координаты широты) |
28 |
89,7 |
89,7 |
|
longitude (Координаты долготы) |
28 |
81,9 |
81,9 |
|
numberOfBenefits (Процент льготников среди жильцов) |
18 |
54,8 |
54,8 |
|
roofType (Тип крыши) |
13 |
42,2 |
42,2 |
|
avgAge (Средний возраст жильцов) |
8 |
20,7 |
20,8 |
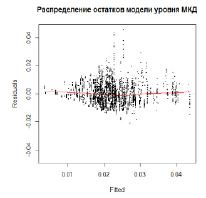
Рис. 7. Распределение остатков модели уровня МКД
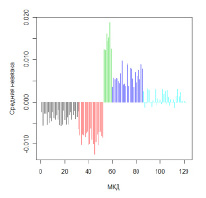
Рис. 8. Кластеризация 122 МКД на основе сведений о средних невязках
Из рис. 7, отражающего распределение остатков построенной модели, можно сделать выводы о гетероскедатичности модели. В то же время следует отметить, что важными критериями качества моделей многомерных регрессионных сплайнов являются прежде всего независимость остатков и их симметричность.
Для наглядной интерпретации модели представляется возможным осуществить кластеризацию остатков при помощи метода k-средних, который стремится минимизировать суммарное квадратичное отклонение точек кластеров от центров этих кластеров:
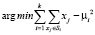 ,
,
где k – число кластеров, Si – полученные кластеры, i = 1, 2, 3,…, k и μi – центры масс векторов xj∈Si.
Результат проведения данной операции (при k = 5) представлен на рис. 8. Каждому МКД соответствует отдельный столбец. Дома, принадлежащие разным кластерам, отмечены различными цветами (и упорядочены по индексу кластера). На оси ординат отражена средняя невязка, полученная в результате применения описанной выше регрессионной модели. Каждому из полученных кластеров можно дать некоторую относительную оценку, характеризующую ситуацию с эффективностью использования электроэнергии: от «неудовлетворительно» (черные столбцы на графике) до «отлично» (зеленые столбцы).
Выводы
В рамках данной работы было проведено исследование свойств моделей энергопотребления на основе многомерных адаптивных регрессионных сплайнов. Были построены модели различного уровня, использующие в основе данные разной степени детализации. Выявлены факторы, которые наиболее значительно среди прочих исследованных влияют на моделируемую величину удельного энергопотребления на уровне квартиры и уровне многоквартирного дома, а также экспериментально установлено наличие взаимосвязей между регрессорами.
Среди факторов уровня МКД наиболее значимыми оказались этажность, год постройки, координаты (широта и долгота), процент льготников среди жильцов, тип крыши, средний возраст жильцов, среди факторов уровня квартир – число зарегистрированных жильцов, средний возраст, наличие льгот, а также длина светового дня и среднесуточная температура.
Наилучшим образом аппроксимируют данные модели, для которых значение максимальной степени взаимодействия регрессоров D = 2. Значения коэффициента детерминации R2 для моделей уровня квартиры в среднем составили 0,716. Значение R2 для модели уровня дома составило 0,52.
Предложен способ проведения первичного энергоаудита, основанный на статистическом анализе данных. Преимуществом данного способа является высокая степень независимости результатов от часто меняющихся факторов, таких как длина светового дня, средний возраст жильцов или среднесуточная температура. Результаты такой процедуры могут стать основой для принятия решения о необходимости детального обследования тех или иных многоквартирных зданий.
В целом результаты данного исследования позволяют сделать вывод о целесообразности применения многомерных адаптивных регрессионных сплайнов для анализа данных об энергопотреблении в МКД.



