Электротермический способ производства фосфора удовлетворяет основным необходимым требованиям, таким как высокая температура, восстановительная среда, высокая чистота продукта и т.д., поэтому этот способ вполне конкурентоспособен с химическими методами. Процессы химической электротермии весьма энергоемки, причем около 80–85 % в общих затратах занимает электроэнергия для питания электротермических печей и привода силового оборудования.
В зависимости от способа термической подготовки фосфоритного сырья затраты энергии могут быть различными. Например, для кускового фосфорита и агломерата удельный расход электроэнергии в печи 14,8 МВт×/т (РКЗ-72Ф) и 14,2 МВт×ч/т (РКЗ-80Ф) соответственно, затраты электроэнергии на привод силовых установок 1,411 и 2,477 МВт×ч/т, расход условного топлива на подготовку сырья 0,31 и 1,93 ТУТ/т, расход восстановителя в печах 2,34 и 1,55 ТУТ/т.
Затраты энергии увеличиваются при переработке фосфоритовой мелочи в фосмуку для получения окатышей. В настоящее время применяются три основные технологические схемы термической подготовки фосфорного сырья: обжиг кускового фосфорита, окатышей и агломерирование фосфоритовой мелочи.
Эффективность использования энергии в технологических процессах определяется возможностью управления физико-химическими превращениями, протекающими в фосфатном сырье при термической подготовке и переработке на базе интенсификации тепло- и массообмена. В свою очередь управление и оптимизация химико-технологических и тепло- и массообменных процессов зависит от степени их изученности, глубины понимания всей картины явлений в рассматриваемой технологии.
Основание для более углубленного изучения процессов – низкая на сегодняшний день эффективность использования материальных и энергетических ресурсов в процессах и аппаратах фосфорной промышленности. Так, по результатам длительной эксплуатации, коэффициент использования мощности руднотермических печей составляет:
|
KM |
Тип руднотермической печи |
|
0,69 |
РКЗ-48Ф |
|
0,53 |
РКЗ-72Ф |
|
0,47 |
РКЗ-80Ф |
Невысоким является и коэффициент использования календарного времени KM ≈ 0,85. Ухудшает положение и тот факт, что при снижении мощности относительно номинальной резко возрастает удельный расход электроэнергии от 14,5 до 20 МВт×ч/т. Кроме того, изменение режима часто приводит к снижению качества и получению содержания P2O5 в шлаке.
Для схемы термической подготовки фосфоритовой мелочи путём агломерации характерен низкий процент годного агломерата и невысокая степень использования вторичных энергоресурсов аглопроцессе.
При обжиге фосфоритовых окатышей наблюдается повышенное количество возврата и низкая устойчивость окатышей к истиранию. С учётом тенденций к обеднению руд проблема создания высокоэффективных ресурсоэнергосберегающих технологических процессов для повышения производительности оборудования или хотя бы поддержания их на существующем уровне становится весьма актуальной на современном этапе.
Поиск оптимальных условий протекания процессов на действующем оборудовании – задача весьма сложная, дорогостоящая из-за множества факторов, влияющих на конечный результат. Именно поэтому предпочтение отдаётся лабораторным экспериментальным установкам, а также математическому моделированию процессов и аппаратов, технологических схем в целом и отысканию на базе разработанных математических моделей оптимальных режимов работы оборудования и способов воздействия на процессы с целью повышения их эффективности. Из стохастических и детерминированных моделей наиболее предпочтительными считаются последние, позволяющие более обоснованно учитывать всю совокупность параметров, влияющих на ход процесса, их взаимосвязь с выходом продукта. Однако такой подход требует подробного изучения закономерностей физико-химических превращений и тепло- и массообменных характеристик сырьевых материалов, продукта и промежуточных компонентов, участвующих во всех стадиях технологического процесса.
По термическому способу получения фосфора проведены обширные исследования. Накоплен богатый экспериментальный материал по физико-химическим процессам в расплаве, изучены технологические особенности аглопроцесса, обжига кускового и окатанного фосфорита, получены количественные и качественные закономерности по большинству параметров, определяющих выход конечного продукта. Несмотря на то, что все эти процессы высокотемператрурные, сопровождающиеся большими затратами тепловой и электрической энергии, вопросам тепломассопереноса в технологии производства фосфора посвящено совсем немного исследований.
Предлагаемая работа ставит задачу восполнить сведения, необходимые для описания тепло- и массообменных процессов в теплотехнологических аппаратах фосфорного производства на базе детерминированных математических моделей. Рассматриваемые математические модели тепловых и газодинамических процессов используются для оптимизации режимов работы технологического оборудования, а также расчётов параметров технологических агрегатов при проектировании.
Эффективность использования энергии в технологических процессах определяется возможностью управления физико-химическими превращениями, протекающими в сырьевом материале при термической подготовке и переработке на базе интенсификации тепло- и массообмена. В свою очередь управление и оптимизация физико-химических и тепло- и массообменных процессов зависит от степени их изученности, глубины понимания всей картины явлений в рассматриваемой технологии [7].
Управление, например, процессом обжига сырьевых материалов с целью установления и поддержания рациональных тепловых режимов работы конвейерной обжиговой машины приводит к необходимости изучения стационарного и динамического режимов работы плотного слоя [3]. Для этого необходимо иметь представление о внутреннем тепловом состоянии материала, влияющем на физико-химические превращения и общую картину в слое [2].
В данной работе рассматривается задача оптимального управления внутренним тепловым состоянием системы с распределенными (во времени и пространстве) параметрами, произвольной геометрии (шар, цилиндр, плоскость). Управляющими параметрами являются коэффициенты системы ρс и λ. В качестве критерия оптимальности принято наименьшее отклонение от заданного распределения температуры T*(τ, x) [1, 14], которая заключается в отыскании теплофизических характеристик материалов.
Вообще говоря, обратные задачи являются некорректно поставленными по Адамару [14], поэтому необходимо применение «регуляризующих» алгоритмов. В данной работе использован принцип «естественной регуляризации», основанный на «вязкостных» свойствах вычислительных алгоритмов [1].
Математическая модель теплопереноса
Перенос тепла в окомкованном материале (окатыше) осуществляется теплопроводностью при наличии химических неизотермических реакций, описываемых феноменологически [2]. Математическая модель представлена уравнениями:
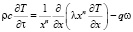; (1)
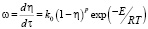(2)
начальные и граничные условия:
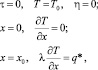(3)
где λ – коэффициент теплопроводности материала; τ и x – соответственно временная и пространственная координаты; ρ – плотность материала; c – удельная изобарная теплоемкость; η – степень реагирования; k0 – коэффициент проницаемости; Е – энергия активации; q – тепловой эффект реакции; n – показатель, характеризующий геометрию системы (0 – плоскость, 1 – цилиндр, 2 – шар); q* – тепловой поток на границе.
Распределение температуры T*(τ, x) получено в численном эксперименте решением прямой задачи, где ρс и λ являются функциями температуры.
При решении нелинейных задач аналитическими методами возникают существенные математические трудности, которые требуют разработки специальных методов решения [1]. Причем возможность получения аналитического решения и выбор метода существенным образом зависят от вида нелинейностей в дифференциальных уравнениях и в граничных условиях. Численное решение рассматриваемой нелинейной задачи представляется единственно возможным.
Уравнения (1) и (2) и граничные условия (3) записываются в неявной разностной форме. При этом учтено, что ρс, λ, η зависят от температуры а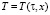 
.
Разностные уравнения имеют вид:
;
; 
.
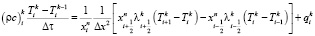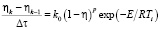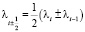а) 
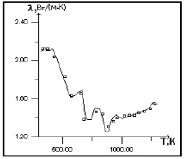б)
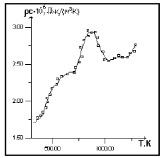
График зависимости от температуры, полученный в результате решения задачи, коэффициента объемной теплоемкости (а) и коэффициента теплопроводности (б);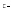 
экспериментальные данные
Решение прямой задачи методом прогонки дает возможность получить T*(τk, xi).
Численный эксперимент определения теплофизических характеристик материала
Задача оптимального управления ставит целью определить ρс и λ так, чтобы T(τk, xi) – решение задачи (1–3) как можно меньше отличалось от T*(τk, xi), то есть чтобы функционал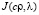 
был минимальным.
.
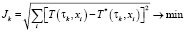Следуя Алифанову [1] функционал Jk на каждом временном слое будем называть невязкой. Последовательно на каждом временном слое ρс и λ определяются из условия минимума невязки.
Рассмотрим метод деформируемого многогранника [13], несколько более сложный по сравнению с прямым поиском, но оказавшийся весьма эффективным и легко осуществляемым на ЭВМ. Он исключает определенные практические трудности при использовании регулярных симплексов, а именно отсутствие ускорения поиска и трудности при проведении поиска на искривленных поверхностях – «оврагах» и «хребтах».
При практической реализации на ЭВМ многих методов нелинейного программирования значительная доля машинного времени тратится на то, чтобы обеспечить строгое выполнение требований допустимости.
Алгоритм скользящего допуска [12] позволяет улучшить значения целевой функции как за счет информации, получаемой в допустимых точках пространства решений, так и за счет информации, которую удается получить при прохождении через некоторые точки, лежащие вне допустимой области, но являющиеся близкими к допустимым.
Алгоритм скользящего допуска с оптимизацией по методу деформируемого многогранника реализован при решении данной задачи [10].
Причем, в силу реализуемости конкретного физико-технического процесса, на ρс и λ были наложены следующие ограничения: 0 < λ < 5, 0 < ρс < 5E + 10.
Для увеличения скорости нахождения минимума невязки на каждом последующем временном слое (шаге), в качестве начальной точки поиска, берется найденная точка минимума на предыдущем временном слое (шаге).
Решение задачи реализовано в виде программы на языке Borland C++.
Результаты решения задачи для окатанного фосфорита совпадают с экспериментальными данными [11] и представлены на рисунке.
Заключение
Предложенный алгоритм и разработанная программа могут быть использованы для широкого круга задач подобного типа без существенных изменений [8]. По результатам расчетов видно, что управление посредством коэффициентов ρс, λ дает возможность осуществить программируемый нагрев с высокой точностью и, следовательно, удовлетворить необходимым технологическим условиям [5].
На практике обжиг окатышей проводится в обжиговых машинах конвейерного типа [6]. Рассматривая обжиг в плотном слое, можно получить полную картину протекания физико-химических процессов [9].
Оптимальное управление целевыми процессами в слое с учетом полученных данных и на основе представленной математической модели позволит максимально снизить количество возврата и обеспечить ресурсо- и энергосберегающие условия функционирования обжиговых агрегатов [4].