К числу явлений, неблагоприятно сказывающихся на функциональных характеристиках заготовки для световодного волокна, получаемой методом MCVD [3, 5], относится возникновение сублимации частиц, уже осевших на боковую поверхность опорной трубки, при проплавлении слоя. Для описания этого явления разумно использовать методику, предложенную в работе [4] и эффективно апробированную при исследовании сублимации стенок плоского канала. Описание течения в круглой трубке при более реалистичном пуазейлевском профиле скорости значительно усложняет задачу, поэтому последовательное претворение идей авторов работы [1, 2, 4] оказывается весьма затруднительным. Попытаемся получить приближенное решение, используя вариационную методику.
В рамках геометрии задачи, представленной на рис. 1, проанализируем течение газа-носителя со взвешенными в нем частицами, принимая во внимание сублимацию напыленного слоя.
Предполагается, что изменение радиуса трубки в результате сублимации происходит настолько медленно, что не влияет на характер процессов переноса. Поток газа считается гидродинамически стабилизированным с пуазейлевским профилем скорости и равномерным распределением температуры T0 в начальном сечении. Кроме того, входящий поток несет в себе напыляемые частицы концентрации C0, меньшей, чем концентрация насыщения, соответствующая температуре T0 и полному давлению.
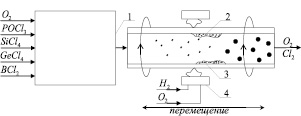
Рис. 1. Схема модифицированного метода химического парофазного осаждения (MCVD): 1 – измерители и регуляторы расхода компонентов; 2 – трубка из плавленого кварца; 3 – осажденный слой; 4 – многосопловая горелка
Исходным пунктом анализа будут уравнения, выражающие законы сохранения энергии и массы в безразмерной форме
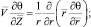 (1)
(1)
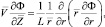 (2)
(2)
где использованы безразмерные переменные:
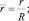
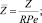
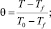
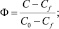
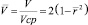 (3)
(3)
(величины с индексом f относятся к полностью развитому состоянию; 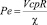 – число Пекле;
– число Пекле; 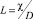 – число Льюиса).
– число Льюиса).
При записи уравнений (1)–(2) сделаны предположения о малости поперечной составляющей скорости при изменении координаты Z. Кроме того, считаются неизменными физические характеристики процессов, а также предполагается, что скрытая теплота сублимации подводится в основном несущим газом, так что теплообменом «сублимирующаяся поверхность – внешняя среда» можно пренебречь. В результате выявляется прямая зависимость концентрации паров сублимирующегося материала от величины подводимого тепла, т.е. от поля температур. Эта зависимость и порождает основные сложности в решении системы уравнений (1)–(2) [4].
Достаточно тонкий анализ баланса потоков массы и тепла [4] на боковой поверхности трубки даёт краевое условие
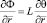 при
при 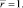 (4)
(4)
Второе краевое условие можно установить из требования равенства на стенке концентрации сублимирующегося материала концентрации насыщенных паров для системы «твердое тело – пар». В рамках построенной в работе [4] линейной модели состояния насыщения –
C = aT + b. (5)
Это условие имеет вид
Ф = –ks θ при 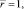 (6)
(6)
где 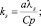 λs, Cp – скрытая теплота сублимации и удельная теплоемкость при постоянном давлении соответственно, а постоянная a определяется соотношением (5) и находится из формулы [2]
λs, Cp – скрытая теплота сублимации и удельная теплоемкость при постоянном давлении соответственно, а постоянная a определяется соотношением (5) и находится из формулы [2]
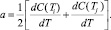
Здесь Ti и Tj – задают диапазон температур, для которых строится аппроксимация. Завершается постановка задачи введением условий цилиндрической симметрии
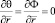 (7)
(7)
и условий в начальном сечении
θ = Ф = 1 при 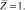 (8)
(8)
Решение системы уравнений (1)–(2) с краевыми условиями (4)–(8) будем искать вариационным методом, основанным на общей схеме построения термодинамических лагранжианов [5]. Используя общие принципы, сразу можем записать вариационную переформулировку рассматриваемой краевой задачи:
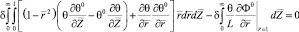 (9)
(9)
для процесса теплопроводности и
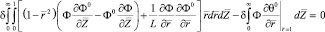 (10)
(10)
для процесса массопереноса.
Будем искать решение в виде
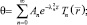 (11)
(11)
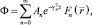 (12)
(12)
где λn, γn – собственные значения, а Tn, Fn – собственные функции, вид которых неизвестен.
Сопоставляя разложения (11) и (12) с краевыми условиями (4) и (6), приходим к выводу, что λn = γn.
Подставляя выражения для температуры и концентрации (11)–(12) и интегрируя по 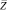 , получаем для каждого λn и каждой функции Tn и Fn условия
, получаем для каждого λn и каждой функции Tn и Fn условия
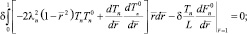 (9а)
(9а)
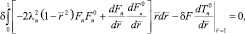 (10а)
(10а)
позволяющие в принципе решить поставленную задачу на основе аппроксимационной схемы Ритца. Для этого представим собственные функции Tn и Fn в виде разложения Неймана по функциям Бесселя:
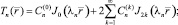 (13)
(13)
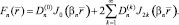 (14)
(14)
Рассмотрим одночленную аппроксимацию. В этом случае краевые условия приводят к системе уравнений, связывающих λn и βn:
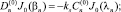 (4а)
(4а)
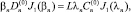 (5а)
(5а)
откуда
 (15)
(15)
Кроме того, подставляя представления для Tn и Fn в формулировки (9а) и (10а) и производя варьирование по 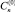 и
и 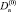 (
(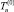 и
и 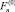 считаются постоянными на время варьирования), получаем систему уравнений
считаются постоянными на время варьирования), получаем систему уравнений
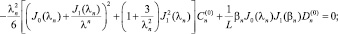 (16)
(16)
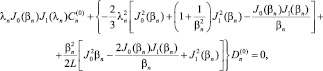 (17)
(17)
линейную относительно коэффициентов 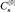 и
и 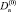 . Нетривиальные решения существуют, если равен нулю определитель, составленный из коэффициентов, стоящих при
. Нетривиальные решения существуют, если равен нулю определитель, составленный из коэффициентов, стоящих при 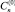 и
и 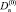 . Это условие дает второе уравнение, которое вместе с уравнением (15) позволяет найти λn и βn. В таблице приведены собственные значения λn и βn для некоторых наборов параметров L и ks, рассчитанные методом Стеффенсона.
. Это условие дает второе уравнение, которое вместе с уравнением (15) позволяет найти λn и βn. В таблице приведены собственные значения λn и βn для некоторых наборов параметров L и ks, рассчитанные методом Стеффенсона.
Для того чтобы получить решение в окончательном виде, необходимо разработать методику вычисления коэффициентов 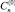 и
и 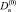 и Ak.
и Ak.  можно определить из условия нормировки собственных функций Fk, из которого непосредственно следует представление
можно определить из условия нормировки собственных функций Fk, из которого непосредственно следует представление
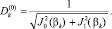 (18)
(18)
Коэффициенты 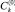 найдем из краевого условия (4а).
найдем из краевого условия (4а).
Собственные значения λn и βn для различных комбинаций определяющих параметров процесса сублимации*
|
L |
ks |
λn |
βn |
L |
ks |
λn |
βn |
|
3,0 |
1,0 |
1,397 |
2,990 |
3,0 |
1,0 |
1,161 |
2,504 |
|
2,521 |
5,434 |
2,653 |
5,502 |
||||
|
3,566 |
7,414 |
3,760 |
7,855 |
||||
|
4,627 |
9,268 |
5,571 |
8,651 |
||||
|
6,744 |
13,725 |
5,832 |
11,79 |
||||
|
7,801 |
15,537 |
6,941 |
14,179 |
||||
|
0,81 |
0,1 |
2,154 |
2,433 |
0,81 |
1,0 |
2,262 |
2,593 |
|
5,244 |
5,556 |
2,979 |
4,510 |
||||
|
8,307 |
8,699 |
3,721 |
3,920 |
||||
|
14,416 |
15,002 |
5,326 |
5,767 |
||||
|
0,81 |
10,0 |
2,390 |
2,592 |
8,434 |
8,930 |
||
|
3,691 |
3,843 |
9,881 |
10,407 |
||||
|
5,496 |
5,813 |
11,544 |
12,200 |
||||
|
8,830 |
10,541 |
12,944 |
13,629 |
||||
|
0,81 |
1,0 |
14,653 |
15,276 |
||||
|
16,007 |
16,847 |
Примечание. *В таблице указаны не все собственные значения, которых, по-видимому, бесконечное множество, а только лежащие в пределах от 0 до 16,0.
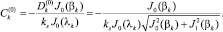 (19)
(19)
Из условия однородности температуры и концентрации во входном сечении для нахождения коэффициентов An получаем формулу
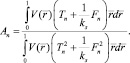 (20)
(20)
Зависимость приближенных профилей температуры и концентрации от параметров L и ks приведена на рис. 2–4.
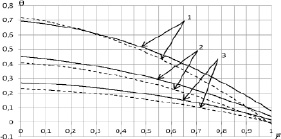
Рис. 2. Зависимость профиля температуры от параметра ks (L = 0,81): 1 – 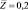 ; 2 –
; 2 – 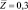 ; 3 –
; 3 – 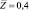 ; ks = 0,1 – сплошная линия; ks = 1,0 – пунктирная линия
; ks = 0,1 – сплошная линия; ks = 1,0 – пунктирная линия
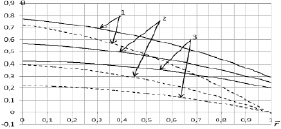
Рис. 3. Зависимость профиля температуры от числа Льюиса (ks = 1,0): 1 – 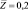 ; 2 –
; 2 – 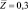 ; 3 –
; 3 – 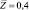 ; L = 3,0 – сплошная линия; L = 0,81 – пунктирная линия
; L = 3,0 – сплошная линия; L = 0,81 – пунктирная линия
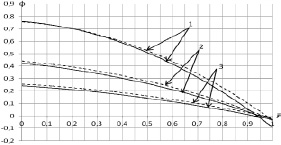
Рис. 4. Сравнение профилей концентрации для различных значений числа Льюиса (ks = 0,1): L = 3,0 – сплошная линия; L = 0,81 – пунктирная линия; 1 – 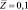 ; 2 –
; 2 – 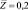 ; 3 –
; 3 – 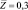
В случае L = 0,81 профили температуры слабо зависят от изменения коэффициента ks при ks ≤ 1,0. Эта зависимость усиливается с увеличением ks и становится весьма значительной при ks > 10,0 Указанный результат допускает следующее объяснение: малые значения числа Льюиса соответствуют сравнительно малым значениям теплопроводности, так что при слабом взаимодействии на стенке процессов тепло- и массопереноса (ks ≤ 1,0, следовательно, мало значение коэффициента a) это взаимодействие на областях, близких к оси трубки, сказывается постепенно, увеличивая отличие профилей температуры, соответствующих различным ks вниз по течению (рис. 3). Процесс для ks = 10,0 протекает при сильном взаимодействии полей температуры и концентрации, что вызывает существенное изменение профиля температуры даже при малых коэффициентах температуропроводности. При L = 3,0 профили температуры более пологие, и достижение полностью развитого состояния происходит при больших 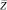 , причем крутизна профилей увеличивается с увеличением коэффициента ks как для L ≤ 1,0, так и для L > 1,0. Приведенный результат находится в согласии с общими представлениями о теплообмене, так как увеличение числа Льюиса означает уменьшение потока массы на стенке (рис. 5), что в свою очередь уменьшает тепловой поток (формула (4)) и приводит к более медленному изменению профиля температуры. Эффектом, аналогичным слабой зависимости профиля температуры от ks при L ≤ 1,0, является сравнительно слабая зависимость от ks профиля концентрации при L > 1,0. Для его объяснения можно привлечь подобные соображения. Анализ результатов позволяет сделать вывод о том, что профили концентрации, в противоположность профилям температуры, в значительно большей степени чувствительны к изменению потока массы. Существенные отклонения наблюдаются лишь для значений ks > 1,0 и на начальном участке течения.
, причем крутизна профилей увеличивается с увеличением коэффициента ks как для L ≤ 1,0, так и для L > 1,0. Приведенный результат находится в согласии с общими представлениями о теплообмене, так как увеличение числа Льюиса означает уменьшение потока массы на стенке (рис. 5), что в свою очередь уменьшает тепловой поток (формула (4)) и приводит к более медленному изменению профиля температуры. Эффектом, аналогичным слабой зависимости профиля температуры от ks при L ≤ 1,0, является сравнительно слабая зависимость от ks профиля концентрации при L > 1,0. Для его объяснения можно привлечь подобные соображения. Анализ результатов позволяет сделать вывод о том, что профили концентрации, в противоположность профилям температуры, в значительно большей степени чувствительны к изменению потока массы. Существенные отклонения наблюдаются лишь для значений ks > 1,0 и на начальном участке течения.
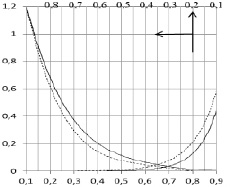
Рис. 5. Влияние параметра ks на поток массы у боковой поверхности трубки при различных числах Льюиса: ks = 0,1 – сплошная линия; ks = 1,0 – пунктирная линия
Наибольший практический интерес представляет исследование сублимационного потока на боковой поверхности (рис. 5). Из представленных зависимостей следует однозначный вывод о том, что уменьшения сублимационного слоя можно добиться, осуществляя процесс напыления на максимально возможных числах Льюиса и значениях параметра ks.



