Достижения в области технологии формирования полупроводниковых структур и разработка новых технологий наноэлектроники нуждаются в более точных измерениях параметров диффузионного процесса и хороших теоретических моделях для его описания. В настоящее время экспериментальные и теоретические исследования диффузионных процессов в наноразмерных поверхностных слоях находятся на стадии развития [3, 7]. Изучение процессов диффузии ведется в направлении создания на основе экспериментальных результатов более точных моделей, которые давали бы возможность предсказывать протекание процесса диффузии путем теоретического анализа. Современные спектрометрические методы позволяют обеспечить необходимую точность измерений профилей распределения примесей в таких слоях.
Используя полученные значения распределения сегрегировавших элементов в поверхностный слой кристалла и кинетические кривые, можно определить коэффициенты диффузии компонентов в поверхностном слое. Это позволяет провести анализ диффузионных процессов, происходящих в поверхностном слое кристалла, в различных классах материалов при сегрегации. В [4] для определения коэффициента диффузии использовали профиль распределения элементов в поверхностном слое, полученном методом рентгено-электронной спектроскопии в сочетании с ионным распылением. Простейшая модель предполагает, что в результате сегрегации и ионной бомбардировки образуется измененный слой толщиной с постоянной (усредненной) концентрацией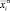 
в этом слое, отличный от объемного состава. В рамках этой модели определяется концентрационная зависимость поверхностного слоя 
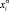от времени травления t и , и исходя из этого определяют коэффициент диффузии в поверхностном слое в виде
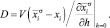(1)
В работе [5] определены параметры диффузии кремния в тонких эпитаксиальных пленках германия по концентрационным профилям, полученным методом вторично-ионная масс-спектрометрия. Определение коэффициента диффузии кремния в германии проводилось путем сравнения экспериментальных кривых выхода ионов Si по глубине пленки (h) с рассчитанными по формуле
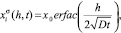(2)
где D – искомый коэффициент; t – время отжига.
Кроме того, на практике широко используется модель Кранка, в которой для полубесконечного кристалла поверхностная концентрация определяется соотношением
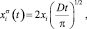(3)
где xi – объемная концентрация. Анa- логичные уравнения были получены и в работах [8, 9] и установили, что процесс сегрегации на поверхности кристалла лимитируется диффузией и подчиняется закону t1/2, а температурная зависимость – закону Аррениуса.
В [1] получено такое же соотношение для концентрационного профиля распределения элементов в поверхностном слое, путем аппроксимации полученных экспериментальных кривых в видe
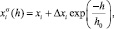(4)
где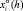 
и xi – концентрации компонента i на глубине h и в объеме кристалла соответственно, 
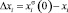; h0 – глубина при которой концентрация меняется в е раз и рассчитывается с использованием экспериментальных данных по формуле
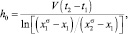(5)
где 
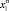и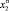 
– значения концентраций первого и второго компонентов сплава, полученные – на вторично-ионном масс-спектрометре в момент времени t1 и t2; V – скорость распыления, определяемая из соотношения 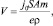[6]
(6)
где j0 – плотность тока первичных ионов на мишени, А•см–2; m = 1 а.е.м; е – заряд электрона; – плотность мишени; А – относительная атомная масса мишени.
В настоящей работе с использованием данных по исследованию поверхностной сегрегации легирующих примесей на атомарно чистых поверхностях (111) монокристаллов кремния, легированных фосфором и сурьмой (КЭФ-0.3 и КЭС-0.01), получены аналогичные результаты и характер изменения концентрации аппроксимируется соотношением (4). Исследуемые образцы вырезались корундовой иглой из пластин кремния, прошедших стандартную механическую обработку и помещались в рабочую камеру спектрометра. Очистку поверхности проводили циклами ионно-аргонной бомбардировки с последующим высокотемпературным отжигом. О чистоте поверхности судили по оже спектрам. На рис. 1 представлены исходная и очищенная поверхности монокристалла КЭФ-0.3, полученные методом атомно-силовой микроскопии (АСМ) в полуконтактном (прерывисто-контактном) режиме с использованием резонансных колебаний кантилевера на сканирующем зондовом микроскопе Solver PRO производства ЗАО «НТ-МДТ» (г. Зеленоград).
Из экспериментальных результатов можно получить общую закономерность кинетики поверхностной сегрегации в виде
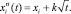(7)
Опираясь на второе уравнение Фика и принимая, что коэффициент диффузии D не зависит от концентрации,
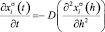(8)
и пользуясь уравнениями (4) и (6), при определенных условиях эксперимента можно получить наиболее точные значения коэффициента диффузии в поверхностном слое. Для этого левую часть (8) преобразуем в виде
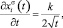(9)
а правую часть, дифференцируя (4)
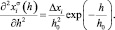(10)
а б
Рис. 1. 3 D изображение исходной поверхности кремния, легированного фосфором КЭФ-0.3 (111) (а) и после ионно-аргонного травления (б)
Тогда коэффициент диффузии в поверхностном слое на глубине h можно рассчитать по формуле
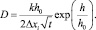(11)
Формула для расчета коэффициента диффузии на поверхности кристалла (при h = 0) примет вид
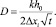(12)
В расчетах следует принимать за t время, в течение которого на поверхности кристалла происходит перераспределение концентрации элементов. Поэтому в экспериментах следует определять время, за которое проведен отжиг, причем нет необходимости проводить отжиг до насыщения поверхности при данной температуре. Важно чтобы были определены профиль распределения и изменение концентрации элементов на поверхности по сравнению с объемом за это время t. Расчет коэффициента D при данной температуре проводился нами по этой схеме с использованием экспериментальных данных по временной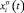 
и глубинной 
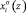зависимости состава поверхности, полученных методами оже-электронной спектроскопии и вторично-ионной масс-спектрометрии (рис. 2–3).
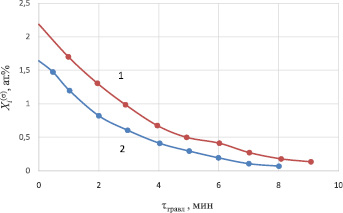
Рис. 2. Профили распределения фосфора (1) и сурьмы (2) в образцах КЭФ-0.3 (111) и КЭС-0.01 (111), полученные методом электронной оже-спектроскопии. Температура отжига 423 К(1), 498 К(2) [2]
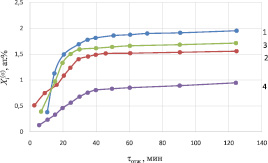
Рис. 3. Кинетика поверхностной сегрегации фосфора (1, 3) и сурьмы (2, 4) на гранях (111) образцов КЭФ-0.3 и КЭС-0.01. Температура отжига 418 (1), 468 (2), 498 (3) и 403 К (4) [2]
Коэффициенты диффузии фосфора и сурьмы в кремнии при различных температурах
|
P |
Sb |
||
|
Т, К |
D, см2/с |
Т, К |
D, см2/с |
|
423 |
7,13•10–17 |
503 |
2,56•10–17 |
|
433 |
1,55•10–16 |
513 |
5,13•10–17 |
|
443 |
3,26•10–16 |
523 |
1,00•10–16 |
|
453 |
6,62•10–16 |
533 |
1,91•10–16 |
|
463 |
1,30•10–15 |
543 |
3,54•10–16 |
|
473 |
2,50•10–15 |
553 |
6,43•10–16 |
|
483 |
4,65•10–15 |
563 |
1,14•10–15 |
|
493 |
8,46•10–15 |
573 |
1,99•10–15 |
|
503 |
1,50•10–14 |
583 |
3,41•10–15 |
|
513 |
2,61•10–14 |
593 |
5,73•10–15 |
|
523 |
4,43•10–14 |
603 |
9,47•10–15 |
|
533 |
7,38•10–14 |
613 |
1,54•10–14 |
|
543 |
1,21•10–13 |
623 |
2,46•10–14 |
|
553 |
1,94•10–13 |
633 |
3,88•10–14 |
|
563 |
3,06•10–13 |
643 |
6,02•10–14 |
|
573 |
4,75•10–13 |
653 |
9,23•10–14 |
|
583 |
7,28•10–13 |
663 |
1,40•10–13 |
|
593 |
1,10•10–12 |
673 |
2,09•10–13 |
|
603 |
1,64•10–12 |
||
Значение коэффициента k в формуле (12) определялось из зависимости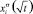 
. Так как концентрация примеси в объеме очень мала, принималось 
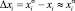, a h0 определяли по уравнению (5) с использованием данных из распределения элементов по глубине. Из экспериментальных результатов так же оценивали энергию активации диффузии Еа из соотношения 
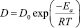и с ее помощью рассчитывались значения коэффициента диффузии при других температурах. Значение энергии активации диффузии Ea составляло 118 и 149 кДж/моль, а предэкспоненциального множителя D0 – 2,88•10–4 и 8,5•10–4 м2/с для фосфора и сурьмы соответственно. Рассчитанные нами значения коэффициентов диффузии фосфора и сурьмы при различных температурах отжига представлены в таблице.
Таким образом, используя экспериментальные результаты по распределению элементов в поверхностном слое, рассчитан коэффициент диффузии D в интервале температур 423–603 К для примесей фосфора и сурьмы в кремнии и получены значения энергии активации диффузии Ea и предэкспоненциального множителя D0 в уравнении диффузии для легирующих элементов.