Развитие многих современных технологий тесно связано с решением задачи управления процессами смачивания и растекания жидких фаз по поверхности твердых тел в различных внешних полях [2–8].
Один из способов оказания влияния на динамику процесса растекания капли вязкой жидкости может быть основан, например, на использовании известного термокапиллярного эффекта Марангони.
Одной из основных проблем при исследовании процесса неизотермического растекания капли по твердой поверхности остается перемещение линии трехфазного контакта, которое приводит в уравнениях Навье – Стокса к недопустимой сингулярности силы при граничных условиях прилипания [8].
Если для макроскопических масштабов такое приближение (условие прилипания) вполне удовлетворительно, то для микроскопических масштабов из-за возможного скольжения жидкости по твердой поверхности такое приближение должно быть пересмотрено.
Рассмотрим в декартовой системе координат процесс симметричного, относительно вертикальной оси Oz, растекания вязкой ньютоновской двумерной капли по обе стороны оси Ox, совпадающей с горизонтальной гладкой поверхностью твердого тела.
Предположим, что температура подложки неоднородна, то есть температура в центре капли (x = 0) и на ее периферии x = x0(t) в любой момент времени t принимает значения T1T2 соответственно, причем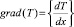 
является постоянной и положительной величиной.
При небольшой высоте капли распространение температуры в жидкости происходит значительно быстрее распространения самой жидкости по твердой поверхности. Поэтому можно считать, что температура остается постоянной от основания до свободной поверхности капли. Следовательно, проекция вектора grad(T) на свободной поверхности z = f(x, t) на ось Ox совпадает со значением температуры подложки в точке с соответствующей абсциссой.
Для описания движения двумерной капли в рассматриваемой системе воспользуемся уравнениями Навье – Стокса в приближении «теории смазки» [3]. В данном случае эти уравнения имеют вид
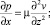
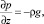(1)
где p – давление в жидкой фазе; v – горизонтальная компонента скорости капли; – динамическая вязкость; – плотность жидкости; g – ускорение силы тяжести.
Так как поверхностное натяжение жидкости на границе раздела с газообразной средой существенно зависит от температуры, то наличие grad(T) приводит к возникновению grad(). Течение жидкости под действием напряжения сдвига, обусловленного наличием на ее поверхности градиента температуры, известно под названием эффекта Марангони.
Условие отсутствия касательного напряжения на границе раздела жидкости и газообразной среды имеет вид
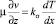при z = f(x, t), (2)
где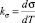 
– температурный коэффициент поверхностного натяжения жидкости.
Заметим, что поверхностное натяжение жидкости , как правило, уменьшается с ростом температуры, то есть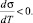 
Будем полагать далее, что поверхностное натяжение жидкости (T) линейно зависит от температуры и k = const < 0.
С учетом специфики задачи, на границе раздела жидкости с твердым телом примем вместо обычного условия прилипания, как в [3], условие
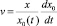при z = 0. (3)
Условие (3) сочетает в себе прилипание капли вязкой жидкости в центре (x = 0) к подложке с перемещением ее точки трехфазного контакта x = x0(t) со скоростью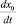 
.
Условие равенства нулю высоты свободной поверхности капли в точке трехфазного контакта запишем в виде
f(x, t) = 0 при x = x0(t). (4)
С учетом граничных условий (2) и (3) проинтегрируем дважды первое уравнение (1) и получим
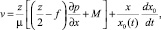(5)
где M = –k grad(T) > 0.
Уравнение неразрывности в рассматриваемом двумерном случае имеет вид
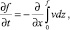(6)
а давление в капле без учета действия капиллярных эффектов равно
p = p0 – g(z – f), (7)
где p0 – давление в газовой среде над свободной поверхностью капли.
Подстановка выражения для скорости (5), записанная с учетом (7), дает уравнение гравитационно-термокапиллярного растекания двумерной капли вязкой жидкости по неравномерно нагретой подложке с учетом условия скольжения
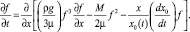(8)
Условие сохранения площади сечения валика S0 (объема капли) в любой момент времени, с учетом ее симметрии, запишется для двумерного случая в виде нелокального интегрального условия
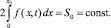(9)
В нормализованных переменных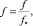 
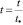уравнение (8) и условие (9) запишем в безразмерной форме
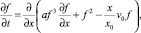(10)
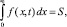(11)
где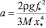 
– безразмерный параметр;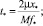 
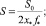v0 – безразмерная скорость растекания; f*, x*, t* – характерные значения высоты, горизонтального размера капли и времени соответственно.
Заметим, что аналитического решения модельной задачи неизотермического растекания на основе нелинейного уравнения (10) с неклассическим интегральным условием (11) не существует, а численное ее решение представляет большие трудности.
Для исследования модельной задачи применим квазистационарный подход [1, 3].
Выполним в (10) переход к новым переменным
= x – x0(t);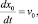 
(12)
временно «замораживая» скорость распространения капли v0, и получим
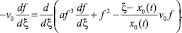(13)
Поскольку в данной постановке не следует ожидать разрыва профиля свободной поверхности капли на периферии, то примем условие
f = 0 при = 0, (x = x0(t)). (14)
Интегрирование (13) с условием (14) дает соотношение
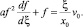(15)
Для удобства дальнейшего исследования, следуя [4] , путем замены
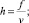
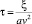(16)
приведем задачу Коши (15), (14) к инвариантной форме
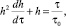0 < 0. (17)
h = 0 при = 0. (18)
Нелокальное условие (11) в новых переменных примет вид:
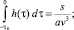
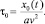(19)
С учетом (18) и (19) проведем интегрирование (17) и получим соотношение
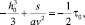(20)
где h0 = h(–0) – нормализованная высота капли в центре ( = –0; = –x0(t), x = 0).
В центре капли справедливо условие прилипания и интегрирование уравнения
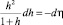
дает при значениях переменных = –0; = –x0(t), т.е. x = 0 зависимость
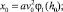
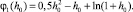(21)
Если учесть, что, с учетом (20), из (21) следует
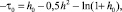(22)
то из (20), принимая во внимание (22), получим зависимость
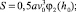
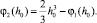(23)
Из системы (21) и (23) найдем далее выражения для абсциссы точки трехфазного контакта
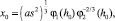(24)
безразмерной скорости растекания
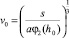(25)
и скорости изменения нормализованной высоты капли со временем
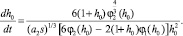(26)
Дополним уравнение (26) начальным условием
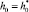при t = 0. (27)
Таким образом, квазистационарная модель задачи гравитационно-термокапиллярного растекания свелась к системе алгебро-дифференциальных уравнений (17), (18), (24)(27). На основе данной системы, с учетом (16), можно рассчитать положение точки трехфазного контакта x0, скорость перемещения периферийной части капли v0 и профиль свободной поверхности капли h = h(x, t) в любой момент времени t. Для численной реализации задач Коши (17), (18) и (26), (27) можно применить, например, метод Рунге Кутты четвёртого порядка точности.
Пользуясь приближенными методами анализа, из (21) и (22) получим закономерности перемещения точки трехфазного контакта на начальной (h0 << 1) стадии растекания
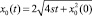(28)
и конечной (h0 >> 1) стадии растекания
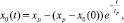(29)
где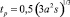 
– безразмерное время перехода капли к равновесному состоянию. Заметим, что задача чисто термокапиллярного растекания (a/M << 1) при x0 (0) = 0 c условием прилипания допускает автомодельное решение вида
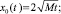M > 0, (30)
которое, в отличие от квазистационарного решения с условием прилипания, точно совпадает с решением задачи растекания капли в нагретую сторону (grad(T) > 0) с условием проскальзывания.
Полученные результаты подтверждают, что при растекании капли в нагретую сторону термокапиллярный эффект препятствует процессу растекания, так как поверхностное натяжение у края капли в рассматриваемом случае меньше, чем у ее центральной части.
Анализ результатов моделирования показывает, что квазистационарный подход и использование условия скольжения при исследовании задачи растекания капли вязкой жидкости по твердой поверхности дает качественное и количественное согласие c моделируемым физическим процессом и такое моделирование может быть использовано при разработке и численном исследовании математических моделей более высокого иерархического уровня.