Промышленное оборудование непрерывного применения составляет значительную долю современного технологического парка средств производства в различных отраслях экономики. В наибольшей степени к данному виду техники относится оборудование газо- и нефтеперерабатывающих и добывающих комплексов, автоматических и автоматизированных машиностроительных производств конвейерного типа, систем мониторинга параметров объектов управления в космической технике, энергетике, медицине, атомной, химической промышленности и в военном деле. Особенностью такого оборудования является необходимость обеспечения непрерывного и качественного функционирования в течение заданных длительных интервалов эксплуатации [3]. Перерывы в функционировании при этом жестко регламентированы планами целевого применения и используются в основном для поддержания оборудования в удовлетворительном техническом состоянии, а также для восполнения расходуемых в процессе функционирования запасов материальных ресурсов.
Перерывы в применении по назначению отрицательно влияют на суммарный объем выпуска продукции, однако вообще без них обойтись невозможно, так как в этом случае снижается качество выпускаемой продукции из-за изменения в процессе эксплуатации значений параметров технического состояния элементов оборудования вследствие действия процессов старения, износа и разрегулирования. При достижении параметрами технического состояния заданных предельно допустимых значений (границ контрольных допусков) возникает потребность в регулировании параметров. В этих условиях важное значение приобретает задача повышения точности определения граничных значений полей контрольных допусков параметров технического состояния [2, 4].
В статье рассматриваются вопросы моделирования влияния погрешности задания граничных значений полей контрольных допусков на качество функционирования промышленного оборудования непрерывного использования. Кроме того, предложен способ определения границ области допустимых значений погрешности задания контрольных допусков, основанный на введении максимально допустимой величины обобщенного ущерба от неточности задания допусков.
Формулировка проблемы и противоречий
Существующие расчетно-аналитические методы определения значений границ полей допусков параметров технического состояния основаны в основном на аппроксимации многомерной области работоспособности вписанным в нее гипербрусом, проекции которого на оси пространства состояний объекта позволяют задавать независимые поля допусков на параметры технического состояния [1, 5, 6]. При таком подходе минимизируется вероятность нахождения оборудования в состоянии скрытого параметрического отказа, однако формируются дополнительные потери из-за простоев на регулирование параметров, обусловленные принудительным сужением границ области работоспособности при проведении аппроксимации.
Представляется целесообразным при определении границ поля допуска комплексно учитывать два вида ущерба – возможный ущерб в виде потерь качества продукции от нахождения оборудования в состоянии скрытого параметрического отказа и возможный ущерб от простоев в выпуске продукции, обусловленный необходимостью периодического регулирования параметров технического состояния.
Обобщенный (суммарный) ущерб является в данном случае интегральным показателем качества функционирования промышленного оборудования непрерывного использования и напрямую зависит от погрешности определения граничных значений полей контрольных допусков параметров технического состояния элементов оборудования. При оценивании величины обобщенного ущерба должны учитываться как величина абсолютного значения погрешности, так и ее знак. Так, при положительной погрешности составляющая ущерба обусловлена снижением качества выпускаемой продукции из-за возможности функционирования оборудования в состоянии скрытого параметрического отказа. При отрицательной погрешности составляющая ущерба возникает по причине уменьшения объема произведенной продукции из-за вынужденных перерывов функционирования для избыточного регулирования параметров технического состояния.
В связи с отмеченным выше представляется важным и актуальным решение проблемы определения границ области допустимых значений погрешности задания контрольных допусков (диапазона допустимой погрешности определения контрольных допусков) на основе учета величины обобщенного ущерба.
Пути решения проблемы
Проанализируем процесс функционирования промышленного оборудования непрерывного использования, которое в дальнейшем будем называть объектом контроля (ОК), при следующих допущениях.
Техническое состояние ОК определяется по результатам контроля группы параметров технического состояния (ПТС)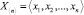 
, n – число ПТС. Все параметры статистически независимы. Контроль параметров технического состояния непрерывный. Изменение значений ПТС во времени – монотонное, возрастающее. На каждый параметр задано значение верхней границы поля контрольного допуска (ГПКД) xнi. В начале эксплуатации и после окончания регулировки значение параметра равно его номинальному значению xномi. ОК функционирует на интервале времени [0, t], на котором возможны регулировки значений параметров в случае достижения ГПКД. На интервале [0, t] размещается целое число NC циклов обслуживания ОК (циклом обслуживания будем считать суммарное время нахождения ОК в работоспособном состоянии и примыкающим к нему состоянии регулирования ПТС).
Рассмотрим вначале случай с единственным ПТС. Для данного варианта изменение ПТС во времени можно представить в виде случайной пилообразной функции, показанной на рис. 1.
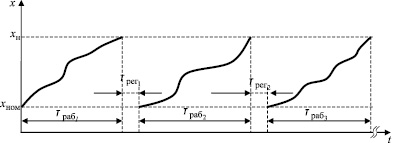
Рис. 1. Изменение значений периодически регулируемого параметра технического состояния объекта контроля во времени
Из рис. 1 видно, что на интервале [0, t] функционирование ОК периодически прерывается на проведение регулировок ПТС с целью приведения его к номинальному значению.
Назовем коэффициентом простоя ОК KП(t) долю времени, определенную на интервале [0, t], в течение которого объект не используется по прямому назначению вследствие проведения на нем мероприятий по регулировке ПТС.
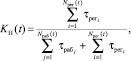
Выражение для коэффициента простоя ОК можно записать в следующем виде:
(1)
где Nрег – число интервалов регулировок; Nраб – число интервалов работы ОК на интервале [0, t].
С учетом сделанного выше допущения можно записать, что Nрег = Nраб = NC. Тогда выражение (1) преобразуется к виду
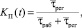
где 
– средняя длительность регулировки ПТС;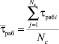 
– средняя длительность нахождения в работоспособном состоянии за один цикл обслуживания ОК.
Принимая во внимание, что процедура регулировки ПТС обычно слабо зависит от случайных факторов, так как выполняется подготовленным штатным персоналом по одним и тем же технологическим картам, можно полагать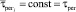 
. Тогда можно записать
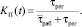(2)
Определим, каким образом погрешность задания границы поля контрольного допуска x влияет на коэффициент простоя KП(t).
Погрешность может быть вычислена как x = xн – x0, где xн – назначенное (установленное в документации) значение верхней ГПКД параметра x, а x0 – истинное значение данной границы. В зависимости от соотношения значений xн и x0 значение погрешности x может быть как положительным, так и отрицательным
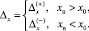
Положительный знак погрешности свидетельствует о том, что фактическая ГПКД смещена относительно истинной в сторону расширения поля допуска. Такое смещение ГПКД, с одной стороны, приводит к уменьшению коэффициента простоя, так как увеличивается средняя длительность нахождения в работоспособном состоянии за один цикл обслуживания ОК. С другой стороны, при положительной погрешности с течением времени возникает возможность достижения параметром технического состояния зоны скрытого параметрического отказа, т.е. при x(t) [x0, xн] ОК считается работоспособным, хотя фактически достигнуто состояние параметрического отказа, при котором параметры в качества продукции, производимой ОК, не полной мере удовлетворяют требованиям. Такое состояние в теории статистического контроля качества продукции называют ошибкой 2-го рода.
При отрицательной погрешности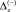 
вероятность ошибки 2-го рода равна нулю, однако появляется ошибка 1-го рода, когда при x(t) [xн, x0] ОК считается отказавшим и производится регулировка ПТС, хотя в действительности в данной ситуации параметрического отказа нет.
Если бы цена ошибок первого и второго рода была одинаковой при равенстве модулей погрешносте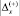й 
и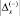 
, оптимальным вариантом с точки зрения минимума обобщенного ущерба был бы вариант xн = x0, т.е. с нулевой погрешностью x = 0. В действительности же, как правило, функция потерь не симметрична, при этом ущерб при равенстве модулей погрешносте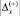й 
и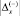 
не одинаков. В этой ситуации для минимизации обобщенного ущерба целесообразно смещать назначаемую ГПКД относительно x0, т.е. применять вариант с xн x0. Величина и знак смещения при этом зависит от соотношения потерь.
Рассмотрим далее возможность получения модельных соотношений, позволяющих определить величину и знак целесообразного смещения назначаемой ГПКД относительно x0.
В выражении (2) от x зависит только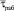 
– средняя длительность нахождения в работоспособном состоянии за один цикл обслуживания ОК. С учетом этого можно записать
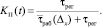(3)
Для определения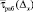 
представим изменение математического ожидания ПТС линейной функцией вида (рис. 2):
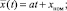
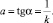(4)
Рассмотрим вначале ситуацию с расширением ГПКД, т.е. когда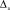 
= 
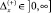. При расширении ГПКД имеем
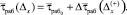(5)
Подставив (5) в (3), и с учетом того, что
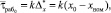
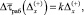
получим
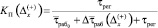
или
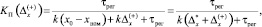(6)
где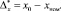 
В ситуации с сужением ГПКД относительно x0, когда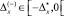 
, аналогично (6) имеем
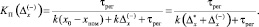(7)
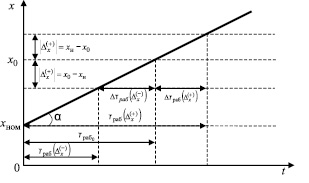
Рис. 2. Линейная аппроксимация изменения математического ожидания параметра технического состояния объекта контроля
Выражения (6) и (7) можно объединить, представив следующим образом:
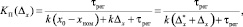(8)
где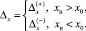 
Заметим, что при xн = x0·x и выражение (8) преобразуется к виду
График зависимости коэффициента простоя ОК от погрешности x представ- лен на рис. 3.
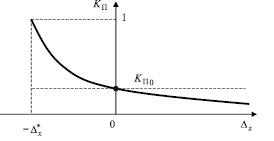
Рис. 3. Зависимость коэффициента простоя объекта контроля от погрешности x
Теперь можно рассчитать суммарный за время t ущерб от простоя при погрешности задания контрольного допуска, равной x, как
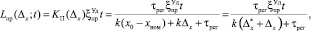(9)
где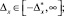 
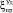– средние удельные потери от нахождения ОК в состоянии простоя.
Суммарный за время t ущерб от нахождения в состоянии скрытого отказа при погрешности задания контрольного допуска, равной x, определяется на основе выражения
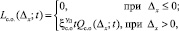(10)
где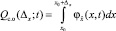 
– вероятность нахождения ОК в состоянии скрытого параметрического отказа; 
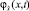– плотность распределения случайного процесса с функцией математического ожидания (4) в сечении t; 
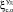– средние удельные потери от нахождения ОК в состоянии скрытого параметрического отказа.
Суммируя функции ущерба (9) и (10), можем представить обобщенный ущерб как
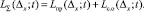
Рис. 4 иллюстрирует процесс определения границ области допустимых значений погрешности задания контрольных допусков (диапазона допустимой погрешности определения контрольных допусков) на основе учета величины обобщенного ущерба.
Минимальное значение обобщенного ущерба достигается 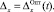при 
При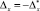 
значение обобщенного ущерба равно 
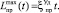При увеличении x величина обобщенного ущерба стремится к 
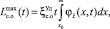причем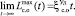 
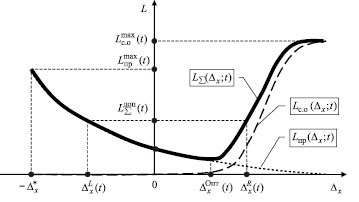
Рис. 4. Определение зависимости обобщенного ущерба от погрешности x
Если задать значение максимально допустимого обобщенного ущерба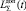 
на интервале [0, t], границы области допустимых значений погрешности задания контрольных допусков определяются как
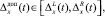
где
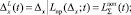(11)
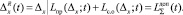(12)
Найдем аналитическое выражение для левой границы области допустимых значений погрешности задания контрольных допусков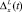 
.
Для этого составим уравнение
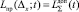
или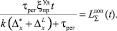 
После несложных преобразований получаем
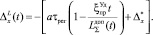(13)
Значение правой границы области допустимых значений погрешности задания контрольных допусков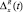 
является корнем уравнения
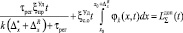(14)
или
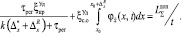(15)
В последнем случае задается допустимый средний удельный ущерб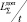 
и, исходя из его значения, определяется правая граница области допустимых значений погрешности 
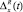. При нескольких ПТС 
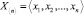на каждый параметр задаются свои значения верхней ГПКД xнi и определяются номинальные значения xномi. Рассчитываются величины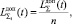 
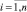максимально допустимых на интервале [0, t] значений обобщенного ущерба по всем параметрам технического состояния. Затем на основе выражений (11)–(15) определяются значения границ области допустимых значений погрешности задания контрольных допусков для каждого ПТС. И, наконец, вычисляются оптимальные по критерию минимума обобщенного ущерба значения погрешности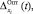 
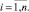
Выводы
Рассмотрены вопросы моделирования влияния погрешности задания граничных значений полей контрольных допусков на качество функционирования промышленного оборудования непрерывного использования. Показано, что в случае несимметричной функции потерь (неодинаковом ущербе при равных по модулю и противоположных по знаку погрешностях задания контрольных допусков) для минимизации обобщенного ущерба целесообразно смещать назначаемую границу поля контрольных допусков относительно ее истинного значения. Величина и знак смещения при этом зависит от соотношения ущербов от простоев и нахождения в состоянии скрытого отказа. Предложен способ определения границ области допустимых значений погрешности задания контрольных допусков, основанный на введении максимально допустимой величины обобщенного ущерба от погрешности задания допусков.