При работе бесчокерного трактора технологическая операция – подъём дерева стрелой манипулятора является основной и наиболее нагруженной [1, 2].
На рис. 1 представлена расчетная схема для исследования динамического нагружения бесчокерного трактора в этом режиме работы.
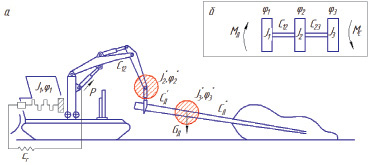
Рис. 1. Расчетная схема динамической системы «ВТМ – дерево»: а – исходная; б – эквивалентная
Принятые обозначения:
J1 – момент инерции кривошипно-шатунного механизма, маховика, сцепления и шестерён гидронасоса;
J2 – момент инерции манипулятора, захватного устройства, приведённый к коленчатому валу двигателя;
J3 – момент инерции предмета труда – дерева, приведённый к коленчатому валу;
φ1, φ2, φ3 – угловые перемещения масс соответственно с моментами инерции;
J1, J2, J3;
Сr – приведённая жесткость гидропередачи привода стрелы;
С12 – приведённая крутильная жесткость коленчатого вала, металлоконструкции манипулятора и гидропередачи поворота стрелы;
С23 – приведённая жесткость дерева;
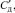
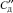– изгибные жесткости соответственно комлевой и вершинной частей дерева;
MC – приведённый момент сопротивления;
MД – крутящий момент, отбираемый от двигателя для привода гидронасоса;
fn – площадь поршня (поршней) гидроцилиндров привода стрелы;
P – давление в гидросистеме;
r – плечо силы Р (усилие на штоках гидроцилиндров привода стрелы);
L – вылет манипулятора.
Допущения:
1. Физико-механические свойства упругих связей постоянны.
2. Движения масс системы описываются линейными дифференциальными уравнениями с постоянными коэффициентами.
3. Величины L и r на пусковых режимах постоянны.
Кинетическая энергия системы:
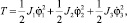
где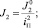 
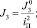
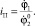
Потенциальная энергия системы:
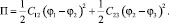
В соответствии с уравнением Лагранжа II рода система дифференциальных уравнений примет вид
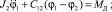
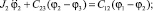(1)
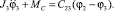
Полученную систему уравнений (1) дополним уравнением приведенной угловой скорости поворота манипулятора [1].
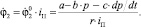
Кроме того, домножим уравнение (1) системы (1) на J2, а уравнение (2) на J1 и вычтем из первого второе, то есть
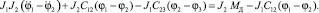(2)
В последнем приписанном уравнении к системе (1) обозначено
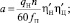
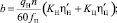
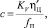
где qН – объёмная постоянная насоса; n – число оборотов вале насоса;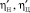 
– теоретические объемные КПД насоса с распределителем и гидроцилиндра; KV, KH, KЦ – коэффициенты пропорциональности; p – давление в гидронасосе; iП – передаточное число.
К уравнению (2) припишем уравнения (1), (3) и (4) системы (1):
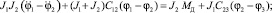
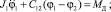
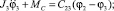
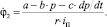(3)
Из уравнения (1) системы (3) выразим φ3:
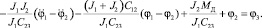
Из полученного выражения для 
выразим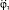 
:
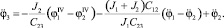
Полученные значения для φ3 и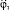 
подставим в уравнение (3) системы (3):
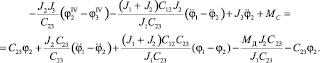(4)
Учитывая, что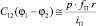 
[1, 2], определим p, 
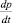и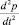 
, то есть
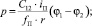
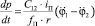
и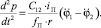 
(5)
Из уравнения (2) системы (3) выведем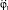 
и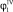 
:
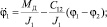
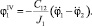
Значение (5) подставим в уравнение (4) системы (3):
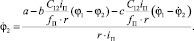
Отсюда:
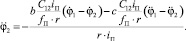
Значения для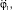 
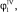
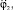
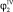подставим в уравнение (4) и преобразуем:
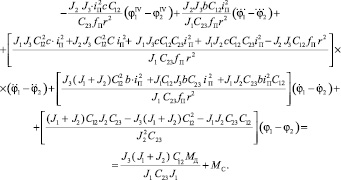(6)
Окончательно получим
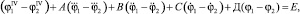(7)
где
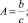
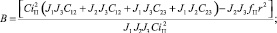
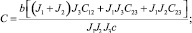
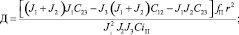
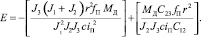
Уравнение (7) является неоднородным, и его решение будет состоять из частного решения и решения однородного уравнения, то есть Q = Q1 + Q2.
Частное решение представляет собой приведенную статическую деформацию упругой связи С12, то есть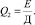 
Введя новую переменную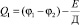 
, получим однородное дифференциальное уравнение вида
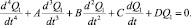(8)
Его характеристическое уравнение будет
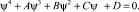(9)
Уравнение (9) имеет две пары комплексно-сопряжённых корней с отрицательными вещественными частями [3]:
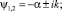
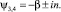(10)
В соответствие с этим решением однородного уравнения (8) будет
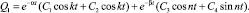
Начальными условиями для режима разгона системы будет:
при t = 0
Q1 = 0;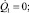 
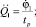
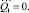
Пример.
Исходные данные примем применительно к бесчокерному трактору ТБ-1 [4, 5]:
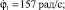J1 = 4,05 кг?м2; L = 5 м; v = 1 м/с;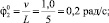 
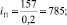
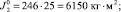
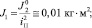fП = 153 см2;
С12 = 0,604 Н?м; V = 2,0 м3; H = 30 м; hТ = 12 м; GД = 20465 Н;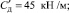 
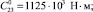
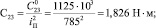
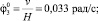
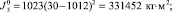
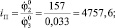
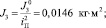
b = 1,57?10–6 м3/(с?Н); c = 0,275?10–6 м3/Н.
Определяем коэффициенты дифференциального уравнения (7):
A = 5,71 c–1; B = 369,61 c–2; c = 2099,75 c–2;
C = 2099,75 c–2; Д = 282,53 c–2.
1. Находим корни уравнения:
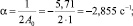
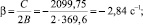
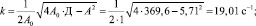
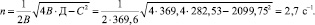
Таким образом, имеем
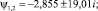
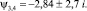
2. Используя выражения [3], находим значения произвольных постоянных C1...C4:
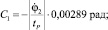
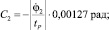C3 = –C1;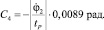 
3. Примем: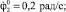 
время разгона – 0,25, то есть:
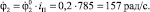
Тогда
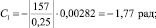C2 = –0,7975 рад; C3 = 1,77 рад; C4 = 5,589 рад.
На рис. 2 приведен график изменения деформации упругой связи «С12», построенный по приведенным расчетам.
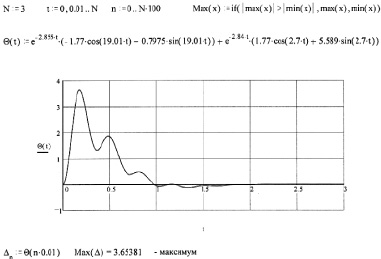
Рис. 2. График изменения деформации упругой связи «С12»
4. Определяем деформацию упругой связи и «С12» (рис. 2).
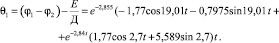
5. Находим максимальный динамический момент, воздействующий на силовую установку ВТМ:
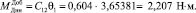
6. Суммарный момент на силовую установку будет равен
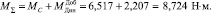
Здесь
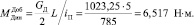
7. Снижение оборотов коленчатого вала произойдет
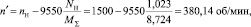
где
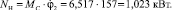
8. Коэффициент динамичности нагрузки определяется как
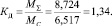
Выводы
1. Процесс подъема дерева стрелой манипулятора бесчокерного трактора сопровождается значительной динамической нагрузкой на силовую установку и приводит к предельно допускаемому для снижения частоты вращения коленчатого вала.
2. Для уменьшения нагруженности силовой установки в данном режиме работы необходимо снижать скорость пускового режима или увеличивать время разгона динамической системы.
3. Предложенная математическая модель позволяет определить нагруженность силовой установки трактора в режимах подъема-опускания дерева стрелой манипулятора на этапе разработки конструкторской документации.