На сегодняшний день с применением программируемой логики успешно реализуются архитектуры, типичные для суперЭВМ – лидеров мирового компьютеростроения. Программируемая логика служит прекрасной элементной базой для организации специфических вычислений, в частности нейросетевых, для реализации алгоритмов нечеткой логики и т.п. Отдельного внимания заслуживают широкий выбор использования вычислений: систем остаточных классов, арифметики рациональных дробей, различных систем счисления и много другого. Без особых сложностей на программируемых логических интегральных схемах (ПЛИС) аппаратно реализуются некоторые функции и алгоритмы с большим числом нестандартных операций, например с применением специфической битовой обработки. На многопроцессорных вычислительных средствах подобные операции реализуются крайне неэффективно [1].
Совместное использование ПЛИС (программируемые логические интегральные схемы) и СОК (система остаточных классов) позволяет ускорить основные операции цифровой обработки сигналов (ЦОС), таких как свертка, и за счет этого повысить производительность и обработку сигналов в режиме реального времени.
Система остаточных классов
Предположим, что система остаточных классов определена рядом L с положительными и попарными относительно главных целыми числами {m1, m2, ..., mi}. Эти числа называются модулями. Пусть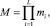 
тогда кольцо модуля целых чисел Z(M) представляет собой динамический диапазон системы остаточных классов. Следовательно, любое положительное целое число X ∈ Z(M) имеет единственное представление L = [x1, x2, ..., xL], где xL = X mod mi. Учитывая, что два целых числа X, Y∈ Z(M), и их соответствующие представления остатками [x1, x2, ..., xL] и [y1, y2, ..., yL], то арифметика в системе остаточных классов определена следующим образом:
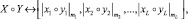(1)
где операция сложения, вычитание или умножение. Таким образом, арифметика СОК определена по прямой сумме кольца модуля целого числа mi, Z(mi) и выполняется параллельно без зависимости между остатками чисел [6].
Преобразование от представления остатка [x1, x2, ..., xL] к X – целому числу основано на китайской теореме об остатке.
Теорема. Если числа a1, a2, ..., an попарно взаимно просты, то для любых остатков r1, r2, ..., rn таких, что 0 ≤ ri < ai при всех i = 1, 2, ..., n, найдётся число N, которое при делении на ai даёт остаток ri при всех i = 1, 2, ..., n.
Таким образом, СОК обеспечивает фундаментальную методологию для разделения больших диапазонов динамических систем на множество меньших независимых каналов, по которым вычисления выполняются параллельно [5].
Линейная свертка
Существуют многочисленные алгоритмы ЦОС как общего типа для сигналов в их классической временной форме (телекоммуникации, связь, телевидение и пр.), так и специализированные в самых различных отраслях науки и техники (геоинформатике, геологии и геофизике, медицине, биологии, военном деле, и пр.). Однако все эти алгоритмы, как правило – блочного типа, построены на сколь угодно сложных комбинациях достаточно небольшого набора типовых цифровых операций, к основным из которых относятся свертка, корреляция, фильтрация, функциональные преобразования, модуляция.
Линейная свертка – основная операция ЦОС, особенно в режиме реального времени. Для двух конечных причинных последовательностей h(n) и y(k) длиной соответственно N и K свертка определяется выражением
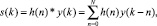(2)
где * – символьные обозначения операции свертки. Как правило, в системах обработки одна из последовательностей y(k) представляет собой обрабатываемые данные (сигнал на входе системы), вторая h(n) – оператор (импульсный отклик) системы, а функция s(k) – выходной сигнал системы. В компьютерных системах с памятью для входных данных оператор h(n) может быть двусторонним от –N1 до +N2, например – симметричным h(–n) = h(n), с соответствующим изменением пределов суммирования в (2), что позволяет получать выходные данные без сдвига фазы частотных гармоник относительно входных данных. При строго корректной свертке с обработкой всех отсчетов входных данных размер выходного массива равен K + N1 + N2 – 1 и должны задаваться начальные условия по отсчетам y(k) для значений y(0 – n) до n = N2 и конечные для y(K + n) до n = N1.
Рассмотрим пример выполнения дискретной свертки в среде программирования MATHCAD.
Преобразование свертки однозначно определяет выходной сигнал для установленного значения входного сигнала при известном импульсном отклике системы. Обратная задача деконволюции – определение функции y(k) по функциям s(k) и h(n), имеет решение только при определенных условиях. Это объясняется тем, что свертка может существенно изменить частотный спектр сигнала s(k) и восстановление функции y(k) становится невозможным, если определенные частоты ее спектра в сигнале s(k) полностью утрачены.
КИХ-фильтры
Одним из видов линейных цифровых фильтров, характерной особенностью которого является ограниченность по времени его импульсной характеристики (с какого-то момента времени она становится точно равной нулю) является фильтр с конечной импульсной характеристикой (КИХ-фильтр).
Из всего вышесказанного следует, что КИХ-фильтры могут быть осуществлены с помощью свёртки сигнала, т.е.
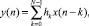(3)
где x(n) и y(n) – вход и выход фильтра; hk – коэффициенты фильтра; N – длина фильтра.
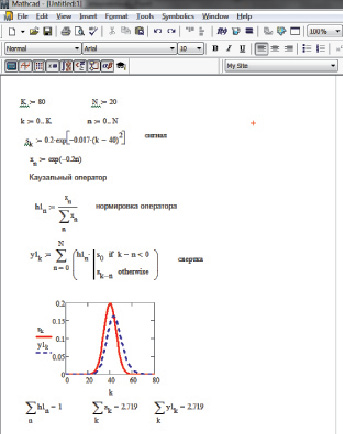
Рис. 1. Пример выполнения дискретной свертки с каузальным оператором в среде программирования MATHCAD
К основным операциям фильтрации информации относят операции сглаживания, прогнозирования, дифференцирования, интегрирования и разделения сигналов, а также выделение информационных (полезных) сигналов и подавление шумов (помех). Основными методами цифровой фильтрации данных являются частотная селекция сигналов и оптимальная (адаптивная) фильтрация.
Итак, если (3) перевести в СОК, то уравнение примет вид
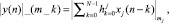
j = 1, 2, ..., L, (4)
где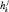 
и xj(n – k) обозначают остатки hk и xj(n – k) по модулю mj. Каждый модуль mj в (4) для j = 1, 2, ..., L функционирует независимо. Таким образом, для реализации каждого фильтра по модулю необходимо N множителей и N – 1 сумматоров. Использование распределенной арифметики позволяет уменьшить количество конфигурируемых логических блоков программируемых логических интегральных схем за счет использования системы остаточных классов [6].
На рис. 3 показана блок-схема фильтра, который в таком виде широко известен как трансверсальный (z-задержка на один интервал дискретизации).
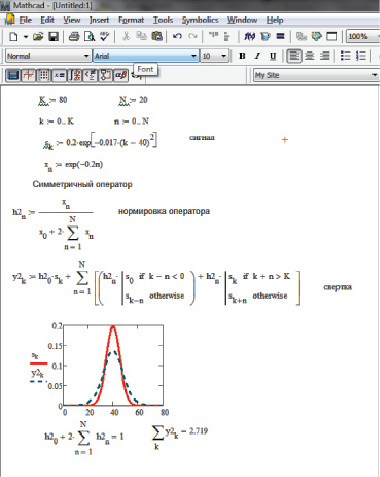
Рис. 2. Пример выполнения дискретной свертки с симметричным оператором в среде программирования MATHCAD
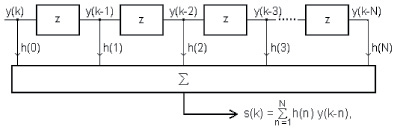
Рис. 3. Трансверсальный цифровой фильтр
Разработка устройств ЦОС повышенной пропускной способности на основе ПЛИС
Устройства программируемых логических интегральных схем обеспечивают потенциальные решения для системы остаточных классов, базирующейся на МАС-алгоритмах. Эти устройства состоят из логических элементов. В зависимости от группы, каждый логический элемент включает один или более переменных на входе программируемых логических интегральных схем.
Сложные логические операции и управление были первыми задачами, для решения которых, собственно, и создавались ПЛИС. В качестве иллюстрации возможностей ПЛИС в данной области рассмотрим пример реализации на программируемой логике ускоренной обработки XML-запросов.
В настоящее время в информационных системах сбора и обработки больших объемов данных для хранения информации в электронном виде стандартом является формат XML (Extensible Markup Language). Для навигации по XML-дереву и обращения к его элементам разработан специальный язык – XPath (XML Path Language). Суть задачи в упрощенном виде может быть сформулирована следующим образом. На сервере хранится большой документ в формате XML. От удаленных пользователей поступает интенсивный поток XPath-запросов. Необходимо для каждого запроса в реальном масштабе времени по известному алгоритму вычислить путь адресации, выбрать из имеющейся базы необходимые данные и сформировать результирующий XML-документ.
Данный процесс можно разделить на два последовательных этапа – синтаксический анализ и фильтрацию. Известное решение данной проблемы основано на кластеризации запросов, то есть на их группировке по сходным признакам с целью сузить область поиска в пространстве элементов. Но реализация данного подхода на кластерной архитектуре приводит к интенсивным обменам между процесссорными элементами. Возникает противоречие: параллельная по своей природе задача обработки большого количества независимых запросов становится тесно связанной, из-за чего теряются все преимущества кластеризации. Ситуация выглядит совершенно иначе при решении той же задачи на программируемой логике.
Для реализации вышеупомянутого подхода в реконфигурируемой структуре ПЛИС синтезируются цифровые автоматы, на состояния которых отображаются элементы пользовательских запросов. Собственно кластеризация осуществляется накапливанием многих запросов в одном цифровом автомате путем анализа элементов XPath-сообщений и обнаружения схожих путей адресации. За счет однообразия, а также использования априорно известной информации о запросах, анализ и кластеризацию удается выполнить до начала процесса фильтрации. В результате синтаксический анализатор и фильтр, представляющий собой большую комбинационную схему, также могут функционировать как две независимые ступени конвейера. Следует заметить, что схема фильтра, синтезируемая в ПЛИС, оптимизируется специальными программными средствами под конкретный XML-документ, хранящийся на сервере. Таким образом, достигается беспрецедентная степень адаптации вычислительной структуры к решаемой задаче, принципиально невозможная для микропроцессорных систем. Как следствие, в практических разработках удается достичь ускорения более чем на порядок по сравнению с традиционными подходами [4].
Заключение
Применение программируемых логических интегральных схем позволяет повысить производительность модульных арифметических процессоров цифровой обработки сигналов. Это приводит к слиянию систем остаточных классов и программируемых логических интегральных схем и позволяет достигнуть требуемой точности вычислений [2].
Совместное использование системы остаточных классов и современных программируемых логических интегральных схем обеспечивает высокую точность и пропускную способность выполнения двух операций: сложение и умножение, используемых при цифровой обработке сигналов реального времени.