В настоящее время широкое применение для линейных измерений находят измерители, в основе которых лежит использование оптических комбинационных полос, получаемых при оптическом сопряжении двух растров или дифракционных решеток [5]. Выделяют два типа комбинационных полос – муаровые, получаемые сопряжением растров, развёрнутых на малый угол, и нониусные, получаемые сопряжением растров с параллельными штрихами и разным шагом. Муаровые полосы более распространены, так как они менее чувствительны к погрешностям изготовления растров. Применение комбинационных полос позволяет значительно увеличить точность и чувствительность измерителей линейных перемещений. Так, погрешность измерителя линейных перемещений на голографических решетках Л-200 не превышает 0,16 мкм в диапазоне 200 мм [6].
Недостатками таких измерителей являются достаточно сложная конструкция и жесткие требования к растрам. Поэтому в работе [7] была сделана попытка упростить конструкцию измерителя, применяя цифровые муаровые полосы, получаемые сложением изображений растра при его сдвигах относительно приемника. Недостатком предложенного метода оказалась сложность выделения муаровой картины из полученного изображения, что привело к большой погрешности измерения и низкой скорости работы измерителя.
Нами было предложено использовать нониусные полосы, получаемые вычитанием изображений двух периодических структур с синусоидальным распределением интенсивности, имеющих разный период [4]. Разностное изображение содержит только две гармоники, одна из которых описывает нониусную систему полос, а вторая может быть легко устранена.
Результаты теоретических исследований
В работе [4] были проведены исследования, показавшие возможность формирования цифровых нониусных полос при вычитании изображений дифракционных картин, полученных от источников с разными длинами волн λ1 и λ2. Распределение интенсивности в разностном изображении будет
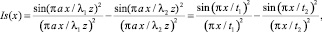(1)
где a – ширина щели, на которой происходит дифракция; z – расстояние от щели до приемника; t1 и t2 – периоды дифракционных картин. Знаменатель выражения (1) может быть исключен из расчетов, так как он не влияет на период дифракционной картины и может быть устранен на этапе цифровой обработки. Тогда выражение (1) примет вид
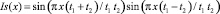. (2)
Анализ выражения (2) показывает, что оно содержит комбинационные полосы с шагом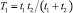 
и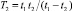 
. Для выделения полос с шагом T2, которые являются огибающими для полос с шагом T1, можно воспользоваться преобразованием Гильберта.
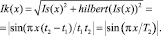(3)
Результат выделения огибающей приведен на рис. 1.
При сдвиге изображения дифракционной картины с периодом t2 на расстояние Δx смещение комбинационной полосы составит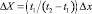 
, откуда коэффициент преобразования перемещения равен 
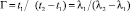. Отсюда следует, что в качестве опорного (неподвижного) изображения следует использовать дифракционную картину от источника с большей длиной волны λ1 > λ2.
Погрешность измерения сдвига изображения будет зависеть от погрешности дискретизации приемника, нестабильности длины волны излучения лазера и отношения сигнал-шум на фотоприемнике. Предельные значения частичных погрешностей измерения сдвига изображения, равного Δx = t2 = 400 мкм, при размере пиксела ПЗС приемника p = 3,2 мкм, отношении сигнал-шум S/N = 50, длинах волн источников λ1 = 632 нм и λ2 = 532 нм и нестабильности излучения δλ1 = δλ2 = 0,1 нм, составят соответственно
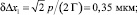
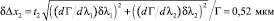
и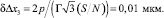 
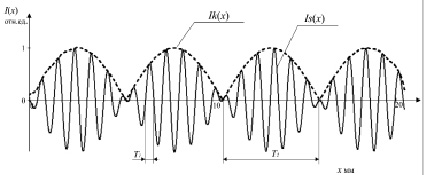
Рис. 1. Комбинационная полоса, возникающая при вычитании изображений дифракционных картин от источников с разными длинами волн
Отсюда следует, что сильное влияние на результат измерений оказывает нестабильность длин волн источников. Уменьшить влияние данных погрешностей можно, увеличив значение коэффициента преобразования.
Если смещение нониусной полосы превышает ее шаг T < ΔX, для устранения неопределённости измерения необходимо определить количество целых шагов, соответствующих этому сдвигу. Это возможно сделать, используя один из пикселов матричного приемника как марку, по которой измеряется целое количество периодов дифракционной картины, прошедших через нее. Тогда смещение изображения равно
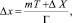(4)
где m – число целых периодов дифракционной картины, прошедших через марку. Если погрешность измерения шага комбинационной полосы
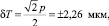
то погрешность измерения сдвига дифракционной картины Δx = ±5 мм (m = 12) будет равна
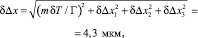
или 0,08 % измеряемой величины. При применении источников излучения с разностью длин волн порядка 10 нм коэффициент преобразования Г может принимать значения порядка 60–70, что приведет к уменьшению погрешности измерения до десятых долей микрона.
Результаты экспериментальных исследований
В работе [3] были предложены и экспериментально апробированы метод измерения линейных перемещений и функциональная схема измерителя, его реализующего, в основе которого лежит использование принципа работы датчика Шака – Гартмана [2]. Было сделано заключение, что основной вклад в погрешность измерения перемещения вносит погрешность дискретизации приемника, приводящая к большой погрешности измерения сдвига дифракционной картины. Для ее уменьшения было предложено применить описанный выше алгоритм формирования цифровых нониусных полос.
Для апробаций предложенного алгоритма был собран макет измерительной установки, изображённый на рис. 2. В качестве источников излучения были использованы полупроводниковые лазеры КЛМ-532 и КЛМ-632 мощностью 1 мВт и нестабильностью длины волны 0,5 нм. Для формирования сферической волны, освещающей щель, использовался микрообъектив ОМ-2, в фокальной плоскости которого была установлена точечная диафрагма диаметром 10 мкм. Щель шириной 0,4 мм была установлена на линейный транслятор, приводимый в движение микрометрическим винтом. Положение транслятора определялось с помощью датчика линейных перемещений, откалиброванного по концевым мерам 1-го класса точности и имеющего погрешность не более ±0,5 мкм в пределах измерительного диапазона ±100 мкм. В качестве приемника излучения использовалась ПЗС камера ToupCam с размером пиксела 3,2 мкм и диагональю 1/2 дюйма. Расстояние от точечной диафрагмы до щели составляло R = 110 мм, расстояние от щели до плоскости приемника z = 200 мм.
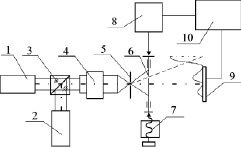
Рис. 2. Макет измерительной установки: 1 и 2 – лазерные модули КЛМ-532 и КЛМ-632; 3 – светоделитель; 4 – микрообъектив; 5 – точечная диафрагма; 6 – спектральная щель; 7 – линейный транслятор; 8 – измеритель линейных перемещений; 9 – ПЗС камера; 10 – блок регистрации и обработки данных (ПК)
Смещение щели было связано со смещением комбинационной полосы выражением
Δx = ΔX/Γ,
где Γ = Γ1Γ2;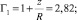 
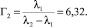
В ходе эксперимента щель смещалась в диапазоне 100 мкм с шагом 10 мкм. Перед началом измерений в память ПК записывалась опорная дифракционная картина от лазера КЛМ-632, из которой вычиталось изображение дифракционной картины от лазера КЛМ-532, соответствующее нулевому положению щели. Перед вычитанием оба изображения обрабатывались по алгоритму, описанному в работе [2] и включающему удаление высокочастотного аддитивного шума с помощью Фурье-преобразования, удаление фона изображения с помощью аналитической функции, построенной по минимумам дифракционной картины, и выравнивание контраста. После этого к полученному разностному изображению применялось преобразование Гильберта.
После сдвига щели смещенное дифракционное изображение вычиталось из опорного и строилась вторая система нониусных полос. Разность минимумов нониусных полос давала величину ΔX, соответствующую ее смещению. Экспериментально полученные цифровые полосы для нулевого положения щели и при ее смещении на 10 мкм приведены на рис. 3. В таблице приведены результаты измерения величины перемещения щели.
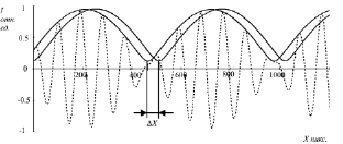
Рис. 3. Экспериментально полученные цифровые комбинационные полосы, соответствующие исходному и смещённому на 10 мкм положению щели
Результаты измерения смещения объекта
|
Задаваемые значения перемещения объекта в виде щели, мкм |
|||||||||
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
Экспериментально измеренные с помощью комбинационных полос перемещения объекта, мкм (однократное измерение) |
|||||||||
|
9,35 |
19,73 |
29,78 |
39,24 |
49,91 |
59,76 |
69,68 |
79,67 |
89,59 |
99,48 |
|
Экспериментально измеренные непосредственно по смещению дифракционной картины перемещения объекта, мкм (однократное измерение) |
|||||||||
|
8,66 |
19,08 |
29,17 |
38,90 |
49,05 |
58,75 |
68,77 |
78,70 |
88,55 |
98,50 |
График погрешности функционирования макета установки приведен на рис. 4. Максимальное экспериментальное значение погрешности составило 0,76 мкм. Расчетное значение предельной погрешности на границе измеряемого диапазона оценивалось из выражения
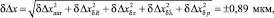
где δΔxδдат – погрешность измерения перемещения столика транслятора; δΔxδR – погрешность, обусловленная погрешностью установки щели относительно точечной диафрагмы (δR = ±0,5 мм); δΔxδz – погрешность, обусловленная погрешностью установки приемника относительно щели (δz = ±0,5 мм); δΔxδλ – погрешность, обусловленная нестабильностью длины волны полупроводникового лазера; δΔxδp – погрешность дискретизации приемника.
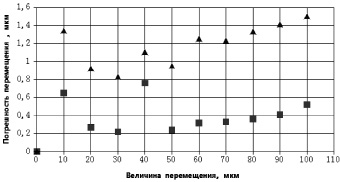
Рис. 4. График зависимости погрешности измерения перемещения щели от величины перемещения: комбинационной полосы (квадратные маркеры), непосредственно по дифракционной картине (треугольные маркеры)
Заключение
Предложенный метод измерения линейных перемещений, основанный на применении цифровых нониусных полос, позволяет значительно увеличить точность и чувствительность проводимых измеренийя. Проведенные расчеты и экспериментальные исследования показывают, что при оптимальном выборе параметров измерительной схемы возможно проводить измерения сдвига изображения с погрешностью порядка 0,08–0,05 % при условии, что нестабильность длины волны излучения источника не превышает 0,1 нм. Метод может быть использован для создания интерференционных и дифракционных измерителей линейных и угловых перемещений, позволяющих проводить измерения с субпиксельной точностью. При использовании источников излучения с близкими длинами волн, например 650 и 632 нм, применение цифровых комбинационных полос позволит оценивать сдвиг изображения на приемнике с погрешностью порядка 1/30 размера пиксела.