При распознавании речи в первую очередь необходимо разбить ее на слова. Упростим задачу: пусть речь содержит в себе паузы (промежутки между словами), которые будут разделять слова. В этом случае нужно понять величину порога – значения, выше которого элемент сигнала является словом, а все, что ниже, – паузой между словами [2].
Энтропией будем считать меру беспорядка, меру неопределенности. В нашем случае энтропия показывает, как сильно осциллирует сигнал в пределах конкретного фрейма. Фреймом является малый отрезок, на которые мы разделяем исследуемый сигнал, следует указать, что фреймы идут не друг за другом, а накладываются. Для подсчета энтропии пронормируем сигнал, построим график плотности распределения значений сигнала в пределах одного фрейма, а энтропию рассчитаем следующим образом:
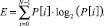 (1)
(1)
Для того чтобы отделить звук от тишины, её нужно с чем-то сравнивать. Опытным путем была подобрана величина порога, равная (0.1).
Таким образом, на вход нашей системы подается звуковой сигнал. Звук делится на фреймы – участки по 25 мс с перекрытием фреймов равным 10 мс. Для обработки звукового сигнала его следует преобразовать либо в виде спектра сигнала, либо в виде прологарифмированного спектра, с последующим масштабированием, поскольку это соответствует особенностям человеческого восприятия звука (Mel-шкала). Затем сигнал представляется в виде MFCC (Мел кепстральные коэффициенты) путем применения дискретного косинусоидального преобразования. MFCC обычно является вектором из тринадцати вещественных чисел, он представляют собой энергию спектра сигнала. Данный метод учитывает волновую природу сигнала, mel-шкала выделяет наиболее существенные частоты, воспринимаемые человеком, а количество MFCC коэффициентов можно задать любым числом, что позволяет сжать фрейм и уменьшить количество обрабатываемой информации [3].
Рассмотрим алгоритм MFCC-преобразования получаемого звукового сигнала.
Получаемый звуковой сигнал дискретизируется:
x[n], 0 ≤ n < N. (2)
Представляем его в качестве Фурье преобразования:
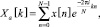 0 ≤ k < N. (3)
0 ≤ k < N. (3)
Рассчитываем гребенку фильтров, используя окно:
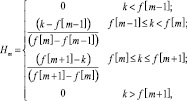 (4)
(4)
где f[m] будет равно
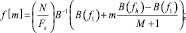 (5)
(5)
В(b) – представляем наши частоты в виде Мел-шкалы:
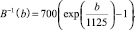 (6)
(6)
Где энергия окон будет равна
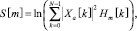
0 ≤ m < M. (7)
Получаем коэффициенты MFCC [4]:
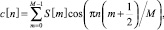
0 ≤ n < M. (8)
Пусть наш фрейм представляется в виде дискретного вектора значения согласно формуле (2).
Вычислим спектр сигнала:
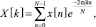 0 ≤ k < N. (9)
0 ≤ k < N. (9)
Обработаем сигнал окном Хэмминга, чтобы сгладить пульсации сигнала на краях [6].
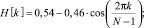 (10)
(10)
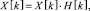 0 ≤ k < N. (11)
0 ≤ k < N. (11)
По оси ОХ откладывается частота в Герцах, по оси ОY – магнитуда, чтобы не связываться с комплексными величинами (рис. 1):
Mel представление показывает значимость отдельных частот звука для человека, зависит и от конкретных частот звука, и от громкости, и от тембра человека. Mel-шкала вычисляется следующим образом (прямое и обратное преобразование):
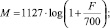 (12)
(12)
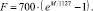 (13)
(13)
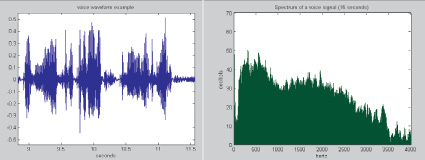
Рис. 1. Представление исходного сигнала в качестве Фурье преобразования
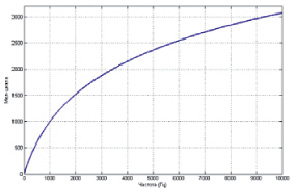
Рис. 2. График зависимости Мел-шкалы от частоты
График зависимости Мел-шкалы от частоты представлен на рис. 2.
Наибольшее распространение в системах распознавания речи получили именно эти единицы измерения, поскольку они соответствуют особенностям восприятия звука человеком.
Рассмотрим пример: дан фрейм длиной 256 отсчетов (выборок), частота звука 16 кГц. Пусть человеческая речь сосредоточена в диапазоне частот от 300 Гц до 8 кГц. Наиболее часто используемое количество Mel-коэффициентов равно десяти, его и будем использовать.
Сначала необходимо рассчитать гребенку фильтров, чтобы представить спектр в формате mel-шкалы. Мел-фильтр является треугольным окном, которое суммирует энергию на своем диапазоне частот и вычисляет mel-коэффициенты. Поскольку мы знаем количество коэффициентов, то сможем построить набор из десяти фильтров (рис. 3).
В области низких частот (те частоты, которые нам наиболее интересны) количество окон больше, что обеспечивает высокое разрешение. Это позволяет существенно повысить качество распознавания.
Для того чтобы найти энергию сигнала, перемножим вектор спектра сигнала и функцию окна, в результате чего получим вектор коэффициентов. Если их возвести в квадрат, представить в виде логарифма и получить из них кепстральные коэффициенты, то получим искомые mel-коэффициенты. Кепстральные коэффициенты можно получить как с помощью Фурье-преобразования, так и с помощью дискретного косинусоидального преобразования [6].
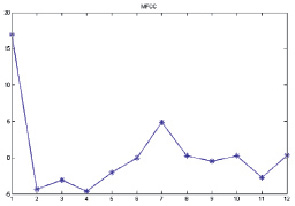
Рис. 3. Mel-частотные кепстральные коэффициенты
Диапазон частот составляет от 300 Гц до 8 кГц. На mel-шкале этот диапазон соответствует от 401,25 до 2834,99. Теперь строим двенадцать опорных точек для постройки десяти треугольных фильтров (Мел-шкала и шкала в герцах):
 (14)
(14)
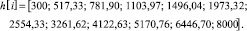 (15)
(15)
Как мы уже говорили, длина фрейма составляет 256 отсчетов сигнала, частота 16 кГц (откладывается по оси ОХ). Наложим рассчитанную шкалу на спектр сигнала.
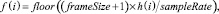 (16)
(16)
что соответствует
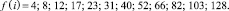 (17)
(17)
По опорным точкам построим фильтры:
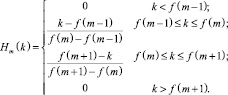 (18)
(18)
Фильтр перемножается со спектром:
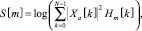
0 ≤ m < M. (19)
Мел-фильтры применяются к энергии спектра, затем полученные значения логарифмируются.
Дискретное косинусоидальное преобразование (ДКТ) применяется для получения кепстральных коэффициентов, оно сжимает полученные результаты, повышает вклад первых коэффициентов и понижает вклад последних.
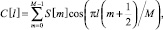
0 ≤ l < M. (20)
Получается, что у нас имеется 12 коэффициентов (рис. 3):
В итоге небольшой конечный набор значений (например, двенадцать коэффициентов в нашем случае) позволяет заменить использование огромного числового массива отсчетов сигнала, либо спектра сигнала, либо периодограммы сигнала.
Каждому слову конечной длины соответствует набор мел-частотных кепстральных коэффициентов. Затем необходимо найти наиболее близкую модель для определенного набора мел-частотных кепстральных коэффициентов. Для этого мы ищем евклидово расстояние между вектором мел-частотных кепстральных коэффициентов и вектором исследуемой модели. Искомой является та модель, у которой рассчитываемое расстояние наименьшее.
Набор MFCC коэффициентов для одного и того же слова может отличаться, например, в том случае, если слово произносится двумя разными людьми, либо скорость произношения отличается. Для этих целей используется алгоритм динамической трансформации времени. Он рассчитывает оптимальную деформацию времени между сравниваемыми временными последовательностями [2].
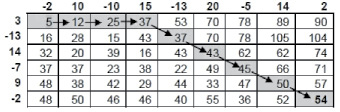
Рис. 4. Результаты расчетов
Допустим, у нас есть два числовых ряда (a1, a2, ..., an) и (b1, b2, ..., bm). Их длина может отличаться. Будем использовать Евклидово расстояние для расчета локальных отклонений между соответствующими элементами двух числовых рядов. В итоге получим матрицу отклонений N×M:
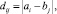
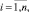
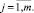 (21)
(21)
Критерий оптимизации для расчета минимального расстояния:
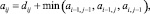 (22)
(22)
где aij – min расстояние между последовательностями (a1, a2, ..., an) и (b1, b2, ..., bm). Данный способ позволяет вычислить минимальную длину траектории движения от элемента а11 до элемента bnm (рис. 4).
Алгоритмы динамической трансформации времени полезны для распознавания отдельно стоящих слов при наличии словаря. В случае проблемы распознавания и обработки слитной речи гораздо более полезны СММ (скрытые марковские модели).
На основе представленного алгоритма разработано консольное приложение, позволяющее реализовать представленный алгоритм (рис. 5).
Для запуска приложения Sound необходимо вызвать командную строку при помощи RUN.BAT. Далее из командной строки вызываем команду: Sound -h. Возможны следующие вызовы команд: Список всех доступных моделей: Sound -l; Разделение источника в образцы: Sound -i samples/female1.wav -s_split; Добавление образца в модель: Sound -i samples/female1/1.wav -a odin; Распознавание образца: Sound -i samples/female1/1.wav -r; Модульные тесты: unit_tests --gtest_filter=MATH_MFCC.
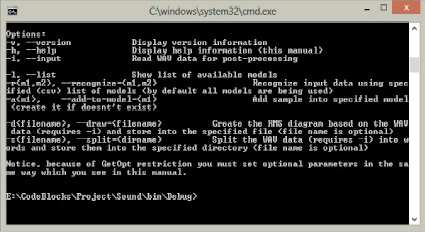
Рис. 5. Работа разработанной программы в командной строке
В первую очередь из main создается экземпляр класса Command Processor. Процессор создает команды, основанные на входных параметрах. Работа начинается вывода команды input. При этом происходит вызов метода Audio Data Command::read Data. При этом происходит запись данных в структуру wavData и поле wavData, класса context заполняется данными wavData. Данные очищаются от шумов, нормализуются.
Все этапы получения MFCC-коэффициентов выполняются в методе MFCC::transform().
Таким образом, принцип работы заключается в разбивке речи на слова на основе вычисления энтропии, эмпирическим методом было вычислено пороговое значение 0,1, затем идет разбивка на фреймы и вычисляются mel-коэффициенты. Затем идет сравнение со словарем. В качестве эксперимента брались записи слитной речи мужских и женских голосов, записанных в тихой комнате с отсутствующим шумом. Качество распознавания, показанное данным методом составило 75 %.



