Основные принципы расчёта характеристик пневматических упругих элементов с резино-кордными оболочками (РКО) при различных формах нагружения были изложены в работах В.Л. Бидермана и Б.Л. Бухина [1], которые можно считать основополагающими работами в этом направлении. Наиболее полное обобщение этих работ и дальнейшая разработка методов синтеза пневматических упругих элементов на базе существуюших резино-кордных оболочек выполнены в работе [3]. Разработанный метод расчёта геометрии направляющих поверхностей металлоарматуры упругих элементов с РКО и был положен в основу при разработке конструкции пневматического виброизолятора с РКО тороидного типа для систем вторичного подрессоривания.
В процессе эксплуатации подрессоренная кабина многоосного шасси совершает сложные пространственные движения. Пневматические упругие элементы с РКО тороидного типа в системе подвешивания кабины испытывают осевые, также продольные и поперечные внешние воздействия. На рис. 1 представлены схемы деформаций с РКО и перекатки её гофров, когда опорный элемент виброизолятора находится в крайних положениях, при нагружении его осевой и поперечной нагрузкой.
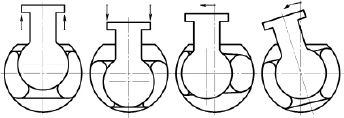
Рис. 1. Схемы деформации РКО при нагружении упругого элемента осевой, поперечной или угловой нагрузкой
Проведенные исследования по выбору типа упругого элемента для систем вторичного подрессоривания многоосных автомобилей позволили сформулировать основные технические требования, предъявляемые к пневматическому виброизолятору с РКО. Для пневматических систем вторичного подрессоривания многоосных автомобилей наиболее целесообразно применение РКО тороидного типа [5].
Пневматические упругие элементы с РКО тороидного типа хорошо компонуются в системах вторичного подрессоривания, осуществляют виброизоляцию как в осевом, так и в продольном и поперечном направлениях, обладают способностью воспринимать угловые и сложные нагрузки при полном отсутствии металлического контакта (жесткой связи). Наряду с этим пневмоэлементы с РКО тороидного типа позволяют совмещать в себе упругие и демпфирующие свойства. При этом регулирование взаимовлияния этих свойств за счёт варьирования конфигурацией поверхностей металлоарматуры, с которой оболочка находится в контакте, позволяет во многих случаях получить близкую к оптимальной, упруго-диссипативную характеристику подвески [6].
На рис. 2 представлен пневматический упругий элемент с РКО тороидного типа для систем вторичного подрессоривания автомобилей. Важной конструктивной особенностью этого упругого элемента является то, что нелинейный профиль направляющей арматуры позволяет получать требуемые характеристики жесткостей виброизолятора.
При линейной арматуре (конус, цилиндр и пр.) получить требуемые изменения жесткостей значительно сложнее по технологическим причинам и из-за несовместимости требований, предъявляемых к горизонтальным и осевым нагрузочным характеристикам.
На рис. 2 приняты следующие обозначения: 1 – корпус виброопоры, 2 – опорный элемент (поршень), 3 – РКО тороидного типа. При осевых перемещениях опорный элемент перемещается относительно корпуса, при этом деформируются и перекатываются по поверхностям металлоарматуры (корпус и опорный элемент) гофры эластичной оболочки. Изменение силы при изменении величины деформации упругого элемента обеспечивается в основном за счёт изменения эффективной площади, равной разности площадей Sэ1 и Sэ2, характеризуемых эффективными диаметрами Дэ1 и Дэ2 пневмоэлемента, при деформации гофров оболочки между поверхностями металлоарматуры, а также за счёт сжатия воздуха в РКО.
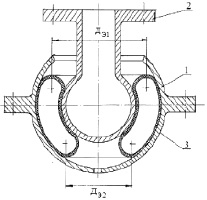
Рис. 2. Схема пневматического упругого элемента с РКО тороидного типа
При колебаниях с допустимыми амплитудами происходит деформация тороидной оболочки, сопровождаемая перекатыванием гофров, а также изменение воздушного объёма РКО. Такое конструктивное исполнение пневматического упругого элемента позволит обеспечить хорошие виброизолирующие свойства по всем направлениям колебаний.
Текущее значение усилия Q(x) на пневматический упругий элемент с РКО тороидного типа определяется по уравнениям
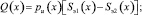 (1)
(1)
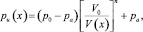 (2)
(2)
где pu(x) – текущее значение давления в РКО; Sэ1(x), Sэ2(x) – текущее значение эффективных площадей верхнего и нижнего гофров РКО тороидного типа; p0 – начальное (статическое) значение давления в РКО; pa – атмосферное давление; V0 – начальный объём внутренней полости РКО; V(x) – текущее значение объёма внутренней полости РКО; n – показатель политропы, зависящий от условий теплообмена между рабочим газом и окружающей средой.
Значение текущего объёма определяется после разбиения суммарного объёма на элементарные составляющие, объём которых вычисляется по теореме Гюльдена:
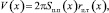 (3)
(3)
где Sп.п(x) – площадь поперечного сечения фигуры вращения; rц.т(x) – координаты центра тяжести фигуры вращения.
Дифференцируя по x уравнение (1), получим формулу для определения осевой жёсткости Cx пневмоамортизатора:
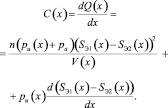 (4)
(4)
Эта формула показывает, что осевая жёсткость пневмоамортизатора определяется суммой двух слагаемых, из которых первое зависит от размеров пневматического упругого элемента (т.е. от величин Sэ1 и Sэ2) и от показателя политропы воздуха, а второе зависит ещё и от скорости изменения эффективного радиуса, то есть от формы направляющих поверхностей металлоарматуры. Геометрические параметры пневматического упругого элемента с РКО тороидного типа, влияющие на его характеристики, полностью определяются эффективными площадями Sэ1 и Sэ2 и V – внутренним объёмом РКО.
Эффективные площади для верхнего и нижнего гофров пневматического упругого элемента с РКО тороидного типа определяются из соотношений
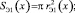
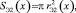 (5)
(5)
откуда
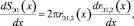 (6)
(6)
где rэ1,2 – эффективные радиусы верхнего и нижнего гофров пневмоэлемента с РКО тороидного типа.
Уравнения (1)–(6) позволяют выполнить расчёт осевых нагрузочных характеристик пневматического упругого элемента с РКО тороидного типа для различных начальных значений избыточного давления и объёма полости рабочего газа в РКО, если известны функции rэ1(x) и rэ2(x).
Расчётная схема для определения нагрузочной характеристики пневматического упругого элемента с РКО тороидного типа, у которого направляющая арматура (поршень и корпус) выполнены в виде сферических поверхностей, представлена на рис. 2.
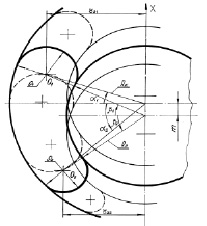
Рис. 3. Расчётная схема осевой нагрузочной характеристики пневматического упругого элемента с РКО тороидного типа
Система геометрических соотношений, характеризующих произвольное положение РКО упругого элемента при его осевой деформации, определится из решения треугольников O1O2K, O1O2M, O1KM, O2KM и уравнения постоянства длины профиля оболочки:
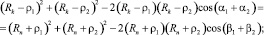 (7)
(7)
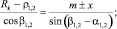
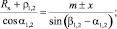
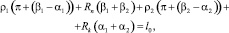
где l0 – длина профиля резино-кордной оболочки; ρ1 и ρ2 – радиусы гофров РКО; α1,2 – и β1,2 – углы наклона нормалей, проведённых в точках сопряжения гофра оболочки с направляющими поверхностями ограничивающей арматуры (корпуса и поршня) [7, 8].
После решения приближёнными методами системы из шести нелинейных трансцендентных уравнений (7) можно получить текущие значения переменных β1, β2, α1, α2, ρ1, ρ2. В зависимости от величины хода x упругого элемента. Эффективные радиусы пневматического упругого элемента rэ1(x) и rэ2(x) определяются из соотношений
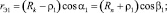 (8)
(8)
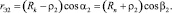 (9)
(9)
Значения текущего объёма с учётом (3) определяются из соотношений
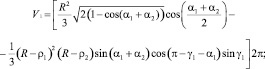 (10)
(10)
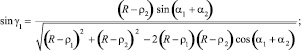 (11)
(11)
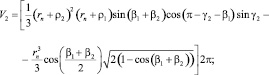 (12)
(12)
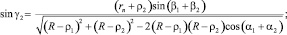 (13)
(13)
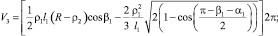 (14)
(14)
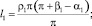 (15)
(15)
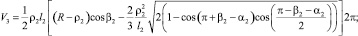 (16)
(16)
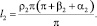 (17)
(17)
На рис. 4 представлена расчётная схема поперечного нагружения силой Qx пневматического упругого элемента с РКО тороидного типа. На схеме ось Y направлена вдоль линии действия силы Qx. При перемещении поршня характер деформирования стенки РКО меняется по мере её удаления от оси Y. Если провести радиальное сечение РКО под углом через ось симметрии поршня (рис. 4), то в левой фронтальной зоне поверхности РКО при φ = 0, радиальный профиль РКО испытывает максимальное сжатие, а в правой при φ = π – максимальное растяжение. При этом центры гофров О1 и О2 левого профиля РКО расходятся в стороны, а центры гофров P1 и P2 сближаются.
В боковых зонах упругого элемента, при φ = ±π/2, поверхность РКО испытывает максимальные сдвиговые деформации, при этом размеры радиальных профилей в этих зонах практически не меняются [3].
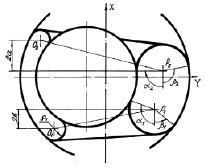
Рис. 4. Расчётная схема поперечной нагрузочной характеристики пневматического упругого элемента с РКО тороидного типа
Поэтому при поперечном ходе поршня упругого элемента Y происходит наклон эффективных площадей верхнего и нижнего гофров пневмоамортизатора на величину 2а и 2b соответственно. Сумма проекций эффективных площадей верхнего и нижнего гофров на плоскость, перпендикулярную линии действия поперечной силы, представляет собой поперечную эффективную площадь пневматического упругого элемента с РКО тороидного типа.
При расчёте поперечной нагрузочной характеристики ПУЭ с РКО тороидного типа принимаем, что поперечная эффективная площадь равняется сумме поперечных эффективных площадей верхнего и нижнего гофров, которые являются эллипсами с полуосями равными соответственно а и rэ, b и rэ или (а + b) и rэ:
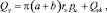 (18)
(18)
где Qyk – составляющая поперечная сила, обусловленная упругими свойствами стенки РКО. Величины rэ и pu в этой формуле определяются по осевому положению пневматического упругого элемента. Поперечная жесткость Сy пневматического упругого элемента с РКО тороидного типа равна
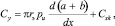 (19)
(19)
где
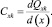 (20)
(20)
Аналитическое исследование поперечной жесткости требует весьма сложного математического аппарата для определения равновесного положения резино-кордной оболочки при поперечной деформации. При этом возникают задачи, связанные с необходимостью определения фактической геометрии кордного каркаса несимметрично деформированной оболочки и учета упругих свойств резины и корда. Решение этих задач приводит к громоздким трансцендентным выражениям с использованием интегралов, не берущихся в конечном виде.
Поэтому в инженерной практике используют приближенные формулы для расчёта поперечной жесткости. Для нашей расчётной схемы (рис. 4) будем рассчитывать поперечную жесткость для верхнего и нижнего гофров эластичной оболочки отдельно. Общая поперечная жесткость ПУЭ с РКО тороидного типа равна сумме 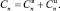 Ниже величина
Ниже величина 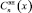 определяется по известной полуэмпирической формуле, учитывающей влияние как ограничивающей арматуры, так и геометрии каркаса РКО [2,4]:
определяется по известной полуэмпирической формуле, учитывающей влияние как ограничивающей арматуры, так и геометрии каркаса РКО [2,4]:
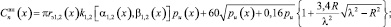 (21)
(21)
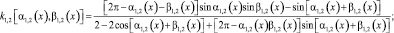 (22)
(22)
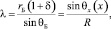 (23)
(23)
где pu(x) – текущее избыточное давление рабочего газа; θk(x) – угол, составленный направлением нити корда и меридианом РКО; rБ – радиус сборочного барабана; θБ – угол закроя корда; δ – коэффициент условной вытяжки корда.
В работе [4] построена номограмма, позволяющая определять параметры перекатывания гофровых РКО при поперечных деформациях, из которой видно, что при нелинейном профиле направляющей арматуры, обеспечивающей нелинейное изменение углов α(х) и β(х), можно получить любую характеристику жесткости виброопоры в поперечном направлении, варьируя параметры m, Rk, Rn.
Исследование влияния геометрических параметров пневматического упругого элемента с РКО тороидного типа на его нагрузочные характеристики подтверждает предположение о возможности создания пневмовиброизолятора для систем вторичного подрессоривания автомобилей с наперёд заданными желаемыми нелинейными характеристиками.



