Теория краевых задач для уравнений смешанного типа является одним из важнейших разделов современной теории дифференциальных уравнений с частными производными. Это обусловлено как непосредственными связями уравнений смешанного типа с проблемами теории сингулярных интегральных уравнений, теорией интегральных преобразований и специальных функций, так и прикладными задачами околозвуковой газовой динамики, теории бесконечно малых изгибаний поверхностей, магнитной гидродинамики, математической биологии и в других областях.
Цель исследования
Актуальным продолжением этих исследований является постановка и доказательство однозначной разрешимости задачи со смещением для уравнения смешанного эллиптико-гиперболического типа с перпендикулярными линиями параболического вырождения.
Постановка задачи. Рассмотрим уравнение смешанного типа
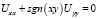 (1)
(1)
в конечной односвязной области D плоскости переменных 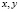 , ограниченной жордановой кривой А с концами в точках А(1,0), B(0,1), расположенной в первом квадранте x > 0, y > 0, и характеристиками BC: y – x = 1, CD: x + y = 0, DA: x – y = 1 уравнения (1).
, ограниченной жордановой кривой А с концами в точках А(1,0), B(0,1), расположенной в первом квадранте x > 0, y > 0, и характеристиками BC: y – x = 1, CD: x + y = 0, DA: x – y = 1 уравнения (1).
Обозначим через 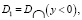
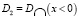 – гиперболические части смешанной области D, а через
– гиперболические части смешанной области D, а через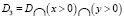 – эллиптическую часть,
– эллиптическую часть, 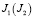 – интервал 0 < x < 1 (0 < y < 1) прямой y = 0 (x = 0).
– интервал 0 < x < 1 (0 < y < 1) прямой y = 0 (x = 0).
Задача. Найти регулярное в области D решение U(x, y) уравнения (1), удовлетворяющее краевым условиям:
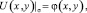 (2)
(2)
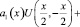
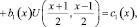 (3)
(3)
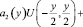
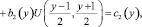 (4)
(4)
где φ(x, y), ai(t), bi(t), ci(t), – заданные непрерывные функции, причем
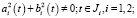
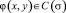 ,
, 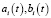 ,
,
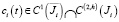 где h > 0.
где h > 0.
Под регулярным в области D решением уравнения (1) будет пониматься функция U(x, y) из класса 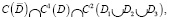 удовлетворяющая уравнению (1) и такая, что
удовлетворяющая уравнению (1) и такая, что 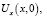
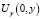 могут обращаться в бесконечность порядка ниже единицы на концах интервалов
могут обращаться в бесконечность порядка ниже единицы на концах интервалов 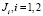 .
.
Задача (1)–(4) относится к классу краевых задач со смещением [6], исследованием которых для уравнений смешанного типа с одной и двумя линиями вырождения занимались многие авторы [1–10]. Подробная библиография работ содержится в [1, 6].
Единственность решения задачи. Положим,
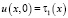 ,
, 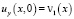 ; (5)
; (5)
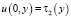 ,
, 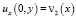 . (6)
. (6)
Решение задачи Коши (5) в области D1 для уравнения (1) имеет вид
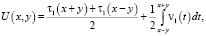 (7)
(7)
решение задачи (6) в области D2
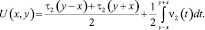 (8)
(8)
Удовлетворяя (7), (8) условиям (3), (4) с учетом
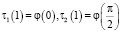 ,
,
будем иметь
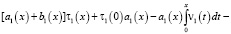
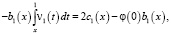 (9)
(9)
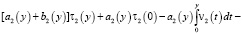
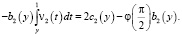 (10)
(10)
где 1(0) и 2(0) определяются из (3), (4):
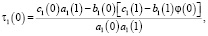
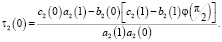
Соотношение между τi(t) и vi(t) из гиперболических частей D1 и D2 смешанной области D (9), (10) можно переписать в виде:
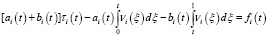 , (11)
, (11)
где при i = 1, t = x, при i = 2, t = y;
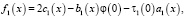
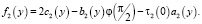
Теорема. В области D не может существовать более одного решения задачи (1)–(4), если выполнены условия:
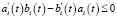 , (12)
, (12)
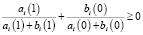 , (13)
, (13)
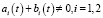 . (14)
. (14)
Действительно, интегрируя тождество
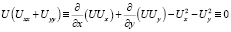
по области D3, получим соотношение
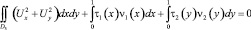 . (15)
. (15)
Полагая 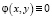 ;
; 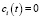 , докажем, что
, докажем, что
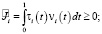 где
где 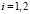 .
.
Действительно, пусть выполняется условие (14) теоремы единственности. Тогда (11) перепишем в виде
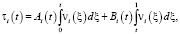
где
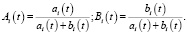
Рассмотрим
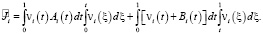
Принимая во внимание, что
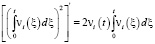 ,
,
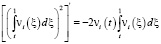 ,
,
будем иметь
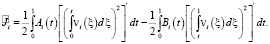
Последнее в результате интегрирования по частям примет вид:
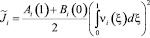
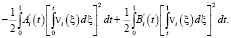
Легко видеть, что 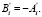 Таким образом, при выполнении условий (12), (13) теоремы единственности будет выполняться
Таким образом, при выполнении условий (12), (13) теоремы единственности будет выполняться 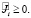
Отсюда следует единственность решения задачи.
Существование решения задачи. В области D3 рассмотрим задачу Холмгрена
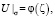
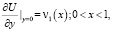
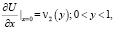
решение которой задается формулой [9]:
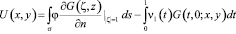
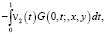 (16)
(16)
где n – внутренняя нормаль.
В случае, когда σ совпадает с дугой нормального контура х2 + y2 = 1, функция
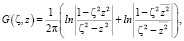
где
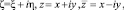
является функцией Грина задачи Холмгрена для решения уравнения (1) в области D3.
Полагая в (16) сначала y = 0, а затем x = 0, получаем
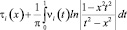
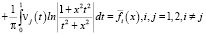 , (17)
, (17)
где
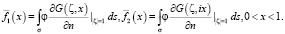
Равенства (17) являются функциональными соотношениями, принесенными из эллиптической части D3 смешанной области D на Ji. Соотношения из гиперболических частей смешанной области имеют вид (11).
Исключая τi(t) из (11), (17), для определения неизвестных функций vi(t) получим систему интегральных уравнений:
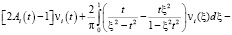
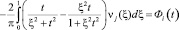 , (18)
, (18)
где
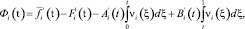
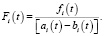
Система (18) путем замены неизвестных функций
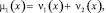
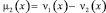
c учетом тождеств
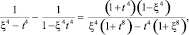
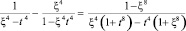
и замены переменных
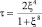 ,
, 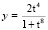
приводится к виду
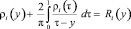 , (19)
, (19)
где
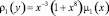 ,
,
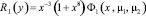 ,
,
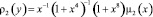 ,
,
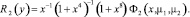
Решения системы (19) существуют и в требуемом классе функций и определяются формулами [5, 9]:
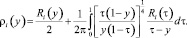
После определения неизвестных функций ρi(y) находятся v1(x) и v2(x). По найденным vi(x) определяются τi(t) из (11) и решение задачи (1)–(4) как решение задачи Холмгрена в D3 и решение задач Коши в D1 и D2.



