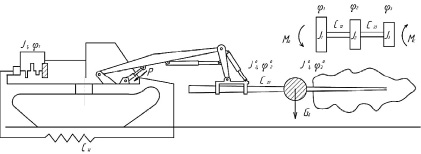
При разборе завалов леса часто возникают режимы аварийного торможения стрелы манипулятора при подъеме или спускании горизонтально расположенного дерева, вследствие чего происходят колебания масс динамической системы значительных амплитуд. На рису. 1 представлена расчетная схема системы «ВПМ – предмет труда – дерево» для исследования данного режима работы.
Кинетическая энергия системы
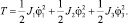
Потенциальная энергия системы
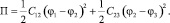
В выражении кинетической энергии
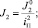
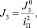
где iП – передаточное число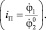 
В соответствии с уравнением Лагранжа II-го рода имеем следующую систему уравнений:
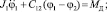
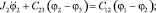(1)
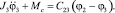
Домножим уравнение (1) системы (1) на J2, уравнение (2) на J1, уравнение (2) на J3 и уравнение (3) на J2 и соответственно вычтем из первого второе.
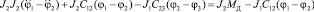
или
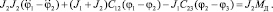(2)
аб
Рис. 1. Расчетная схема динамической системы «ВПМ – предмет труда – дерево»: а – исходная; б – эквивалентная. Принятые обозначения: J1 – приведённый момент инерции кривошипно-шатунного механизма, маховика и сцепления; J2, J3 – приведенные к коленчатому валу моменты инерции соответствующего манипулятора с ЗСУ и дерева; 1, 2, 3 – обобщенные угловые координаты масс соответственно с моментами инерции J1, J2, J3; С12 – крутильная жесткость коленчатого вала, гидропередачи и манипулятора; С23 – приведенная крутильная жесткость дерева; МД – приведенный крутящий момент гидропередачи; Мспр – приведенный момент сопротивления; Р – усилие на штоке (штоках) гидроприводов подъема (опускания) стрелы; r – плечо силы Р; Gд – сила тяжести дерева
Далее
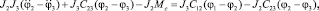
или преобразуя,
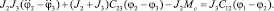(3)
Выразим из уравнения (2) (1 – 2) и 
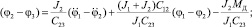
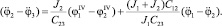
Подставим значения для (2 – 3) и 
в уравнение (3) и преобразуем
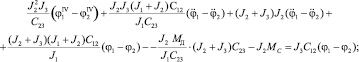
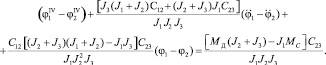
И окончательно
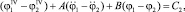(4)
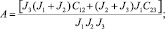
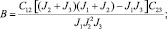
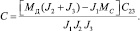
Вводя новую переменную
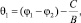
получим однородное уравнение вида
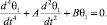(5)
Его характеристическое уравнение имеет вид
(6)
Решение уравнения (5) запишется как
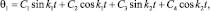(7)
где
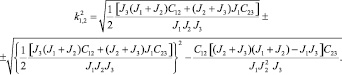
Пример. Принимаем исходные данные применительно к ВПМ ЛП-19А
L=5м; V=2,0м3; hТ=12м; J1=4,05кгм2;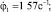 
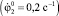C12=30,7Нм; 
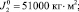J2=0,083кгм2; 
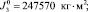J3=0,402кгм2; C23=1,825Нм;
Рассмотрим режимы работы при подъеме дерева стрелой.
1.Определяем коэффициенты дифференциального уравнения (4)
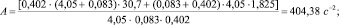
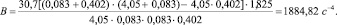
2.Найдем частоты колебаний нагрузки
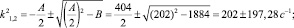
k1=19,92c–1;k2=2,17c–1.
3.Определяем постоянные интегрирования С1…С4.
В соответствии с режимом работы принимаем начальные условия:
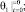
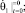
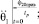
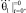
При этих начальных условиях выражения для определения постоянных будут: С1=С3=0;
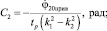
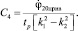
Примем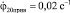 
и tp=0,15c.
Тогда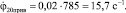 
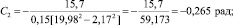
C4=0,265рад.
4.Определяем максимальную динамическую нагрузку на силовую установку ВПМ:
–деформацию упругой связи С12
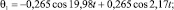θ1max=0,529рад;
–динамический добавочный момент, приведенный к коленчатому валу
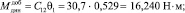
–статический момент, приведенный к коленчатому валу
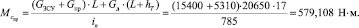
Отбираемая мощность от силовой установки на привод гидронасоса
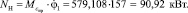
Снижение частоты вращения коленчатого вала
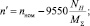N:=10; t:=0,0001...N; n:=0...N;
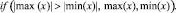
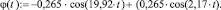
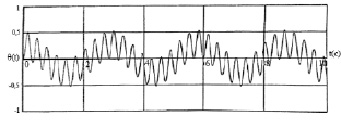
Рис. 2. График изменения деформации упругой связи С12 при разгоне системы (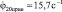
, tp=0,15c)
В случае аварийного торможения системы начальные условия будут
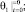
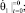
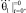
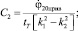
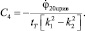
То есть
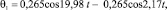
где nном – номинальная частота вращения коленчатого вала; MΣ – суммарный момент.
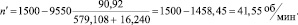
Здесь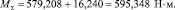
Режим аварийного торможения стрелы манипулятора при подъеме (опускании) горизонтально расположенного дерева сопровождается добавочной динамической нагрузкой на машину. Невысокие значения коэффициентов динамичности определяются большим статистическим моментом в этом случае. При этом снижение частоты вращения коленчатого вала двигателя происходит в пределах допустимых значений.
Разработанная математическая модель динамической системы позволяет с погрешностью 8–10 % определить уровень воздействия на силовую установку в режимах разгона или торможения при освобождении основания деревьев от снега, на этапе разработки конструкторской документации.