Энкодеры (датчики угла поворота) находят широкое применение в устройствах для автоматизированного измерения углов, металлорежущих станках с программным управлением, в роботах и манипуляторах. От точности функционирования энкодеров во многом зависят технические возможности указанных систем. Фотоэлектрические энкодеры, являющиеся в настоящее время наиболее точными, имеют погрешность функционирования в пределах 1–5″, что в ряде случаев недостаточно [4, 5]. Повышение точности возможно, в частности, за счет применения различных методов компенсации погрешностей энкодеров. Вэтом случае необходимо предварительное исследование энкодера для получения информации о суммарной погрешности, анализ которой позволит определить структуру суммарной погрешности (систематическую и случайную составляющие) и степень влияния различных первичных погрешностей энкодера.
Суммарную погрешность энкодера можно описать функцией f(xi), значения которой в i-й точке диапазона [0; 2π) равны y∑i. Всвою очередь y∑i определяется суммой систематической yci и случайной yvi составляющих
f(xi)=y∑i=yci+yvi. (1)
В литературе [3, 6–9] описаны способы, позволяющие получить количественные оценки составляющих суммарной погрешности. Все их можно разбить на две большие группы: прямые и косвенные.
К прямым методам относятся полиноминальная аппроксимация по методу наименьших квадратов, метод скользящей средней, групповой метод, разностный метод, метод «скользящего сглаживания», метод «скользящего суммирования» ординат исследуемой кривой с ординатами её «зеркального отображения», а к косвенным методам – метод построения модуля вектора, метод «бега» фазы, метод построения годографа вектора. Анализ этих методов дан в [6, 7].
Экспериментальные исследования, как правило, дают лишь численные значения суммарной погрешности, поэтому всегда необходим выбор и использование математических средств последующей обработки с целью определения её составляющих.
Анализ прямых методов показал, что:
а)первые 4метода разработаны для случая применения линейных полиномов вида
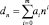 или dn=d0+a1n, (2)
или dn=d0+a1n, (2)
где ai, a0, a1 – коэффициенты; m – порядок полинома, при этом полагается dn=yci, a
yvi=y∑i – yci, (3)
идля другого характера изменения yci не применимы вследствие получения существенных ошибок в определении yci;
б)при использовании следующих методов 5, 6 возможны потери характерных деталей структуры yci при неоднократном применении осреднения;
в)применение однократного осреднения дает грубые оценки составляющих;
г)методы могут использоваться лишь для предварительной оценки составляющих погрешности.
При использовании косвенных методов для выбора пробных периодов необходима исходная информация о характере периодических слагаемых, сумма которых описывает систематическую составляющую yci погрешности. Точность же выделения слагаемых зависит от их количества. Чем больше их содержится в исследуемой суммарной погрешности y∑i, тем грубее значения выделенной систематической составляющей. Это связано с тем, что процесс определения слагаемых ci носит итерационный характер. Погрешности определения параметров, главным образом начальной фазы, найденного слагаемого из первого цикла переходят во второй и т.д., накапливаются, искажая значения параметров последующих выявляемых систематических составляющих.
Поэтому эти методы наиболее эффективны для определения систематических погрешностей, имеющих не более 2–3слагаемых, тогда относительная погрешность определения систематической составляющей суммарной погрешности может быть доведена до величины, равной 10 %. Указанная оценка точности одного из методов получена в результате численного эксперимента на компьютере.
Из изложенного следует, что рассмотренные методы анализа структурного состава суммарной погрешности y∑i в любом случае дают возможность лишь грубого разделения y∑i на систематическую и случайную составляющие, что подтверждает сделанный ранее вывод о необходимости совершенствования этих методов в смысле повышения точности разделения погрешности и адаптации к анализу суммарных погрешностей приборов.
Разработка более точных методов разделения суммарной погрешности опирается на использование в методе1 тригонометрической многочленной аппроксимации.
Тригонометрический многочлен вида
yci=A1sin(x1+ψ1)+...+Аmsin(xm+ψm), (4)
где A1, A2, …, Am – амплитуды; x1, x2, …, xm – периоды; ψ1, ψ2, …, ψm – фазы гармоник, выбран на основе точностного анализа энкодеров, проведенных в [5].
Слагаемые тригонометрического многочлена (гармоники) могут определяться при помощи гармонического анализа, входящего в пакет прикладных программ для персонального компьютера или в среде программного комплекса MAHTCAD. Эти программы гармонического анализа предназначены для анализа y∑i, определенной в диапазоне [0; 2π) числом 2i (i – целое число), либо составлять нечетное число.
При экспериментальном исследовании точности энкодера, которое проводится при метрологической аттестации готового изделия, а также при определении возможности увеличения его точности, получают ограниченный ряд значений y∑i в контролируемых точках диапазона [0; 2π). Аппроксимация полученных значений y∑i рядом Фурье [7, 9] позволяет выявить составляющую yci и найти yvi из выражения (3).
Найденный спектр гармоник yci дает возможность выявить:
–источники первичных погрешностей, а именно, детали и узлы энкодера в соответствии с величинами периодов гармоник в выражении (4);
–степень влияния выявленных источников, которая пропорциональна амплитудам гармоник.
На основе полученной информации об источниках возможно успешное решение вопросов по компенсации наиболее сильно влияющих первичных погрешностей. Реализацию аппроксимации y∑i удобно выполнить с помощью модифицированной подпрограммы «FORIT», которая содержится в библиотеке стандартных программ на ФОРТРАНЕ.
Для получения модифицированного гармонического анализа использован рекуррентный метод, основные положения которого для случая, когда имеется нечетное число точек y∑i на интервале [0; 2π], изложены в [6].
Примем, что функция f(xi), заданная четным числом точек y∑i, равным n=2(2m+2), удовлетворяет условиям Дирихле. Тогда можно записать тригонометрический многочлен вида
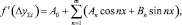 (5)
(5)
где n=1, 2, …, 2m, m – некоторое чётное число; A0, An, Bn – коэффициенты, причём f′(y∑i) наилучшим образом аппроксимирует функцию f(xi),
Обозначим 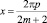 , тогда
, тогда
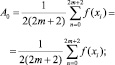 (6)
(6)
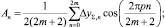 (7)
(7)
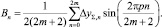 (8)
(8)
Вычисление гармоник в выражении (5) сводится к вычислению коэффициентов An, Bnи A0.
Для вычисления An и Bn используем рекуррентные формулы, полагая p=0, 1, 2,…, m, т.е.
υ2m+3,p=υ2m+2,p=0; (9)
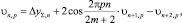 (10)
(10)
при n=2(2m+2); 2(2m+2) – 1, …, 1.
Подставим выражения (9) и (10) в формулы (7) и (8), и можно записать, что
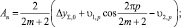 (11)
(11)
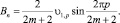 (12)
(12)
При изменении значения n, рекуррентно переходя по формулам (9)–(12), имеем
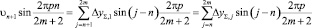 (13)
(13)
и
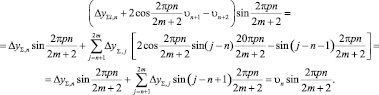 (14)
(14)
Нетрудно заметить, что коэффициенты An и Bn определяются каждый раз при подстановке (13) и (14) в выражение (11) и (12) при j=1, …, 2m.
Выражение (5) можно преобразовать к более компактному виду:
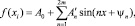 (15)
(15)
где 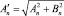 – амплитуда гармоники,
– амплитуда гармоники, 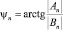 – начальная фаза гармоники.
– начальная фаза гармоники.
Знак фазы ψn выбирается из анализа знаков An и Bn.
Эта подпрограмма вычисляет заданное количество членов ряда (16), не превышающее числа п. Максимальный порядок гармоник п определяется количеством имеющихся значений y∑i, причем выполняется соотношение
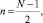 (16)
(16)
где N – число анализируемых точек.
При использовании подпрограммы наибольшая точность достигается при N, равном любому нечетному числу y∑i.
Основным недостатком, который мешает широкому использованию указанной подпрограммы, является зависимость точности разложения от равенства N=k, где k – количество контролируемых значений y∑i, в интервале [0, 2π), получаемое непосредственно при измерениях. Современные высокоточные средства контроля энкодеров не обеспечивают этого равенства, например, наиболее распространенный метод контроля — метод сравнения с образцовой многогранной призмой [4] позволяет получить ограниченное количество k значений y∑i равное числу граней призмы, которое, для случая кодового энкодера, не превышает32. Кроме того, при этом методе не выполняется условие достоверного разложения в ряд (4), имеющее вид т=п при m>15. Однако в энкодерах, особенно накапливающего типа, следует ожидать наличия короткопериодических составляющих погрешности [5]. Этот недостаток можно обойти за счёт увеличения количества анализируемых точек N путём проведения дополнительных измерений y∑i в окрестностях в каждой из k точек и с помощью методов интерполяции увеличить k до N. Применение известных алгоритмов интерполяции на основе методов Ньютона, Гаусса, Бесселя и некоторых комбинированных алгоритмов, в основе которых лежит линейная интерполяция, не позволяет получить высокой точности из-за плохой сходимости ряда (4) и получения полиномов высокой степени. Всвязи с этим разработан алгоритм интерполяции с использованием кубических сплайн-функций [10], подробное изложение теории которых приведено в [1]. Отметим лишь условия, которым должна удовлетворять интерполируемая функция f(xi):
–функция должна быть непрерывна на всем интервале [0, 2π) с аргументами [x1, xk].
–первая и вторая производные f(xi) и f″(xi) непрерывны на [x1, xk].
–вторые производные в конечных точках равны нулю
f″(x1)=f″(xk)=0.
В работе [1] показано, что такая функция, обладающая свойством наименьшей кривизны, является единственной.
Известно, что кубическая сплайн-функция состоит из (k – 1) отрезков кубических кривых, каждый из которых имеет четыре параметра и, следовательно, чтобы однозначно определить кубический сплайн, необходимо вычислить 4(k – 1) параметра. Используя отмеченные ниже условия и учитывая требование f(xi)=y∑i для i=1, ..., k, можно получить систему из 4(k – 1) уравнений с 4(k – 1) неизвестными, которая имеет единственное решение. Учет спектрального состава функции f(xi) и оценка соотношения максимальной гармоники спектра и величины ε-окрестности узлов интерполяции для данной реализации позволяет ввести следующие соотношения:
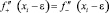
и
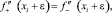
из которых видно, что происходит снижение неопределенности исследуемой функции внутри интервалов интерполяции (xi, xi+1). При выборе двух дополнительных точек внутри интервалов (xi, xi+1), как показали проведённые контрольные просчеты, уже дают приемлемые результаты.
Анализ процесса, который описывается последовательностью y∑i в ε-окрестности, позволил считать его стационарным, поэтому предложенный прием позволяет получить дополнительное число значений y∑i cинтервалом (xi, xi+1), чтобы выдержать соотношение (4) и m=n при N=k+N′, где N′ – число значений y∑i, полученное за счет применения сплайн-интерполяции. Теперь становится возможным использование модифицированной подпрограммы «FORIT» без потери точности разложения и получение полного спектра гармоник суммарной погрешности энкодера.
Предложенный способ был реализован с использованием методики вычисления сплайна, изложенной в [10], и подпрограммы «FORIT» и также отлажен пакет программ анализа точности энкодеров.
Применение разработанной методики для анализа точности фотоэлектрических энкодеров комбинированного типа проводилось на основе исследования y∑i партии из 70энкодеров, изготовленных на одном предприятии. Исследованные энкодеры имели следующие параметры:
–диапазон измеряемых углов [0, 2π);
–дискретность отсчета 1,24″;
–допускаемая суммарная погрешность (по паспорту) 4,4″;
–двоичный последовательный код на выходе.
Измерялась y∑i в N=32 точках диапазона, т.е. дискретность измерения составляла 11,25°.
Было получено выражение для yci в виде
yci=0,65″sin″(x+4,83)+0,60″sin(2x+1,26)+ +0,79″sin(4x+4,67)+0,22″sin(9x – 1,53)+ + 0,42″sin(20x+1,34),
из которого видно наличие гармоники, имеющей угловой период изменения Т20≅18°, являющейся результатом погрешности положения считывающих окон индикаторного лимба, расположенных через 18°.



