Теория краевых задач для вырождающихся гиперболических и смешанного типов уравнений, в силу теоретической и прикладной важности, является одним из интенсивно развивающихся разделов современной теории дифференциальных уравнений с частными производными и привлекает к себе внимание многих исследователей, интересующихся как самой теорией, так и ее приложениями. Локальные и нелокальные задачи для таких уравнений встречаются в теории распространения электромагнитных полей, в теории тепло- и массообмена в средах, окруженных пористой средой, в теории бесконечно малых изгибаний поверхностей, а также в теории оболочек с кривизной переменного знака. Всвязи с изложенным возникает необходимость дальнейшего развития теории нелокальных задач для уравнений смешанного типа. Актуальность этих исследований можно также обосновать внутренними потребностями теоретического обобщения классических задач для уравнений математической физики, получением новых результатов в теории дробного интегро-дифференцирования, а также их прикладным значением.
Для вырождающихся гиперболических и смешанного типов уравнений многими авторами [1–5, 7, 8, 10] исследовались задачи со смещением и задачи типа задачи Бицадзе – Самарского, когда на эллиптической части границы области задано локальное условие, а на характеристической части границы нелокальное условие, поточечно связывающее значения искомого решения или производной от него, вообще говоря, дробной определенного порядка, зависящего от порядка вырождения уравнения.
Цель исследования изучение влияния параметров уравнения и порядков операторов дробного интегро-дифференцирования в краевом условии на однозначную или неоднозначную разрешимость задачи.
Постановка задачи
Рассмотрим уравнение
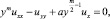(1)
где m≥2, a≠0 – вещественная постоянная, в конечной области Ω, ограниченной характеристиками уравнения (1):
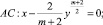
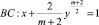
и отрезком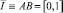 
прямой y=0.
Задача. Найти регулярное в области Ω решение u(x, y) уравнения (1) из класса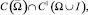 
удовлетворяющее краевым условиям
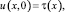
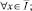(2)
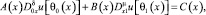
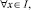(3)
где δ, μ – вещественные числа, A(x), B(x), C(x),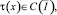 
причем
A2(x)+B2(x)≠0;
θ0(x), θ1(x) – точки пересечения характеристик уравнения (1), выходящих из точки (x, 0)∈I cхарактеристиками AC, BC соответственно;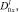 
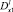– операторы дробного в смысле Римана – Лиувилля интегро-дифференцирования [9, 10].
Разрешимость задачи (2), (3) для обобщенного уравнения Трикоми
ymuxx – uyy=0; m=const>0
при любых δ, μ была исследована И.Оразовым [6].
При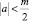 
решение задачи Коши u(x,0)=τ(x), uy(x,0)=ν(x) для уравнения (1) имеет вид [1]
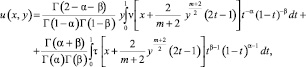(4)
где Γ(z) – гамма функция Эйлера [9].
Пользуясь решением (4), вычислим
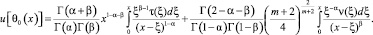
Последнее в терминах операторов дробного интегро-дифференцирования [17] примет вид
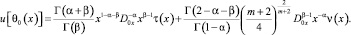
Аналогично получаем
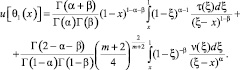
В терминах операторов дробного интегро-дифференцирования последнее примет вид
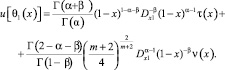
Удовлетворим u[θ0(x)], u[θ1(x)] краевому условию (3). Врезультате преобразований получим
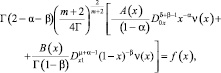(5)
где
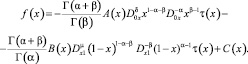
Исследуем разрешимость задачи (1)–(3) для любых промежутков изменения параметров δ, μ.
Теорема 1. Пусть μ=1 – α; δ<1 – α – β; B(x)≠0,
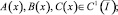
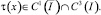
Тогда решение задачи (1)–(3) существует и единственно.
В самом деле, при δ<1 – β и выполнении условий теоремы уравнение (5) примет вид
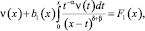(6)
где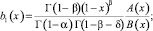 
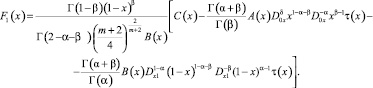
Уравнение (6) есть интегральное уравнение Вольтерра второго рода относительно ν(x) со слабой особенностью в ядре, единственное решение которого в искомом классе функций может быть построено методом последовательных приближений.
Далее, регулярным решением уравнения (1) в области Ω назовем любую функцию u(x, y) из класса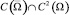 
, удовлетворяющую уравнению (1) в области Ω и такую, что функция uy(x, 0)=ν(x)=xδ+α+β–2ν1(x) в точке x=0 обращается в нуль порядка δ+α+β – 2, а ν1(x) – достаточное число раз дифференцируемая функция в некоторой окрестности (0,δ) точки x=0 и ν1(0)≠0.
Теорема 2. Пусть выполнены условия
μ=1 – α; (1 – β)+k<δ<(1 – β)+k+1, k=1, 2, 3,… .
τ(x)=xσ τ1(x),
где σ≥δ;
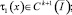
B(x)=x(1 –x)2–αB1(x),
где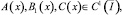 
причем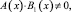 
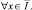Тогда задача (1)–(3) имеет бесконечное множество линейно-независимых решений.
Доказательство. Покажем сначала, что утверждение имеет место при k=1. Вэтом случае уравнение (5) примет вид
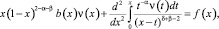(7)
где
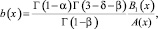
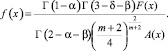
Для доказательства неединственности решения задачи достаточно показать, что соответствующее (7) однородное уравнение
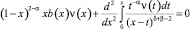(8)
имеет нетривиальное решение.
В самом деле, обозначим
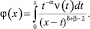(9)
Тогда применяя формулу обращения интегрального уравнения Абеля, получим
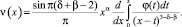
Уравнение (8) примет вид
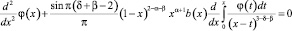. (10)
Полагая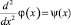 
, после преобразований получим интегральное уравнение
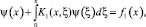(11)
где
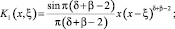
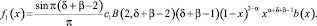
Так как при k=1 по условию теоремы 2 – β<δ<3 – β, то (11) есть интегральное уравнение Вольтерра с непрерывным ядром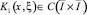 
и непрерывной правой частью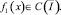 
Уравнение (11) имеет на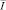 
единственное непрерывное решение
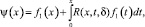
где R(x, t, δ) – резольвента ядра K1(x, t). Тем самым неединственность решения задачи при k=1 доказана. Докажем существование решения задачи.
С учетом (9) уравнение (7), принимая во внимание ранее проведенные вычисления, перепишем в виде
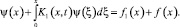(12)
где K1(x, t) и правая часть (12) достаточно гладкие функции.
Известно, что в классе непрерывных функций на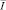 
уравнение (12) имеет непрерывное решение
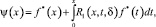
где f*(x)=f1(x)+f(x), а R1(x, t, δ) – резольвента ядра K1(x, ξ).
Допустим, что задача (1)–(3) имеет бесчисленное множество линейно-независимых регулярных решений при k=n – 1, и докажем, что это утверждение верно при i=n.
При k=n; (1 – β)+n<δ<(1 – β)+n+1 и уравнение (7) примет вид
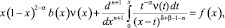(13)
где
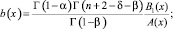
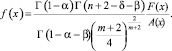
Вводя обозначение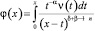 
, а затем 
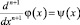, как и ранее при f(x)=0, получим интегральное уравнение Вольтерра второго рода с непрерывным ядром и правой частью
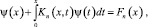(14)
где
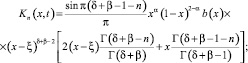
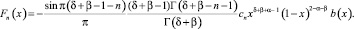
Отсюда следует, что уравнение (14) в классе функций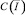 
имеет непрерывное нетривиальное решение, которое задается формулой
,
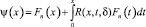и решение задачи (1)–(3) неединственно.
В неоднородном случае получим уравнение
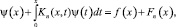
которое имеет непрерывное решение
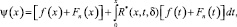
где R*(x, t, δ) резольвента ядра Kn(x, t).
Итак, решение задачи (1)–(3) при выполнении условий теоремы2 существует, но оно неединственно.