Как отмечает А.Ю. Бокин [3], по мнению ряда ведущих специалистов, В.Л. Ботяева, З. Витковски, А.С. Жукова, Н.Л. Журавина, Л.П. Матвеева, А.М. Пидоря и других, наибольшее значение в подготовке квалифицированных спортсменов имеет развитие тех физических качеств в структуре специальной физической подготовки, которые влияют на техническую сторону выполнения соревновательного упражнения и сам спортивный результат. В их исследованиях установлено, что с ростом спортивной квалификации точность выполнения упражнений, их быстрота, прочность овладения двигательными навыками все теснее коррелируют с уровнем спортивных результатов.
Единоборства требуют от спортсмена кроме хорошей физической подготовленности еще и быстроты реакции, высокой скорости принятия решений, устойчивости внимания, высокого уровня функциональных возможностей нервной системы [12]. При этом точность движений, по мнению К.В. Курносова [6], приобретает все большое значение, что в значительной мере обусловлено исчерпанием ресурсов повышения эффективности двигательных действий за счет быстроты, силы и выносливости.
Для тестирования быстроты и точности двигательных действий используется большое количество тестов, среди которых выделяются, как считает И.А. Петров [10], сравнение результатов челночного бега 3×10 м и бега на 30 м, теппинг-тест и точность реакции на движущийся объект.
Цель работы – разработка методики оценки быстроты и точности двигательных действий спортсменов-единоборцев.
Методика оценки быстроты и точности двигательных действий
Испытуемому предъявляют на экране видеомонитора окружность, на которой помещена метка 1 и точечный объект 2, движущийся с заданной скоростью по окружности, как показано на рис. 1.
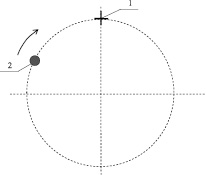
Рис. 1. Схема тестирования реакции на движущийся объект. Обозначения в тексте
Испытуемый, наблюдая за движением точечного объекта 2, в момент предполагаемого совпадения его положения с меткой 1 нажатием кнопки «Стоп» останавливает движение точечного объекта 2 по окружности. Затем вычисляют ошибку несовпадения точечного объекта 2 и метки 1 – время ошибки запаздывания с положительным знаком или упреждения с отрицательным знаком, и через заданное время возобновляют движение точечного объекта 2 по окружности.
Испытуемый выполняет описанную процедуру заданное число раз, после чего строят вариационный ряд ошибок несовпадения точечного объекта 2 и метки 1, вычисляют вариационный размах ряда по формуле
R = tmax – tmin,
где tmax и tmin – соответственно наибольший и наименьший члены вариационного ряда, мс, и отмечают на числовой оси отрезок, ограниченный наибольшим и наименьшим членами вариационного ряда.
Быстроту двигательных действий испытуемого оценивают по расположению на числовой оси отрезка, ограниченного наибольшим и наименьшим членами вариационного ряда ошибок несовпадения точечного объекта и метки, наиболее сдвинутого в область отрицательных значений, точность двигательных действий – по меньшему значению вариационного размаха ошибок несовпадения точечного объекта и метки [8].
Результаты исследования и их обсуждение
В обследовании участвовало по 3 спортсмена 19–22 лет, трех видов единоборств, имеющих первый спортивный разряд, занимающихся дзюдо, рукопашным боем и боксом.
В результате тестирования дзюдоиста В., 20 лет, показавшего лучшие результаты среди дзюдоистов, получены следующие значения ошибок несовпадения положений точечного объекта и метки: – 14, 5, – 22, 18, – 33, – 8, – 43, – 39, 11 и – 31 мс. Наибольший член вариационного ряда ошибок несовпадения точечного объекта и метки равен 18 мс, наименьший член вариационного ряда – минус 43 мс, вариационный размах, вычисленный по формуле – 61 мс. Расположение на числовой оси отрезка, ограниченного наибольшим и наименьшим членами вариационного ряда ошибок несовпадения точечного объекта и метки, представлено на рис. 2, а.

Рис. 2. Расположение на числовой оси результатов тестирования испытуемых
В результате тестирования бойца И., 21 год, показавшего лучшие результаты среди бойцов, получены следующие значения ошибок несовпадения положений точечного объекта и метки: 6, – 13, – 22, – 48, 4, – 13, 1, – 23, – 17 и – 36 мс. Наибольший член вариационного ряда ошибок несовпадения точечного объекта и метки равен 6 мс, наименьший член вариационного ряда – минус 48 мс, вариационный размах, вычисленный по формуле – 54 мс. Расположение на числовой оси отрезка, ограниченного наибольшим и наименьшим членами вариационного ряда ошибок несовпадения точечного объекта и метки, представлено на рис. 2, б.
В результате тестирования боксера М., 19 лет, показавшего лучшие результаты среди боксеров, получены следующие значения ошибок несовпадения положений точечного объекта и метки: 4, – 19, – 33, – 23, – 7, – 38, 9, – 3, – 18 и – 25 мс. Наибольший член вариационного ряда ошибок несовпадения точечного объекта и метки равен 9 мс, наименьший член вариационного ряда – минус 38 мс, вариационный размах, вычисленный по формуле – 47 мс. Расположение на числовой оси отрезка, ограниченного наибольшим и наименьшим членами вариационного ряда ошибок не совпадения точечного объекта и метки представлено на рис. 2, в.
Анализ результатов тестирования свидетельствует, что расположение на числовой оси отрезка, ограниченного наибольшим и наименьшим членами вариационного ряда ошибок несовпадения точечного объекта и метки, наиболее сдвинуто в область отрицательных значений у испытуемого И. (1 разряд по рукопашному бою), следовательно, быстрота его двигательных действий выше, чем у испытуемых В. (1 разряд по дзюдо) и М. (1 разряд по боксу).
Расположение на числовой оси отрезка, ограниченного наибольшим и наименьшим членами вариационного ряда ошибок несовпадения точечного объекта и метки у испытуемого В. (1 разряд по дзюдо) более сдвинуто в область отрицательных значений, чем у испытуемого М. (1 разряд по боксу), следовательно, быстрота его двигательных действий выше.
Вариационный размах ошибок несовпадения точечного объекта и метки у испытуемого М. (1 разряд по боксу) наименьший, следовательно, точность его двигательных действий выше, чем у испытуемых И. (1 разряд по рукопашному бою) и В. (1 разряд по дзюдо).
Вариационный размах ошибок несовпадения точечного объекта и метки у испытуемого И. (1 разряд по рукопашному бою) меньше, чем у испытуемого В. (1 разряд по дзюдо), следовательно, точность его двигательных действий выше.
Аналогичные выводы по быстроте и точности двигательных действий получены при сравнении результатов тестирования дзюдоистов, бойцов и боксеров, показавших худшие результаты среди спортсменов в своем виде спорта.
Современные единоборства требуют от спортсмена быстрого выполнения двигательных и тактических действий в сложных соревновательных ситуациях [1]. Быстрота двигательных действий характеризуется способностью выполнять их в пределах короткого времени. Известны способы оценки быстроты путем определения времени скрытого периода двигательной реакции, скорости одиночного движения, частоты движений в единицу времени и производной от этих показателей – скорости передвижения [4].
Однако эффективность двигательных действий, помимо быстроты, зависит от точности движений, под которой понимают качество двигательного акта, реализованного с соблюдением заранее установленной системы характеристик [2].
Сложным пространственно-временным рефлексом является реакция на движущийся объект [5], поэтому этот тест может использоваться для оценки быстроты и точности двигательных действий спортсменов-единоборцев.
Задача испытуемого, стремящегося остановить движущийся объект, точно совмещая его с меткой (рис. 1), состоит в нахождении некоторой величины упреждения своих двигательных действий с учетом скорости движения объекта, оставшегося расстояния и скорости своих двигательных действий. Ошибки упреждения в тесте являются показателем преобладания возбудительного процесса, ошибки запаздывания – преобладания процесса торможения. Точные реакции в тесте показывают лица с уравновешенными процессами возбуждения и торможения [7]. Действия испытуемого в тесте соответствуют действиям спортсмена-единоборца, что дает возможность оценить не только соотношение возбуждения и торможения, позволяющее оценить быстроту двигательных действий, но и точность двигательных действий испытуемого.
Для оценки времени реакции на движущийся объект вычисляется среднеарифметическое значение ошибок несовпадения точечного объекта и метки [9]. Однако оценка времени реакции на движущийся объект спортсмена-единоборца, вычисленная как среднеарифметическое значение, не позволяет адекватно оценить точность его двигательных действий. Пусть при тестировании времени реакции на движущийся объект двух испытуемых получены следующие значения ошибок несовпадения положений точечного объекта и метки:
– для первого испытуемого + 10, – 10, + 10, – 10, + 10, – 10, + 10, – 10, + 10, – 10 мс;
– для второго испытуемого + 5, – 5, + 5, – 5, + 5, – 5, + 5, – 5, + 5, – 5 мс.
Среднее арифметические значения ошибок несовпадения положений точечного объекта и метки обоих испытуемых совпадают, но их вариационный размах и рассеяние у второго испытуемого меньше, чем у первого, следовательно, точность двигательных действий второго испытуемого выше.
Для характеристики рассеяния (отклонения) значений ошибок несовпадения положений точечного объекта и метки может использоваться дисперсия или стандартное (среднеквадратичное) отклонение. Однако и дисперсия, и стандартное отклонение служат мерой отклонения ошибок несовпадения положений точечного объекта и метки от их среднего значения. Поэтому ни дисперсия, ни стандартное отклонение не могут служить адекватной оценкой точности двигательных действий испытуемого. Пусть при тестирования времени реакции на движущийся объект трех испытуемых получены следующие значения ошибок несовпадения положений точечного объекта и метки:
– для первого испытуемого + 10, – 10, + 5, – 5, + 10, – 10, + 5, – 5, + 10, – 10 мс;
– для второго испытуемого + 15, – 5, 10, 0, + 15, – 5, 10, 0, + 15, – 5 мс;
– для третьего испытуемого + 5, – 15, 0, – 10, + 5, – 15, 0, – 10, + 5, – 15 мс.
Стандартное отклонение ошибок несовпадения положений точечного объекта и метки испытуемых равно 8,8 мс, вариационный размах – 20 мс. Однако расположение на числовой оси отрезка, ограниченного наибольшим и наименьшим членами вариационного ряда ошибок несовпадения точечного объекта и метки, у первого испытуемого симметрично относительно точки 0 (рис. 3, а), у второго испытуемого сдвинуто в область отрицательных значений (рис. 3, б), у третьего испытуемого – в область положительных значений (рис. 3, в). Это свидетельствует о том, что у первого испытуемого процессы возбуждения и торможения в центральной нервной системе уравновешены, у второго испытуемого преобладают процессы возбуждения, у третьего испытуемого – процессы торможения.

Рис. 3. Расположение на числовой оси результатов тестирования испытуемых
Известно, что в выборках людей, обладающих выраженными скоростными качествами, превалирует, наряду с другими, такая особенность, как преобладание возбуждения над торможением [11]. Следовательно, второй испытуемый быстрее реагирует на различные события, изменяющие ситуацию в единоборстве, и как следствие, быстрее выполняет двигательные действия.
Заключение
Предложена методика оценки быстроты и точности двигательных действий спортсменов-единоборцев путем тестирования реакции на движущийся объект, защищенная патентом на изобретение.
Быстрота двигательных действий оценивается по расположению на числовой оси отрезка, ограниченного наибольшим и наименьшим членами вариационного ряда ошибок несовпадения точечного объекта и метки, наиболее сдвинутого в область отрицательных значений, точность двигательных действий – по меньшему значению вариационного размаха ошибок несовпадения точечного объекта и метки.
Тестирование спортсменов 1 разряда, представителей единоборств (дзюдо, рукопашный бой и бокс) показало, что наибольшая быстрота двигательных действий у бойца, далее по показателю быстроты следуют дзюдоист и боксер.
Наилучшая точность двигательных действий у боксера, далее по показателю точности следуют боец и дзюдоист.



