Актуальность задачи обеспечения высокой эффективности технологических процессов комплексов и систем специального назначения обусловлена повышенными требованиями, предъявляемыми к образцам специальной техники. Повышенные требования к характеристикам техники специального назначения, помимо прочего, связаны с высокой конкуренцией, сложившейся в данной области на межгосударственном уровне.
Цель исследования
Наиболее перспективным направлением совершенствования технологических процессов установок некриогенного воздушного диализа, применяемых в качестве элементов комплексов и систем специального назначения, является интенсификация процесса избирательного мембранного массопереноса, наряду с сохранением его селективности.
Материалы и методы исследования
Влияние акустического излучения на процесс диффузионного переноса массы сквозь полимерную мембрану по своей кинетике близок к влиянию температуры, поэтому теоретические исследования акустического воздействия на процесс целесообразно начинать с достаточно хорошо исследованных термических зависимостей.
Термическая зависимость коэффициента растворимости в общем случае характеризуется сорбционными явлениями и оценивается из условия сорбционного равновесия. При достаточно низких давлениях, когда растворимость газов в мембране невелика, выполняется закон Генри [8]:
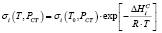, (1)
где σi(T0, PCT) – коэффициент растворимости при условиях, когда экспоненциальный множитель стремится к единице,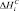 
– энтальпия сорбции газа полимером или энтальпия растворения, определяемая суммой:
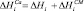, (2)
где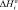 
– энтальпия адсорбции, которая всегда отрицательна, 
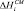– энтальпия смешения при образовании раствора в матрице мембраны.
Зависимость коэффициента диффузии от температуры выражается уравнением активационной теории самодиффузии, для коэффициента самодиффузии:
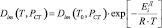, (3)
где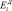 
– энергия активации диффузии для данной системы «полимер-газ», Di(T0, PCT) – коэффициент диффузии при условиях, когда экспоненциальный множитель стремится к единице.
Учитывая, что коэффициент проницаемости Λi = Dim?σi, из (1) и (3) можно получить соотношение, определяющее его зависимость от температуры:
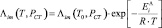, (4)
где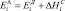 
– так называемая энергия активации проницания для данной системы полимер-газ, Λi(T0, PCT) – постоянная, определяемая по опытным данным и имеющая смысл коэффициента проницаемости при условиях, когда экспоненциальный множитель стремится к единице.
Таким образом, температурная зависимость коэффициента проницаемости мембраны, характеризующего процесс, должна определяться изменением величины энергии активации проницания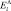 
, по экспоненциальному закону (4).
Результаты исследования и их обсуждение
Влияние ультразвука на проницание газов сквозь полимерную мембрану также целесообразно оценивать по изменению характеристик проницаемости мембраны по компонентам смеси в зависимости от мощности, вносимой в процесс акустической энергии.
В общем случае, проницание газа сквозь гомогенную мембрану рассматривается как процесс переноса массы диффундирующего газа, растворенного в неподвижном веществе мембранной матрицы. Это характеризуется парциальным коэффициентом самодиффузии D0im, который в идеальных условиях равен коэффициенту диффузии [1].
Согласно гидродинамической теории коэффициент диффузии отражает тепловую подвижность bim частиц диффундирующего вещества в растворе, определяемую уравнением (5) Стокса – Эйнштейна:
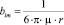, (5)
где r – радиус сферической частицы, мигрирующей в среде с вязкостью μ, и связан с ней термодинамическим коэффициентом Больцмана kБ:
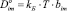, (6)
где T – внутренняя температура. На значение температуры в рамках данной модели может оказывать влияние количество внешней энергии, вносимой в систему акустической волной, в сторону ее увеличения [2, 3], увеличивая, таким образом, парциальный коэффициент самодиффузии.
Большой интерес с точки зрения оценки акустического воздействия на процесс представляет активационная теория самодиффузии в плотных кристаллических и аморфных средах. Данная теория основывается на положении, что в структуре матрицы вследствие теплового движения происходит непрерывное перераспределение межмолекулярных пустот (вакансий). Движение вакансий эквивалентно миграции частиц. Перенос массы возможен при одновременном соблюдении двух условий: возникновение вакансии и достижение достаточно большой энергии колебаний частицы около положения равновесия [5]. Оба этих условия подразумевают энергетические предпосылки. Таким образом, циклическое внесение внешней энергии в систему, например, при помощи звуковой волны, может послужить своеобразным синхронизирующим фактором, увеличивающим вероятность их совпадения.
В рамках данной теории коэффициент самодиффузии пропорционален смещению <l> и средней скорости частиц <u>:
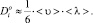(7)
Определяя среднюю скорость по длительности периода <t> «оседлой жизни» частицы в положении равновесия:
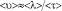, (8)
отсюда
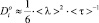, (9)
где <t>-1 – так называемая частота перескока, пропорциональная произведению вероятностей двух одновременных событий: появления вакансии (~A1×exp[– e1/kБ×T]) и достижения частицей энергии для перехода в новое положение равновесия (~A2×exp[– e2/kБ×T]).
Таким образом, коэффициент самодиффузии можно представить в виде
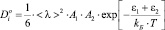, (10)
где e1, A1 – энергия активации и коэффициент вероятности появления вакансии; e2, A2 – энергия активации и коэффициент вероятности достижения частицей энергии перехода.
Чтобы описать воздействие ультразвуковой волны на процесс диффузии необходимо учесть акустическую энергию Еw поглощенную системой, которая согласно закону сохранения энергии равна
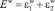, (11)
где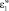 
– акустическая энергия, поглощенная матрицей мембраны; 
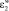– акустическая энергия, поглощенная диффундирующим газом, растворенным в веществе мембраны. Соотношение слагаемых зависит от растворимости компонентов, которая также повлияет на эффект ультразвука, оказываемый процесс, хотя очевидно, что 
.
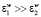Практическая ценность уравнения (12) заключается в обосновании вида температурной зависимости коэффициентов самодиффузии:
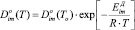, (12)
где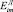 
– энергия активации диффузии растворенного газа; 
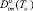– постоянная для данной диффузионной среды, определяемая опытным путем.
Энергия активации диффузии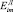 
является функцией свойств диффузанта и среды, положительна и обычно возрастает с увеличением размеров молекулы и параметров межмолекулярного потенциала eii* и sii* [1]. Соотношения для расчета 
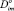и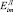 
через молекулярные характеристики диффузанта и свойства полимерной матрицы приведены во многих теоретических работах [7].
Для обоснования закономерностей диффузии в полимерных мембранах большое распространение получила концепция свободного объема, согласно которой процесс миграции не является активационным. Смещение частицы в определенном направлении полностью определяется вероятностью возникновения микрополости с объемом, превышающим некоторое критическое значение.
Относительно акустического воздействия, по аналогии с механизмом направленной диффузии в кавитационных процессах [6], можно выдвинуть предположение, что звуковая волна, представляющая собой чередование областей сжатия и разряжения вещества, способна оказать влияние на процесс образования микрополостей в веществе мембраны. Очевидно, что в рамках теории свободного объема данный процесс будет описываться совместной вероятностью, образования свободных объемов, превысивших критическое значение в области разряжения матрицы мембраны, под воздействием звуковой волны.
Рассматривая вероятность образования объема, превышающего критическое значение, как экспоненциальную функцию отношения критического (Vi*) и свободного (Vf) объемов в полимере, подвижность частиц можно представить в виде
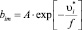, (13)
где A – коэффициент вероятности образования объема больше критического; ui* – относительный критический объем, f – относительный свободный объем
; 
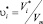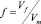, (14)
где Vm – удельный объем диффузионной среды. Тогда коэффициент самодиффузии согласно (6)
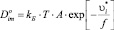. (15)
В этом уравнении аргумент экспоненты несет всю информацию о составе диффузанта и матрицы мембраны, влиянии температуры и давления на скорость миграции частиц.
Для расчета и анализа удобнее исключить коэффициент вероятности, используя опорное состояние диффузионной среды, в качестве которого в полимерных мембранах чаще всего используют состояние полимерной матрицы при температуре стеклования [7, 4]:
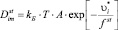, (16)
где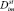 
– коэффициент самодиффузии мембраны из данного материала при температуре стеклования полимера; fst – относительный свободный объем матрицы мембраны при температуре стеклования.
Тогда выражение, связывающее коэффициент самодиффузии с долей свободного объема f при различных значениях температуры, давления и состава раствора, примет вид
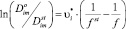. (17)
Таким образом, основные модельные теории самодиффузии газов в конденсированной фазе, рассмотренные выше, не исключают наличия положительного эффекта от стимулирующего акустического воздействия. А рассмотренные вероятностные модели (активационная и концепция свободных объемов) выглядят наиболее удобными для описания воздействия ультразвуковой волны на процесс диффузии газов в полимерной мембране.
Согласно положениям активационной теории акустическая энергия EW, вносимая в систему энергия ультразвука, частично поглощается диффундирующим веществом, растворенным в мембране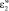 
и самой матрицей мембраны 
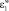, повышая их тепловую активность.
Разумно предположить, что в рамках активационной теории потенциальный энергетический порог преодоления диффундирующей частицей положения равновесия в условиях ультразвукового излучения будет снижен на величину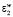 
, подобным образом избыток энергии, затрачиваемой на образование вакансии в матрице, будет равен количеству акустической энергии 
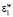, поглощаемой веществом мембраны, таким образом, суммарная энергия активации диффузии EΛW изменится на величину EW:
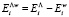, (18)
где могут быть рассмотрены четыре характерных случая акустического воздействия:
I.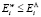 
– интенсификация процесса массопереноса сквозь мембрану.
II.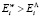 
– стимулирующее действие на процесс массопереноса.
III.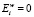 
– толерантность процесса массопереноса к воздействию.
IV.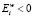 
– ухудшение переноса массы сквозь вещество мембраны.
Очевидно, что количество акустической энергии, вносимой в систему, прямопропорционально интенсивности ультразвукового излучения, воздействующего на процесс. Данным фактом можно воспользоваться для осуществления количественной оценки величины акустической энергии, вносимой в систему:
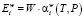, (19)
где W – интенсивность ультразвука, [Вт/м2];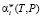 
– коэффициент, характеризующий степень поглощения акустической энергии системой «полимер-газ», [м2×с/моль].
Подставив формулы (18) и (19) в (4), получим уравнение, описывающее влияние ультразвукового излучения на процесс проницания газа сквозь полимерную мембрану:
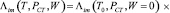
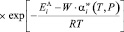, (20)
где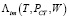 
– коэффициент проницаемости i-го компонента смеси при различной интенсивности ультразвукового излучения, воздействующего на процесс, [моль×м/(м2×с×Па)]; 
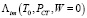– постоянная, определяемая по опытным данным и имеющая смысл коэффициента проницаемости при условиях, когда экспоненциальный множитель стремится к единице, а акустическое воздействие на процесс отсутствует.
Заключение
Таким образом, акустическая зависимость коэффициента проницаемости мембраны, характеризующего процесс, должна определяться изменением величины суммарной энергии активации проницания в условиях ультразвукового излучения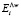 
, по экспоненциальному закону (20), при этом в случае 
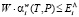имеет место интенсификация процесса.