Ландшафтная архитектура – это «искусство создавать гармоничное сочетание естественного ландшафта с освоенными человеком территориями, населенными пунктами, архитектурными комплексами и сооружениями. В задачи ландшафтной архитектуры входят охрана естественных ландшафтов и …» (Большой Энциклопедический словарь).
Чтобы из искусства перейти к науке, необходимо измерить поведение разных видов, типов и структур сосняков к создаваемым удобрениями лесным почвам. Это позволило бы ускорить выявление закономерностей влияния почвы на древостои. Но и сами древостои, как известно, за десятилетия формируют свои места произрастания.
Поэтому цель статьи – показать методику определения потребности лесной почвы в питательных веществах по типам леса в зависимости от прогнозируемой продуктивности древостоев по запасу стволовой древесины плантационных сосняков.
Для лесных древесных плантаций, то есть специально отведенных лесных земельных участков для прямого вмешательства человека в жизнь лесных деревьев, необходимы устойчивые закономерности влияния параметров древостоя на формирование почвенного покрова и изменение его биохимических компонентов.
По мнению А.К. Каяндера «… действительно биологически родственные типы леса стояли в этой системе, возможно, ближе друг к другу». Однако «… типы леса всегда группировались по их нормальным формам (т.е. по растительным сообществам, представляющим спелые, нормально сомкнутые и развившиеся насаждения)». Таким образом, априори, без всякого количественного доказательства, то есть аксиоматически, предполагалась высокая теснота связи между древостоем и почвой в одном типе леса: «Эти нормальные формы, в свою очередь, группировались таким образом, что все сообщества, имеющие близкий видовой состав растительности и соответственно ближе друг к другу стоящие, объединялись в одну группу». И тут же А.К. Каяндер критикует методологию типизации: «Этой, как и всякой естественной системе, само собой понятно, свойственно очень много субъективного» [5, с. 29].
Любая типизация относится к созерцательному творчеству и, как правило, выполняется по эвристическим признакам. Но, как подчеркивал А.К. Каяндер, на одной и той же почве могут произрастать разные типы леса. Он в своей брошюре привел данные экспериментов других авторов по древостоям и почве по отдельности. В этом его заслуга, хотя сам не сумел и, по-видимому, даже не пытался объединить количественные данные измерений.
Концепция лесопользования. Древопользование, как процесс извлечения из леса древесного сырья, является прямым вмешательством в жизнь леса, вплоть до ее полного прекращения сплошными рубками деревьев. В отличие от сельского хозяйства [1], этот процесс будет происходить десятилетиями, но по обработке почвы станет частью растениеводства. В истинном смысле слова заготовка – это лесной земельный участок, на котором проводится растениеводство с активным и интенсивным удобрением почвы для достижения прогнозной продуктивности по объему кругляка при достижении технической (финансовой) спелости стволов.
Таким образом, сплошные рубки должны уйти в плантационное древопользование.
Исходные данные. Совмещенные данные (табл. 1) измерений J. Ilvessalo из книги [5] позволили нам выявить биотехнические закономерности влияния древостев на почву.
Таблица 1
Показатели сосняков разного возраста и лесной почвы по пяти типам леса
|
Тип леса |
Запас V в возрасте A нормального сосняка, м3/га |
На 1 аре |
На 1 га, кг |
|||||||||||||||
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
прок, |
электр, |
N |
P2O5 |
K2O |
CaO |
|
|
OMT |
19 |
70 |
140 |
208 |
279 |
344 |
405 |
458 |
500 |
535 |
560 |
576 |
1,448 |
794 |
3,315 |
0,492 |
486 |
1,478 |
|
MT |
13 |
60 |
135 |
200 |
260 |
313 |
363 |
407 |
443 |
472 |
492 |
503 |
1,237 |
497 |
2,428 |
0,910 |
446 |
1,257 |
|
VT |
10 |
44 |
87 |
134 |
177 |
219 |
262 |
299 |
328 |
351 |
366 |
375 |
1,029 |
271 |
1,726 |
1,479 |
449 |
0,996 |
|
CT |
7 |
24 |
47 |
75 |
104 |
128 |
153 |
178 |
203 |
222 |
240 |
254 |
1,085 |
418 |
1,547 |
1,080 |
429 |
0,680 |
|
CIT |
– |
3 |
10 |
17 |
31 |
46 |
62 |
80 |
98 |
114 |
132 |
148 |
0,601 |
220 |
0,860 |
1,471 |
531 |
0,464 |
Первичные данные по 240 модельным соснам и пробным площадям, а также более 600 почвенным пробам, можно бы поместить в общую таблицу для моделирования.
Влияние запаса на почву. По табл. 2 коэффициент функциональной связности (коррелятивной вариации) равен 0,975. Этот показатель очень высокий и показывает тесную взаимную связь между учтенными финнами в экспериментах факторами.
Таблица 2
Влияние древостоев на почву
|
A, лет |
Коэффициент корреляции по веществам |
Ix |
||||||
|
прок. |
элек. |
N |
P2O5 |
K2O |
CaO |
Σ |
||
|
10 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
0,9998 |
5,9998 |
1 |
|
20 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
0,9710 |
0,9995 |
5,9705 |
2 |
|
30 |
1,0000 |
1,0000 |
0,9971 |
0,9159 |
0,9331 |
0,9876 |
5,8337 |
6 |
|
40 |
1,0000 |
0,9999 |
0,9965 |
0,9138 |
0,9367 |
0,9887 |
5,8356 |
5 |
|
50 |
1,0000 |
0,9923 |
1,0000 |
0,9191 |
0,9431 |
0,9930 |
5,8475 |
3 |
|
60 |
1,0000 |
0,9825 |
0,9989 |
0,9152 |
0,9476 |
0,9961 |
5,8403 |
4 |
|
70 |
1,0000 |
0,9762 |
0,9974 |
0,9110 |
0,9509 |
0,9979 |
5,8334 |
7 |
|
80 |
1,0000 |
0,9715 |
0,9963 |
0,9082 |
0,9513 |
0,9986 |
5,8259 |
8 |
|
90 |
1,0000 |
0,9689 |
0,9959 |
0,9072 |
0,9508 |
0,9988 |
5,8216 |
9 |
|
100 |
1,0000 |
0,9660 |
0,9953 |
0,9061 |
0,9490 |
0,9989 |
5,8153 |
10 |
|
110 |
1,0000 |
0,9629 |
0,9949 |
0,9056 |
0,9460 |
0,9988 |
5,8082 |
11 |
|
120 |
1,0000 |
0,9598 |
0,9945 |
0,9047 |
0,9433 |
0,9987 |
5,8010 |
12 |
|
Σ |
12 |
11,780 |
11,967 |
11,107 |
11,423 |
11,957 |
70,233 |
– |
|
Ix |
1 |
4 |
3 |
6 |
5 |
2 |
– |
0,975 |
Наибольшую общую тесноту связи, как влияющая переменная, получили сосняки в возрасте 10 лет, то есть молодняки оказывают на концентрацию химических веществ в лесной почве наибольшее влияние.
Почти однозначную зависимость получили потери от прокаливания (этот показатель косвенно дает сумму веществ).
На втором месте как показатель находится кальций, а на третьем – общий азот.
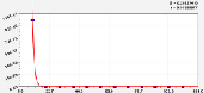
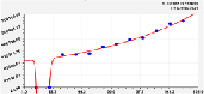
Влияние 10-летних сосняков. На потери от прокаливания почвы и концентрации пяти веществ в лесной почве Южной Финляндии (на 1916–1918 гг.) запас в 10 лет дает влияние (рис. 1) по биотехническим закономерностям:

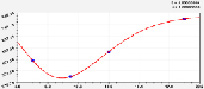
Потери от прокаливания Содержание электролитов
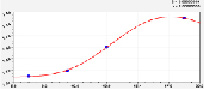
Концентрация азота, кг/га Концентрация фосфора, кг/га
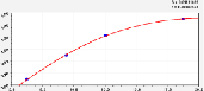
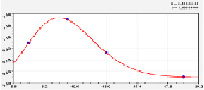
Концентрация калия, кг/га Концентрация кальция, кг/га
Рис. 1. Влияние запаса стволовой древесины на содержание веществ в почве в сосняках 10-летнего возраста
Прок = 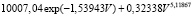 ; (1)
; (1)
Элек = 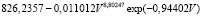 ; (2)
; (2)
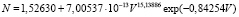 ; (3)
; (3)
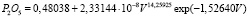 ; (4)
; (4)
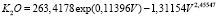 ; (5)
; (5)
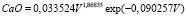 . (6)
. (6)
Задаваясь требуемым к 10-летнему возрасту плантационного сосняка объемом стволовой древесины, по формулам можно вычислить потребное количество видов удобрения.
Например, при условии V = 0, то есть за 10 лет на земельном участке нет молодняка древостоя, получаем следующие предельные значения: Прок = 1007; Элек = 826; N = 1,53 кг/га; P2O5 = 0,48 кг/га; K2O = 263,4 и CaO = 0 кг/га.
По графикам прокаливания, электролитов и фосфора на рис. 1 заметно, что запас древостоя четко разделяется на две интервала:
а) от нуля до V1 = 8,2 – 9,4;
б) V > 9,4 м3/га.
По рейтингу веществ (см. табл. 2) рассмотрим динамику первого параметра моделей.
Потери при прокаливании. Общее уравнение изменение показателя (табл. 3):
Таблица 3
Влияние запаса на прокаливание
|
А |
а1 |
а2 |
а3 |
а4 |
а5 |
|
10 |
1007,4 |
– 1,53943 |
0,32338 |
0,51187 |
0 |
|
20 |
0,42871 |
0,017280 |
0,032032 |
1,73004 |
0,12036 |
|
30 |
7,47103e-6 |
0,081766 |
0,14632 |
0,66469 |
0,011816 |
|
40 |
9,50967e-6 |
0,053776 |
0,090806 |
0,71589 |
0,0081435 |
|
50 |
0,0071820 |
0,017542 |
0,017994 |
1,11109 |
0,010597 |
|
60 |
0,060227 |
0,0087352 |
0,0016821 |
1,65960 |
0,013833 |
|
70 |
0,15397 |
0,0053746 |
3,71936e-5 |
2,51026 |
0,017900 |
|
80 |
0,22521 |
0,0040066 |
1,83049e-7 |
3,66378 |
0,022153 |
|
90 |
0,25382 |
0,0034545 |
8,92273e-10 |
4,77635 |
0,025124 |
|
100 |
0,28510 |
0,0030267 |
1,30983e-12 |
6,13469 |
0,028953 |
|
110 |
0,31091 |
0,0027471 |
5,56959e-17 |
8,23863 |
0,035238 |
|
120 |
0,33660 |
0,0025401 |
4,41865e-23 |
11,17978 |
0,044300 |
Прок = 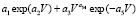 . (7)
. (7)
При условии V = 0, то есть на лесном пустыре (поляне, прогалине), будет уравнение
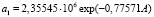 . (8)
. (8)
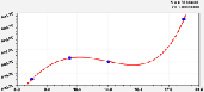
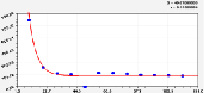
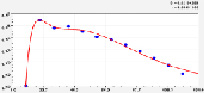
График потерь при прокаливании и других показателей почвы по первому параметру модели (7) приведен на рис. 2. По-видимому, поляны и прогалины возникают из-за несоответствия потребностей деревьев в питании биохимическому потенциалу лесной почвы.
Оксид кальция. Влияние (табл. 4) запаса на кальций имеет вид уравнения
Таблица 4
Влияние запаса на оксид кальция
|
А |
а1 |
а2 |
а3 |
а4 |
а5 |
а6 |
|
10 |
0 |
0 |
1 |
0,03352 |
1,8686 |
0,09026 |
|
20 |
0,42305 |
0,032125 |
0,86189 |
0 |
0 |
0 |
|
30 |
0,37076 |
0,045181 |
0,68403 |
0 |
0 |
0 |
|
40 |
0,38137 |
0,022072 |
0,76395 |
0 |
0 |
0 |
|
50 |
0,35096 |
0,022697 |
0,73218 |
0 |
0 |
0 |
|
60 |
0,31575 |
0,029005 |
0,67775 |
0 |
0 |
0 |
|
70 |
0,29547 |
0,029666 |
0,66343 |
0 |
0 |
0 |
|
80 |
0,26256 |
0,037555 |
0,62368 |
0 |
0 |
0 |
|
90 |
0,22348 |
0,052563 |
0,57540 |
0 |
0 |
0 |
|
100 |
0,17970 |
0,084681 |
0,51090 |
0 |
0 |
0 |
|
110 |
0,13362 |
0,14045 |
0,44824 |
0 |
0 |
0 |
|
120 |
0,077791 |
0,29383 |
0,36230 |
0 |
0 |
0 |
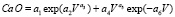 . (9)
. (9)
Первый параметр модели (9) определяется (рис. 2) уравнением
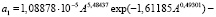
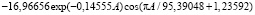 . (10)
. (10)
Потери от прокаливания Содержание электролитов
Концентрация азота, кг/га Концентрация фосфора, кг/га
Концентрация калия, кг/га Концентрация кальция, кг/га
Рис. 2. Динамика содержания веществ в почве в сосняках при условии V = 0
Волновое колебание сильное в период до 50 лет и максимальное при условии А = 0. Для лесной поляны или прогалины оксид кальция становится хорошим индикатором.
Общий азот. Общее уравнение (табл. 5) изменяется по формуле
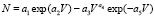 . (11)
. (11)
Таблица 5
Влияние запаса на общий азот
|
А |
а1 |
а2 |
а3 |
а4 |
а5 |
|
10 |
1,52630 |
0 |
– 15,13886 |
0,84254 |
1,52630 |
|
20 |
0,83184 |
0,029324 |
3,56019e-7 |
4,49946 |
0,044606 |
|
30 |
0,57776 |
0,028758 |
6,86019e-7 |
3,55406 |
0 |
|
40 |
0,54989 |
0,019315 |
1,32717e-7 |
3,58615 |
0 |
|
50 |
0,58533 |
0,012893 |
1,48010e-7 |
3,30636 |
0 |
|
60 |
0,58607 |
0,0099440 |
9,81391e-8 |
3,22191 |
0 |
|
70 |
0,57201 |
0,0082800 |
5,56015e-8 |
3,20993 |
0 |
|
80 |
0,54524 |
0,0073218 |
2,76405e-8 |
3,24967 |
0 |
|
90 |
0,50768 |
0,0068236 |
1,18672e-8 |
3,33720 |
0 |
|
100 |
0,48200 |
0,0064435 |
6,13146e-9 |
3,40303 |
0 |
|
110 |
0,44483 |
0,0062804 |
2,56078e-9 |
3,51435 |
0 |
|
120 |
0,41150 |
0,0062107 |
1,12143e-9 |
3,62501 |
0 |
В отличие от формул (7) и (9) вторая составляющая становится кризисной.
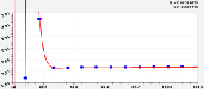
Первый параметр формулы (11) определяется (рис. 2) закономерностью
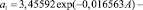
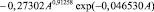 . (12)
. (12)
Сосняки обедняют азот почвы, поэтому до 40 лет им нужны азотные удобрения.
Содержание электролитов. Общее уравнение (табл. 6) аналогично азоту
Элек = 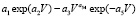 . (13)
. (13)
При этом первый параметр формулы (13) определяется (рис. 2) выражением
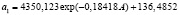 . (14)
. (14)
Таким образом, чтобы было возобновление на пустом от древостоя земельном участке почва должна содержать не менее 4350 + 136 = 4486 электролита. Молодняк до 30 лет быстро использует электролит почвы, а затем сосновый древостой поддерживает на уровне 136,5.
Таблица 6
Влияние запаса на электролиты почвы
|
А |
а1 |
а2 |
а3 |
а4 |
а5 |
|
10 |
826,2367 |
0 |
0,011012 |
8,80247 |
0,94402 |
|
20 |
243,5524 |
0,019249 |
1,79995e-21 |
18,26426 |
0,35410 |
|
30 |
163,3841 |
0,029289 |
0,00051099 |
3,37779 |
0 |
|
40 |
156,1427 |
0,019736 |
0,00010244 |
3,42005 |
0 |
|
50 |
0,016992 |
0,013080 |
0,00019173 |
3,05665 |
0 |
|
60 |
171,1348 |
0,010043 |
0,00017950 |
2,92115 |
0 |
|
70 |
167,5261 |
0,0083685 |
0,00012087 |
2,89040 |
0 |
|
80 |
160,6821 |
0,0073945 |
7,13760e-5 |
2,90970 |
0 |
|
90 |
151,5230 |
0,0068626 |
3,76850e-5 |
2,96871 |
0 |
|
100 |
146,1133 |
0,0064322 |
2,57400e-5 |
2,99231 |
0 |
|
110 |
138,6126 |
0,0061826 |
1,68870e-5 |
3,03127 |
0 |
|
120 |
132,4365 |
0,0060160 |
1,25430e-5 |
3,05644 |
0 |
Оксид калия. Влияние запаса на калий (табл. 7) проявляется по уравнению
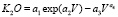 . (15)
. (15)
По сравнению с азотом и электролитом в кризисной части (15) нет торможения.
Таблица 7
Влияние запаса на оксид калия
|
А |
а1 |
а2 |
а3 |
а4 |
|
10 |
263,4178 |
0,11396 |
1,31154 |
2,45547 |
|
20 |
1171,119 |
0,0023890 |
0,057748 |
0,10588 |
|
30 |
112557,5 |
1,33523e-5 |
111821,1 |
0,00085977 |
|
40 |
112594,8 |
9,60619e-6 |
111783,4 |
0,00094541 |
|
50 |
116491,3 |
8,47249e-6 |
115523,5 |
0,0011738 |
|
60 |
137952,9 |
6,81263e-6 |
136835,2 |
0,0012026 |
|
70 |
148657,2 |
6,08888e-6 |
147393,1 |
0,0012970 |
|
80 |
163193,6 |
5,50904e-6 |
161764,7 |
0,0013673 |
|
90 |
169086,6 |
5,35505e-6 |
167493,0 |
0,0014973 |
|
100 |
192983,5 |
4,74826e-6 |
191240,8 |
0,0014514 |
|
110 |
217720,7 |
4,43259e-6 |
215778,3 |
0,0014586 |
|
120 |
227402,1 |
4,52253e-6 |
225255,1 |
0,0015682 |
Первый параметр уравнения (15) изменяется (рис. 2) по двухчленной формуле
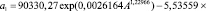
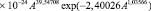 . (16)
. (16)
Сосняк требует калия по закону экспоненциального роста, но в интервале 7–24 лет наблюдается кризисное снижение потребления. По-видимому, здесь должен быть какой-то биохимический эффект кризисной адаптации стрессовым возбуждением растущих сосен.
Оксид фосфора. Общее уравнение (табл. 8) имеет спад первого члена формулы
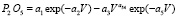 . (17)
. (17)
Таблица 8
Влияние запаса на оксид фосфора
|
А |
а1 |
а2 |
а3 |
а4 |
а5 |
|
10 |
0,48038 |
0 |
– 2,33144e-8 |
14,25925 |
0,15264 |
|
20 |
5,41295 |
0,43454 |
– 1,08328e-5 |
4,53638 |
0,12124 |
|
30 |
1,30667 |
0,00069233 |
4,91714e-27 |
12,23788 |
0 |
|
40 |
1,31017 |
0,00042582 |
3,00202e-26 |
10,98975 |
0 |
|
50 |
1,34635 |
2,88420e-5 |
3,06784e-26 |
10,40353 |
0 |
|
60 |
1,34776 |
3,87010e-5 |
2,13898e-22 |
8,51514 |
0 |
|
70 |
1,34709 |
3,02096e-5 |
5,06869e-21 |
7,75774 |
0 |
|
80 |
1,34926 |
3,61432e-5 |
1,25667e-20 |
7,45345 |
0 |
|
90 |
1,35528 |
5,03340e-5 |
1,45539e-20 |
7,32331 |
0 |
|
100 |
1,36125 |
6,79373e-5 |
1,34632e-20 |
7,25538 |
0 |
|
110 |
1,37174 |
9,54090e-5 |
1,80676e-20 |
7,15416 |
0 |
|
120 |
1,38309 |
0,00012184 |
5,30965e-20 |
6,95067 |
0 |
Первый параметр уравнения (17) изменяется (рис. 2) по формуле с волной:
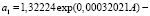
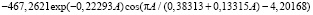 . (18)
. (18)
Сильная флюктуация наблюдается в возрасте сосняка от 0 до 30 лет.
Качество гумуса. Качество гумуса почвы (табл. 9) определяет добротность места произрастания: «Приведенные цифры с несомненностью доказывают, что в более или менее однородной климатической области определенные качества почвы (их средние значения) изменяются параллельно добротности мест произрастания» [5, с. 38].
Таблица 9
Влияние типа леса на гумус
|
Тип леса |
Код R |
Общий азот N, % |
Связанный азот NH4, % |
Кислотность pH |
|
|
проба |
2 мес. |
||||
|
OMaT |
6 |
2,795 |
0,551 |
4,425 |
5,0 |
|
OMT |
5 |
2,234 |
0,484 |
2,868 |
5,2 |
|
MT |
4 |
1,796 |
0,383 |
1,819 |
4,8 |
|
VT |
3 |
1,666 |
0,335 |
1,207 |
4,6 |
|
CT |
2 |
1,495 |
0,220 |
1,074 |
4,2 |
|
CIT |
1 |
– |
– |
– |
3,6 |
Суждение «изменяются параллельно» получено созерцательно (интуитивно) по данным Aaltonen, который арифметически усреднил данные измерений по 800 пробам гумуса.
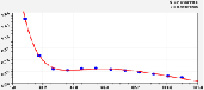
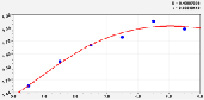
Уравнение (рис. 3) pH имеет вид трехчленной закономерности с биотехническим законом:
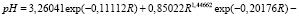
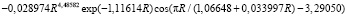 . (19)
. (19)
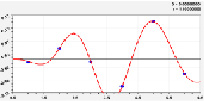
Содержание общего азота характеризуется (рис. 3) уравнением вида
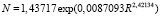 . (20)
. (20)
Водородный показатель гумуса по тренду
Колебательное возмущение водной кислотности
Содержание общего азота в гумусе, %
Доля нитрата в сухом гумусе через 2 месяца, %
Рис. 3. Влияние кода типа леса на показатели качества гумуса лесной почвы
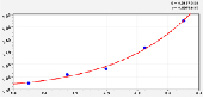
Аналогичную конструкцию экспоненциального закона роста получили уравнения:
– связанный азот сразу же после взятия пробы почвы
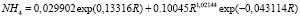 ; (21)
; (21)
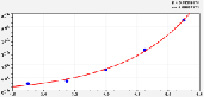
– связанный азот через два месяца после естественной сушки пробы почвы
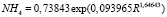 . (22)
. (22)
Заключение
Практически все лесные ландшафты на Земле стали природно-антропогенными комплексами [6, 9, 10]. При этом уровень антропогенности лесного ландшафта вполне можно измерять по резким изменениям в жизни популяций деревьев [2, 8, 10] и снижением качественных свойств их древесины [3, 4, 7]. Поэтому экологические и технологические цели обычно совпадают – это повышение качества.
Между почвой и древостоем наблюдаются явно нелинейные закономерности и колебательные адаптации друг к другу по параметрам. В любой схеме типизации лесов, как редуцировании природных процессов, волна взаимного влияния очень грубо затушевана.
Моделирование данных J. Ilvessalo из книги [5] дало высокоадекватные закономерности. Типы леса не являются устойчивыми факторами – это искусственное изобретение лесоводов для облегчения расчетов.



