Математический аппарат и лежащие в его основе математические методы все активнее проникают во все виды деятельности человека. Знание математических методов перестает быть только средством общего развития и приобретения навыков элементарных расчетов. Математический склад мышления становится необходимым для специалистов всех направлений научной и практической деятельности [8].
Математическую компетенцию будущего выпускника технического вуза исследователи определяют как способность структурировать данные, вычленять математические отношения, создавать математическую модель ситуации, анализировать и преобразовывать ее, интерпретировать полученные результаты [2]. Поэтому математическая компетенция способствует адекватному применению математики для решения проблем, возникающих в повседневной жизни. Ценность математики заключается еще и в том, что она содержит укрупненные единицы информации, которые развивают человека разумного в еще более разумного – в индивидуально мыслящую личность с индивидуальными особенностями поведения [1].
Реализация математической подготовки студентов технического вуза предусматривает построение процесса обучения с учетом требований нормативных документов, потребностей профессиональной деятельности будущих инженеров. Федеральные государственные образовательные стандарты высшего образования по направлению подготовки 21.03.01 «Нефтегазовое дело», утвержденные приказом Министерства образования и науки от 12 марта 2015 года, поддерживают компетентностный подход в обучении студентов и ориентированы на формирование умений и опыта применения полученных математических знаний в будущей профессиональной деятельности.
Э.Ф. Зеер компетентностный подход определяет как приоритетную ориентацию на такие цели-векторы образования, как: обучаемость, самоопределение, самоактуализацию, социализацию и развитие индивидуальности студента [5]. Сегодня противоречие между необходимостью передачи информации каждому субъекту в соответствии с его учебно-познавательными возможностями и отсутствием условий для такой передачи при фронтальном обучении может быть устранено путем проектирования индивидуальной траектории обучения каждого отдельно взятого студента [9]. Практика преподавания математики показывает, что студент может продвигаться по собственной траектории образования, если ему будут предоставлены следующие возможности:
ставить собственные цели в изучении конкретной темы;
выбирать оптимальные формы и темпы обучения;
учиться в соответствии с его индивидуальными особенностями;
осмысливать полученные результаты образования;
оценивать и корректировать свою деятельность [там же].
При этом структура и содержательные основы дисциплины должны быть сохранены, обеспечено достижение студентом нормативного образовательного уровня. В филиале Уфимского государственного нефтяного технического университета в г. Октябрьском с целью формирования математических компетенций студентов преподаватели активно используют в своей деятельности различные педагогические технологии: технологию развития критического мышления, case-study, интерактивные лекции, включение студентов в проектную деятельность [3, 9, 10]. В настоящее время усилия преподавателей математики направлены на создание сборника прикладных задач по нефтегазовому делу на междисциплинарной основе. В этот сборник предполагается включить теоремы, выводы интересных формул, которые были получены в ходе совместной работы студентов и преподавателей, а также результаты проектной деятельности студентов [3, 7]. В данной статье авторы предлагают один из таких творческих подходов к усвоению теоретического материала дисциплин «Математика» и «Механика сплошных сред». Предлагаемый ниже материал может быть использован также при подготовке студентов к научно-практической конференции.
Обычно векторный потенциал 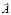 соленоидального вектора
соленоидального вектора 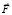 определяют по формуле
определяют по формуле
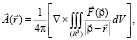 (1)
(1)
в которой интегрирование ведётся по всем точкам трёхмерного пространства [4]. Однако существует другой способ определения декартовых координат вектора 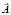 с помощью одномерных интегралов от декартовых координат вектора
с помощью одномерных интегралов от декартовых координат вектора 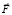 .
.
Рассмотрим вектор 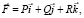 дивергенция которого равна нулю,
дивергенция которого равна нулю, 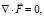 т.е.
т.е.
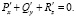 (2)
(2)
Допустим, что требуется найти вектор 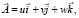 удовлетворяющий условию
удовлетворяющий условию
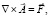 (3)
(3)
или, в декартовых координатах,
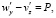 (4)
(4)
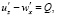 (5)
(5)
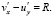 (6)
(6)
Для упрощения решения последней системы уравнений положим, что w = 0 Из (4) и (5) получим
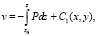 (7)
(7)
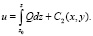 (8)
(8)
Подстановка значений (7), (8) в (6) даёт:
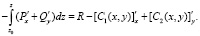
С помощью (2) это равенство приводится к
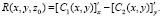 (9)
(9)
Пусть С2 (х, у) = 0, тогда равенство (8) примет вид
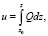
а из (9) получим:
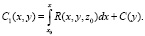
Положим C(y) = 0. Выражение (7) запишется так:
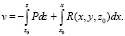
В итоге
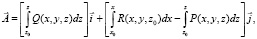 (10)
(10)
где x0, z0 – произвольные константы.
При выводе формулы (10) мы полагали, что С2 (х, у) = 0, C(y) = 0. Однако мы могли бы взять С2 (х, у) = C(x) и отказаться от условия C(y) = 0. В этом случае будем иметь:
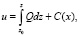
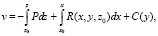
и 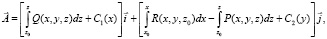
где С1(х), С2(y) – произвольные функции. Возможны и другие варианты выбора функции С2 (х, у). Таким же путём можно получить формулы:
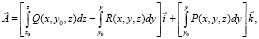 (11)
(11)
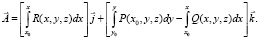 (12)
(12)
Как видим, для определения векторного потенциала достаточно найти одномерные интегралы от координат соленоидального вектора 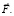
Отметим, что векторный потенциал, вычисляемый по формулам (10)–(12), не всегда является соленоидальным, тогда как формула (3) пригодна для нахождения лишь соленоидальных векторов. Рассмотрим два примера использования полученных результатов.
Пример 1. Найти векторный потенциал вектора 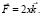
Решение: равенство 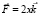 означает, что P = Q = 0, R = 2x. Ради простоты положим x0 = y0 = z0 = 0. По формуле (11) получим вектор
означает, что P = Q = 0, R = 2x. Ради простоты положим x0 = y0 = z0 = 0. По формуле (11) получим вектор 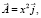 а формула (12) даст другой векторный потенциал
а формула (12) даст другой векторный потенциал 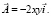 Нетрудно убедиться, что ротор обоих векторов одинаков:
Нетрудно убедиться, что ротор обоих векторов одинаков: 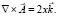 Попытка рассчитать векторный потенциал по формуле (1) приводит к расходящемуся интегралу
Попытка рассчитать векторный потенциал по формуле (1) приводит к расходящемуся интегралу
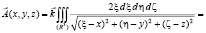
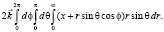
Заметим, что для соленоидального вектора справедлива формула Стокса
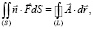 (13)
(13)
где векторный потенциал 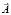 подчиняется условию (2).
подчиняется условию (2).
В учебной литературе формулу Стокса [6] применяют, как правило, для вычисления циркуляции вектора 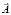 путём вычисления левой части формулы (13). Однако ею практически не пользуются при вычислении потока вектора
путём вычисления левой части формулы (13). Однако ею практически не пользуются при вычислении потока вектора 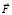 с помощью вычисления правой части формулы (13). Иначе говоря, в формуле (13) вычисление левого интеграла не сводят к вычислению правого. Формулы (10)–(12) позволяют решать и такие задачи. Поскольку соотношение (13) инвариантно, то неоднозначность задания вектора
с помощью вычисления правой части формулы (13). Иначе говоря, в формуле (13) вычисление левого интеграла не сводят к вычислению правого. Формулы (10)–(12) позволяют решать и такие задачи. Поскольку соотношение (13) инвариантно, то неоднозначность задания вектора 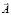 не сказывается на величине его циркуляции.
не сказывается на величине его циркуляции.
Пример 2. Вычислить поток вектора 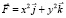 сквозь круг (S):x2 + y2 ≤ 1, z = 0.
сквозь круг (S):x2 + y2 ≤ 1, z = 0.
Решение. Учитывая, что нормальный к (S) вектор 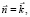 имеем:
имеем: 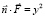 , и мы сразу получаем:
, и мы сразу получаем:
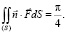
Найдём этот же поток с помощью циркуляции по правой части формулы (13). Вектор 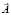 определим по формуле (10), в которой положим x0 = z0 = 0. Равенство
определим по формуле (10), в которой положим x0 = z0 = 0. Равенство 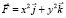 означает, что P = 0, Q = x2, R = y2, поэтому по формуле (10) получим
означает, что P = 0, Q = x2, R = y2, поэтому по формуле (10) получим 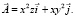 Тогда
Тогда 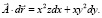 Так как круг (S) ограничен окружностью
Так как круг (S) ограничен окружностью 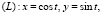
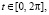 лежащей на плоскости z = 0, то
лежащей на плоскости z = 0, то
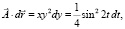
отсюда
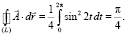
Результативность обучения в техническом вузе повысится, если у студентов последовательно развивать умение приводить оценочные показатели различных характеристик к компактному и обозримому виду статистических величин, грамотно интерпретировать их. Для этого они должны обладать логико-математической компетентностью, сформированность которой и позволяет системно видеть педагогический процесс, успешнее анализировать педагогические ситуации, находить закономерности рассматриваемых явлений, выделять цель и главные задачи, делать адекватные выводы [1]. Математика – вершина натурфилософии – абстрактное обобщенное описание явлений объективной действительности, поэтому она не придаток, язык или средство, а именно источник всех других знаний [13].



