Использование смешанных материалов значительно возросло за последнее время. Основное преимущество заключается в том, что их теплотехнические свойства отвечают насущным потребностям, и специалистов это особенно интересует. Легко поддающиеся изменению тепловые свойства смешанных материалов в такой же степени могут быть важными для их использования при изоляции трубопроводов. Разница коэффициентов теплопроводности в различных направлениях может привести к тепловому напряжению, поэтому авторы уделяли особое внимание тепловому режиму при теплоизоляции цилиндра, изготовленного с ортотроповым слоем.
Из анализа нормативных расчетных и фактических потерь теплоты трубопроводами выявлены значительные расхождения [4, 5]. В связи с этим и на основании проведенных исследований авторами была опубликована серия работ по температурным режимам в изоляции трубопроводов различных назначений и разных типов прокладок [1, 2, 3, 7].
В современных проектах используют несколько слоев из различных комбинированных материалов. Каждый из этих слоев рассчитан так, чтобы выдержать структурные, тепловые и химические нагрузки, которым может подвергаться конечный продукт. Существует необходимость изучать многослойный ортотропный цилиндр, включая теплопередачу внутренних слоев и всего цилиндра. С такими вопросами сталкиваются при конструировании цистерн для хранения химических веществ, прокладке нефте- и газопроводов. Использование наложения и распада системы Фурье позволило в исследовании применить комплексные графики распределения температуры. Для постановки задачи были приняты основные положения из теории теплообмена [6].
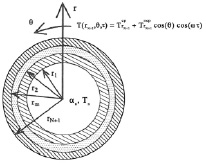
Рис. 1. Схема цилиндра
Материалы и методы исследования
На рис. 1 показана схема цилиндра и основных пограничных с ним состояний. Двухмерное нестационарное уравнение теплопроводности для энного ортотропного слоя следующее (1). Ортотропия – неодинаковость физических свойств среды по двум (трем) взаимно перпендикулярным направлениям внутри этой среды и является частным случаем анизотропии.
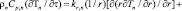
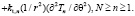 (1)
(1)
Теплопередача обусловливается частными дифференциальными уравнениями в зависимости от количества слоев (N). Требуемые пограничные условия следующие:
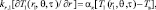 (2)
(2)
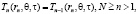 (3)
(3)
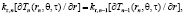
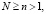 (4)
(4)
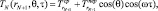 (5)
(5)
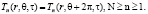 (6)
(6)
где ρn – плотность материала цилиндра; Cp,n – теплоемкость материала; T – температура; τ – время; k – коэффициент теплопроводности; r – радиус; θ – угол; N – количество слоев; N + 1 – внешний радиус цилиндра; n – номер слоя; r – радиальное направление; t – тангенциальное направление; Tв – температура, при которой происходит конвекция во внутреннем радиусе цилиндра; r1 – внутренний радиус цилиндра; ω – частота изменяющейся температуры; 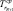 – средняя температура на внешнем радиусе цилиндра;
– средняя температура на внешнем радиусе цилиндра; 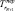 – величина изменяющейся температуры на внешнем радиусе цилиндра; αK – коэффициент конвекции.
– величина изменяющейся температуры на внешнем радиусе цилиндра; αK – коэффициент конвекции.
Для достижения постоянной циклической теплопроводности не требуется никакого начального условия. 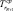 и Tв были взяты равными нулю, чтобы упростить решение, но это упрощение влияет на потерю всеобщего характера такого решения для циклических компонентов. Влияние
и Tв были взяты равными нулю, чтобы упростить решение, но это упрощение влияет на потерю всеобщего характера такого решения для циклических компонентов. Влияние 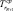 и Tв на общее распределение температуры заключается в использовании наложения. Авторы определяли следующие безразмерные группы:
и Tв на общее распределение температуры заключается в использовании наложения. Авторы определяли следующие безразмерные группы:
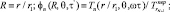

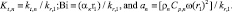
Используя эти группы, уравнения (1)–(5) переписываем следующим образом:
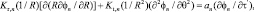 (7)
(7)
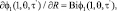 (8)
(8)
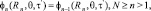 (9)
(9)
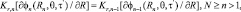 (10)
(10)
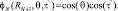 (11)
(11)
Решение к 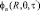 может быть найдено путем определения вспомогательной задачи
может быть найдено путем определения вспомогательной задачи 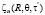 . Объединяя
. Объединяя 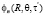 с
с 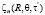 получаем:
получаем:
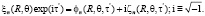 (12)
(12)
где R – безразмерный радиус; K – безразмерный коэффициент теплопроводности; Bi – число Био; ? – безразмерная температура; αn – безразмерная частота; ζn – добавочная безразмерная температура; 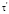 – безразмерное время.
– безразмерное время.
Применив пограничные условия и осуществив определенные математические вычисления, получаем решение для энного слоя:
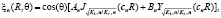 (13)
(13)
где 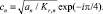 Температура и радиальная теплопроводность в энном слое, соответственно:
Температура и радиальная теплопроводность в энном слое, соответственно:
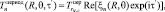 (14)
(14)
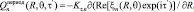 (15)
(15)
где 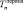 ,
, 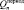 – температура и радиальная теплопроводность в энном слое; A – комплексная постоянная; B – комплексная постоянная; J – комплексная функция Бесселя первого рода; exp – показатель к основанию e; Re – действительная часть комплексной величины между скобками; ξn – пространственная часть комплекса безразмерной температуры.
– температура и радиальная теплопроводность в энном слое; A – комплексная постоянная; B – комплексная постоянная; J – комплексная функция Бесселя первого рода; exp – показатель к основанию e; Re – действительная часть комплексной величины между скобками; ξn – пространственная часть комплекса безразмерной температуры.
Результаты исследования и их обсуждение
Циклическая радиальная теплопроводность в цилиндре, состоящем из N слоев, зависит от 4N параметров. Сочетание важных параметров быстро возрастает с ростом количества слоев. Как простой пример приведен двухслойный цилиндр. Двухслойный цилиндр может состоять из слоя, который несет структурную нагрузку, и изоляционного слоя. Такой подход помогает достичь структурной целостности первого слоя при наличии внешних тепловых нагрузок.
Величины во внутреннем слое n = 1 были установлены на a1 = 3,0, R2 = 1,5 и Kt,1 = 2,0, Kr,1 = 1,0 по определению. Переменные величины параметров во внешнем слое представлены в виде коэффициентов относительно величин во внутреннем слое. Четыре новых параметра определены как следующие: коэффициент плотности x ≡ (R3 – R2)/(R2 – R1), радиальный коэффициент проводимости 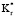 = Kr,2/Kr,1, тангенциальный коэффициент проводимости
= Kr,2/Kr,1, тангенциальный коэффициент проводимости 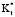 = Kt,2/Kt,1 и коэффициент частоты a* = a2/a1. Индекс коэффициента используется для определения порядка, в котором расположены слои. Если внешний слой сделан из изоляционного материала, то
= Kt,2/Kt,1 и коэффициент частоты a* = a2/a1. Индекс коэффициента используется для определения порядка, в котором расположены слои. Если внешний слой сделан из изоляционного материала, то 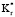 < 1,0 и наоборот. Подобные аргументы применены к
< 1,0 и наоборот. Подобные аргументы применены к 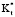 , a*.
, a*.
Результаты зависят от величин радиальной теплопроводности во внутреннем (Qm,1) и поверхностном (Qm,2) радиусах. Qm,2 важна при рассмотрении изменения свойств для внутреннего слоя, когда теплота достигает его через внешний слой. Несколько значений х было использовано. Значения х показаны на рис. 2. Следующие относительные величины были использованы (кроме изучаемого параметра): 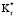 = 2,0;
= 2,0; 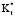 = 2,0; a* = 2,0 и Bi = 0,7.
= 2,0; a* = 2,0 и Bi = 0,7.
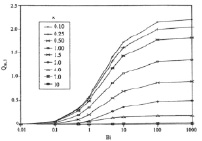
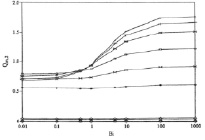
Рис. 2. Влияние Bi на Qm,1 и Qm,2
Рис. 2 показывает изменение в Qm,1 и Qm,2 с Bi. Большое значение Bi указывает на то, что внутренний слой имеет низкий kr и/или высокий αK. Более высокий Bi влияет на более низкое радиальное теплопроводное сопротивление во внутреннем слое. Общее радиальное теплопроводное сопротивление является суммой сопротивлений обоих слоев. Т.к. 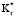 – величина постоянная, сопротивление внешнего слоя увеличивается с х. При низкой х радиальное сопротивление соответствует главным образом внутреннему слою. Таким образом, величины Qm,1 и Qm,2 значительно изменяются с Bi при низкой х. Для х > 2,0 сопротивление внешнего слоя преобладает, и влияние Bi на радиальную теплопроводность уменьшается. Для х > 4,0 Bi не оказывает значительного влияния на Qm,1 и Qm,2.
– величина постоянная, сопротивление внешнего слоя увеличивается с х. При низкой х радиальное сопротивление соответствует главным образом внутреннему слою. Таким образом, величины Qm,1 и Qm,2 значительно изменяются с Bi при низкой х. Для х > 2,0 сопротивление внешнего слоя преобладает, и влияние Bi на радиальную теплопроводность уменьшается. Для х > 4,0 Bi не оказывает значительного влияния на Qm,1 и Qm,2.
Рис. 3 показывает влияние a* на Qm,1 и Qm,2. Для x < 1,0 изменение в Qmi и Qm,2 с a* различные. При низкой х теплота, проходящая через внешний слой, слегка возрастает с a*, в то время как оно остается относительно постоянным или падает во внутреннем слое. Такой результат подтверждает изоляционное влияние внутреннего слоя с определенными 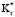 и
и 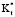 . Когда х > 1,0 как Qm,1, так и Qm,2 уменьшаются с a*. Скорость уменьшения Qm,1 с a* больше, чем у Qm,2, что подтверждает изоляционные свойства внутреннего слоя для данных относительных значений.
. Когда х > 1,0 как Qm,1, так и Qm,2 уменьшаются с a*. Скорость уменьшения Qm,1 с a* больше, чем у Qm,2, что подтверждает изоляционные свойства внутреннего слоя для данных относительных значений.
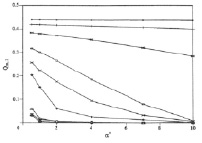
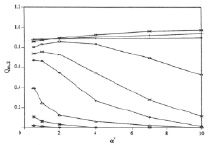
Рис. 3. Влияние a* на Qm,1 и Qm,2. Примечание: пометки сверху * – параметр относительно его величины во внутреннем слое
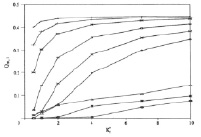
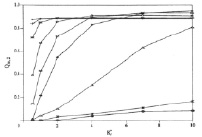
Рис. 4. Влияние K*r на Qm,1 и Qm,2
Рис. 4 показывает влияние 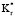 на Qm,1, и Qm,2. Если
на Qm,1, и Qm,2. Если 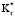 < 1,0, это означает, что внешний слой обеспечивает теплоизоляцию, в то время как, если
< 1,0, это означает, что внешний слой обеспечивает теплоизоляцию, в то время как, если 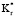 > 1,0, то внутренний слой является изолятором. Радиальное сопротивление теплопроводности в слое прямо пропорционально х и обратно пропорционально
> 1,0, то внутренний слой является изолятором. Радиальное сопротивление теплопроводности в слое прямо пропорционально х и обратно пропорционально 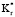 , т.к. величины во внутреннем слое постоянны, радиальное сопротивление теплопроводности внутреннего слоя остается постоянным при различных
, т.к. величины во внутреннем слое постоянны, радиальное сопротивление теплопроводности внутреннего слоя остается постоянным при различных 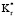 . Общее сопротивление цилиндра изменяется с изменением сопротивления внешнего слоя. Низкий
. Общее сопротивление цилиндра изменяется с изменением сопротивления внешнего слоя. Низкий 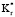 означает, что внешний слой является изолятором. Низкий
означает, что внешний слой является изолятором. Низкий 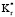 с относительно плотным внешним слоем (например, х > 0,5) приводит к значительным увеличениям in Qm,1 и Qm,2. Если снижение значений радиальной теплопроводности увеличивается, то плотность внешнего слоя также увеличивается. При высоком
с относительно плотным внешним слоем (например, х > 0,5) приводит к значительным увеличениям in Qm,1 и Qm,2. Если снижение значений радиальной теплопроводности увеличивается, то плотность внешнего слоя также увеличивается. При высоком 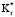 вклад внешнего слоя в общее радиальное теплосопротивление значителен только тогда, когда он сопровождается высотой х. Таким образом, значения Qm,1 и Qm,2 не зависят от изменения
вклад внешнего слоя в общее радиальное теплосопротивление значителен только тогда, когда он сопровождается высотой х. Таким образом, значения Qm,1 и Qm,2 не зависят от изменения 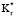 > 4 и х < 0,5.
> 4 и х < 0,5.
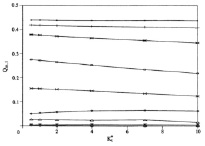
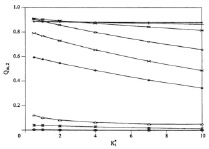
Рис. 5. Влияние K*t на Qm,1 и Qm,2
Рис. 5 показывает влияние 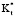 на Qm,1 и Qm,2. Переменный
на Qm,1 и Qm,2. Переменный 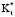 не имеет значительного влияния на Qm,1. Главной причиной изменений в Qm,1 является х. Влияние
не имеет значительного влияния на Qm,1. Главной причиной изменений в Qm,1 является х. Влияние 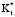 на Qm,2 ограничивается 0,5 < х < 2,0. В этой цепочке увеличение
на Qm,2 ограничивается 0,5 < х < 2,0. В этой цепочке увеличение 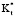 отражается в снижении в Qm,2. Более высокое значение
отражается в снижении в Qm,2. Более высокое значение 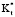 означает более низкое тангенциальное сопротивление теплопроводности, и большее количество теплоты, проходящего через внешнюю стенку цилиндра, будет проведено в тангенциальном, а не в радиальном направлении. Низкая х вызывает низкое тангенциальное сопротивление независимо от
означает более низкое тангенциальное сопротивление теплопроводности, и большее количество теплоты, проходящего через внешнюю стенку цилиндра, будет проведено в тангенциальном, а не в радиальном направлении. Низкая х вызывает низкое тангенциальное сопротивление независимо от 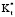 . Аналогично, высокое значение x вызывает высокое тангенциальное сопротивление независимо от
. Аналогично, высокое значение x вызывает высокое тангенциальное сопротивление независимо от 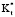 .
.
Выводы
При анализе нормативных, расчетных и фактических потерь теплоты трубопроводами выявлены значительные расхождения. В связи с этим и на основании проведенных исследований авторами была опубликована серия работ по температурным режимам в изоляции трубопроводов различных назначений и разных типов прокладок [1–4].
1. В результате аналитического вычисления получены зависимости (14) и (15), позволяющие определить температуру и радиальную теплопроводность в энном слое (n).
2. Аналитически решены вопросы теплопроводности в многослойном двухмерном ортотроповом цилиндре, взаимосвязанные с ассиметричным и циклическим распределением температуры во внешней стенке.
3. Из теории теплообмена авторы показали, что теплопроводность через цилиндр является функцией числа Био и следующих четырех безразмерных параметров в каждом слое: коэффициента частоты (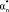 ), коэффициента плотности (
), коэффициента плотности (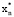 ), а также радиального (
), а также радиального (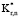 ) и тангенциального (
) и тангенциального (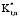 ) коэффициентов проводимости. Были построены графики зависимости.
) коэффициентов проводимости. Были построены графики зависимости.
Исследования выполнялись на основании целевой и комплексной программы «Нефть и газ Западной Сибири».



