При разработке цифровых систем автоматического регулирования (рис. 1) модели, методы и алгоритмы формирования управляющих воздействий подбираются таким образом, чтобы обеспечить требуемую динамику процесса регулирования [2, 4–6].

Различные алгоритмы цифрового регулирования могут формировать разные управляющие воздействия, что приводит к необходимости проведения в такте управления превентивных оценок реакции объекта управления. Это легло в основу построения метода смешанного цифрового регулирования [3], воплощенного в программе реализации унифицированных алгоритмов наилучшего цифрового регулирования (рис. 2) [1].

В методе смешанного цифрового регулирования [3] для формирования управляющего воздействия в текущий момент времени Uсм(nT) вычисляются управляющие воздействия по различным алгоритмам цифрового регулирования:

U1(nT, Uсм((n – 1)T),

xсм(nT), xсм((n – 1)T),…),

…,

UN(nT, Uсм((n – 1)T),

xсм(nT), xсм((n – 1)T),…),

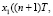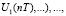
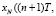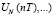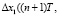
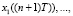
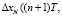
моделируется реакция объекта управления на каждое сформирование управляющего воздействия ( xсм(nT), xсм(nT) ), рассчитывается невязка ( 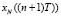) и выбирается алгоритм формирования управляющего воздействия, который привел к минимальному значению рассогласования:

… … …

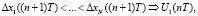
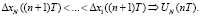
Рис. 1. Пример схемы замкнутой системы автоматического регулирования (САР), где: t – время ( для цифровой САР t = nT, n = 0, 1, 2,…, T – время реакции объекта управления); x0 – задающее воздействие, ?x(t) – рассогласование (отклонение, ошибка) в текущий момент (?x(t) пропорционален x0 – x(t)), U(t) – управляющее воздействие, x(t) – регулируемая величина, ЭС – элемент сравнения

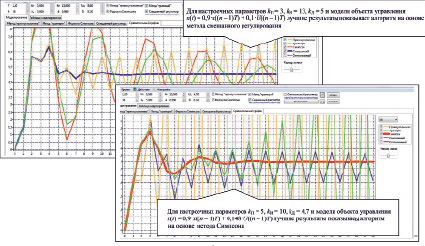
Рис. 2. Скриншоты программы реализации унифицированных алгоритмов наилучшего цифрового регулирования [1]

Экспериментирование с программным инструментарием [1] показало, что метод смешанного цифрового пропорционально-интегрально-дифференциального (ПИД) регулирования, показывая в основном существенно лучшие результаты, в отдельных обстоятельствах приводит к неудачной динамике (рис. 2). Чтобы избежать таких ситуаций, можно попробовать дополнительно отслеживать динамику каждого алгоритма цифрового регулирования, вошедшего в основу построения алгоритма смешанного управления, что делает актуальным вопросы построения метода, основанного на выборе алгоритма на каждом шаге регулирования и приводит фактически к построению оптимального метода цифрового регулирования.

Для улучшения качества цифрового регулирования в работе предложен метод оптимального регулирования и показано его удачное применение.

Метод цифрового оптимального регулирования:

I. Выбрать математические модели цифрового регулирования:

,

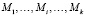где k – количество математических моделей цифрового регулирования.

II. Задать настроечные параметры и уставку.

III. В текущий момент времени t = nT по выбранным математическим моделям 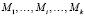рассчитать управляющие воздействия, каждое из которых зависит только от параметров своего процесса:

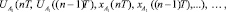
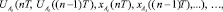
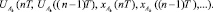
IV. Смоделировать в следующий момент времени 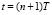реакции объекта управления на соответствующие управляющие воздействия:

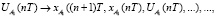
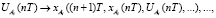
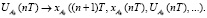
V. Рассчитать рассогласования:

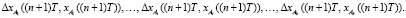
VI. Выбрать минимальное абсолютное значение ошибки:

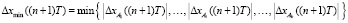
и соответствующую математическую модель формирования управляющего воздействия:

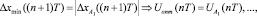
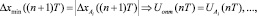
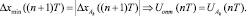
Алгоритм цифрового оптимального ПИД регулирования с параллельными вычислениями:

I. Базовые алгоритмы цифрового ПИД регулирования: 1) на основе математической модели ПИД регулирования с раскрытием интеграла по формуле «прямоугольников» (Aпр) [2, 3]; 2) на основе метода цифрового ПИД регулирования с представлением интеграла по формуле «трапеций» (Aтр) [2, 3]; с) на базе метода ПИД регулирования с раскрытием интеграла по формуле Симпсона (AС) [3].

II. Задание настроечных параметров (kП, kИ, kД) и уставки х0.

III. Формирование управляющих воздействий по выбранным алгоритмам цифрового ПИД регулирования:

III. 1. Если n = 0 (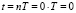), то:

III. 1.1. Невязка ().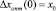

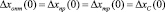III. 1.2. Вычисление управляющего воздействия:

().

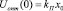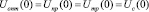III. 2. Если n = 1 (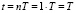), то:

III. 2.1. Формирование невязки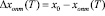

();

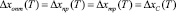III. 2.2. Параллельное вычисление управляющих воздействий:

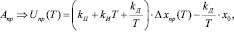
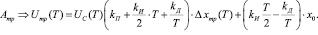
III. 3. Если n = 2 (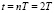), то:

III. 3.1. Параллельное формирование значений рассогласований: , .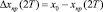

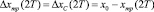III. 3.2. Параллельное вычисление управляющих воздействий:

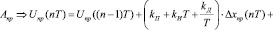
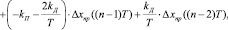(1)

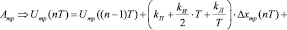
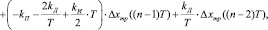(2)

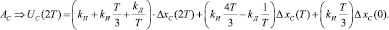
III. 4. Если n > 2 (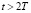), то:

III. 4.1. Параллельное формирование значений рассогласований: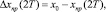

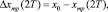
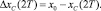
III. 4.2. Параллельное вычисление управляющих воздействий:

III. 4.2.1. Для , :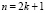

.

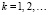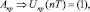
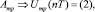
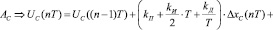
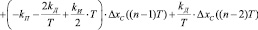III. 4.2.2. Для n = 2k, :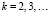

.

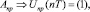
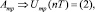
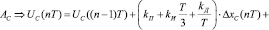
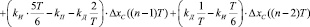IV. Параллельное моделирование реакций объекта управления в момент времени 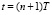на соответствующие управляющие воздействия:

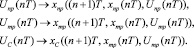
V. Параллельное моделирование рассогласований:

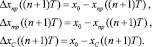
VI. Выбор алгоритма расчета управляющего воздействия для t = nT, соответствующего минимальному смоделированному абсолютному значению невязки для :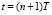

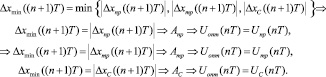
Моделирование оптимального цифрового ПИД регулирования

Метод оптимального цифрового регулирования поддерживается программой реализации унифицированных алгоритмов наилучшего цифрового регулирования (рис. 3) [1].

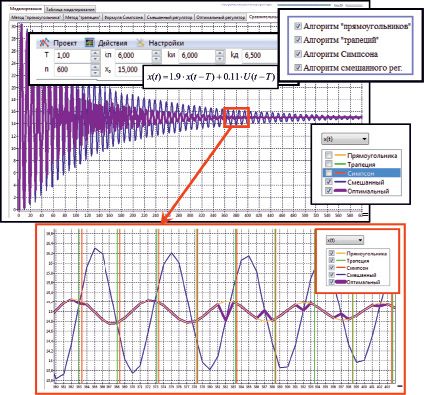
Рис. 3. Программный инструментарий оптимального ПИД регулирования [1]

Основные результаты:

1) предложен метод оптимального цифрового регулирования на основе моделей ПИД регулятора, отличающийся формированием наилучшего управляющего воздействия в такте превентивной оценки реакции объекта управления;

2) предложен алгоритм регулирования на базе построения параллельных вычислений управляющих воздействий и оценки динамики изменения регулируемого параметра по каждому процессу, отличающийся совместным использованием традиционных алгоритмов регулирования с учётом возможности применения алгоритмов смешанного регулирования на каждом шаге обработки регулируемого параметра.

Исследование выполнено при поддержке ФГБОУ ВО «ПГУ» по теме «Разработка программной системы поддержки процесса управления в предаварийных состояниях для восстановления нормальной работы», приказ №7-н/26 от 23.10.2013 г.