Scientific journal
Modern high technologies
ISSN 1812-7320
"Перечень" ВАК
ИФ РИНЦ = 0,940

Personal portfolio

THE JUSTIFICATION POSSIBILITY OF THE PIPELINE UNDERGROUND LAYING IN PERMAFROST AREAS

Tarasenko A.A. 1 Redutinskiy M.N. 2 Chepur P.V. 1
1 Tyumen State Oil and Gas University
2 Giprong-Ecom, Tyumen
Article in PDF
2592 KB
In the issue changes depending on the stress-strain state of pipelines and settlement on the size of the zone of subsidence for pipe sizes, is most prevalent in the construction of main oil pipelines (530х10, 820х12, 1020х12, 1020х14, 1020х16, 1220х14, 1220х16, 1220х18 mm). To determine the true value of the stress in the pipe wall, as well as the exact location of maximum stress for a range of zones of subsidence from 5 to 60 meters. To do this, the authors developed a finite element model of the pipeline that takes into account real interaction with a soil pipe base and allows to calculate the stress-strain state structure in the variable area of subsidence. On the basis of these relationships for the underground laying of pipelines in areas where permafrost offered to artificially limit the zone of possible subsidence by dividing device supports from the ground with higher construction properties and physical and mechanical properties. This solution would significantly reduce costs in the construction of new pipelines in the areas with permafrost.
pipelines
oil pipeline
settlement
permafrost
frost
fem
ansys
stress-strain state
strength
stress
ground
base

Постепенное снижение дебета месторождений углеводородов, введенных в эксплуатацию в середине прошлого века в Тюменской области, дало толчок к освоению ресурсов арктического региона и Восточной Сибири. Строительство объектов инфраструктуры магистрального транспорта нефти в данных районах осложняется повсеместным распространением многолетнемерзлых грунтов (ММГ), а также грунтов с низкими строительными свойствами и физико-механическими показателями [4, 5], обусловленными их переувлажнением. Согласно регламентирующим документам [6] ММГ в качестве основания под инженерно-технические сооружения могут быть использованы по двум принципам: I – ММГ используются в мерзлом состоянии, сохраняемом в процессе строительства и в течение всего периода эксплуатации сооружения; II – ММГ используются в оттаянном или оттаивающем состоянии.

В статье [2] указывается на существующие противоречия в регламентирующих документах [6] и [7], являющихся основными при проектировании объектов трубопроводного транспорта в районах распространения ММГ. В [6] отмечено, что сохранение грунта под сооружением в мерзлом состоянии целесообразно при экономически обоснованных затратах. В противном случае рекомендовано использование ММГ по II принципу. Согласно [7] основным принципом использования ММГ в качестве основания под трубопроводом является принцип их сохранения в мерзлом состоянии. Магистральные нефтепроводы согласно [6] относятся к горячим трубопроводам, т.к. транспортируют нефть только при положительной температуре. Таким образом, при сооружении магистральных нефтепроводов выполнение требований [7] возможно только при надземном способе прокладки. Данное техническое решение приводит к увеличению затрат на строительство в 2,5–4 раза [2], что при сооружении протяженных объектов значительно снижает общую рентабельность проекта. В нормативном документе [7] не приводится обоснование необходимости сохранения грунтов под нефтепроводом в мерзлом состоянии [2].

В действующих нормативных документах [6–7] не дается четких и обоснованных рекомендаций по выбору способа прокладки трубопроводов и принципу использования ММГ в качестве их основания. В [2] на основе анализа регламентирующих документов сделан вывод, что при подземной прокладке на ММГ опасаются значительных осадок трубы при оттаивании грунтов. В [7] величина осадок трубопроводов не ограничивается, а регламентируются только напряжения, возникающие в трубопроводе. Проведенные натурные исследования на трассах нефтепроводов, проложенных в болотистой местности [2], показали, что осадка при длительной эксплуатации может достигать 0,5 м без существенного изменения напряженно-деформированного состояния (НДС) трубопровода.

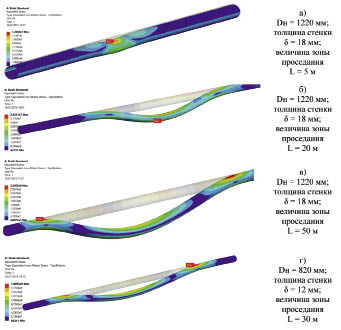
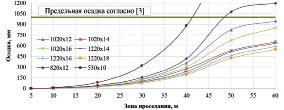
Наиболее опасными при подземной прокладке трубопроводов на ММГ являются участки перехода основания от грунтов с высокой несущей способностью к оттаивающим грунтам с низкими физико-механическими характеристиками. С научной и практической точки зрения, анализ изменения НДС трубопровода в этих зонах, а также определение предельных величин осадки в зависимости от длины зоны проседания представляет несомненный интерес. Исходя из этого, авторами были поставлены задачи: по результатам численного моделирования получить зависимости действующих эквивалентных напряжений в материале трубы от величины зоны проседания и определить значения максимально возможного провиса трубопровода при изменении зоны проседания. Для конечно-элементного анализа были выбраны трубы следующих диаметров, получившие наибольшее распространение при сооружении магистральных нефтепроводов: 530х10, 820х12, 1020х12, 1020х14, 1020х16, 1220х14, 1220х16, 1220х18 мм.

По расчетной классификации трубопровод представляет собой бесконечную трубчатую балку [2], имеющую зоны упругого защемления по краям. Авторами статьи предложена и реализована расчетная схема, учитывающая воздействие гидростатической нагрузки от транспортируемого продукта, а также равномерно распределенной нагрузки от веса обвалования на оболочечную конструкцию трубопровода при развитии его поперечных деформаций, обусловленных наличием зон проседания.

Расчетная схема участка трубопровода представлена на рис. 1. Вес обвалования на стенку трубопровода рассчитывается путем умножения площади криволинейного сечения S1 на длину трубы.

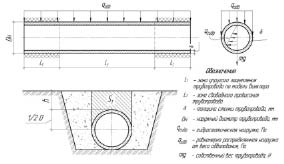
taras1.tif

Рис. 1. Расчетная схема участка трубопровода

С использованием программного комплекса ANSYS была создана конечно-элементная модель участка трубопровода согласно предложенной расчетной схеме. Трубопровод моделировался при помощи оболочечных конечных элементов SHELL181 и является телом вращения. Свойства стали заданы с учетом нелинейных свойств деформирования по реальной диаграмме «напряжения-деформации». Граничные условия определяются упруго-контактным взаимодействием концевых участков стенки трубопровода с грунтом. Свойства грунта задаются с помощью коэффициента постели по упрощенной модели – гипотезе Винклера. Установлено, что использование такой схемы приводит к удовлетворительной сходимости решения, что подтверждено тестовыми расчетами. Упругое контактное взаимодействие стенки и грунта моделируется с помощью конечного элемента COMBIN14. Гидростатическая нагрузка от перекачиваемого продукта, приложенная к внутренней поверхности трубопровода, и равномерно распределенная нагрузка от веса обвалования, приложенная к его наружной поверхности, моделируется с помощью элементов SURF154.

В предлагаемой модели осадка трубопровода рассчитывалась для наихудшего случая свободного провисания при изменяемой длине зоны грунта со слабыми физико-механическими характеристиками (L3 на рис. 1). Модель трубопровода разбита на гексагональную сетку с линейным размером ребра ? = 10 мм.

Всего было выполнено 96 расчетов, в которых варьировались следующие параметры:

– величина приращения зоны проседания принята равной 5 метрам: таким образом, был получен массив данных изменения НДС трубопровода в интервале значений зоны проседания от 5 до 60 метров;

– параметры НДС всего интервала значений осадки были получены для 8 типов труб с различными диаметрами и толщинами стенки.

Для проверки адекватности конечно-элементной модели был проведен тестовый расчет прогиба однопролетного бескомпенсаторного балочного перехода по упрощенной расчетной схеме и выполнено сравнение с известным аналитическим решением. Наиболее подходящей для верификации является расчетная модель однопролетного бескомпенсаторного балочного перехода, описанная А.Б. Айнбиндером и А.Г. Камерштейном [1]. Предложенная ими расчетная схема балочного перехода основана на трудах С.П. Тимошенко, а дополняет их тем, что помимо эксплуатационных нагрузок учитывает и упругое взаимодействие массива грунта с прилегающими подземными участками трубопровода (рис. 4).

taras2.tif

Рис. 2. Расчетная схема однопролетного бескомпенсаторного балочного перехода

Данная методика позволяет определить величину стрелки прогиба трубопровода в середине пролёта:

tar01.wmf (1)

где q – поперечная нагрузка; L – длина пролета; EI – изгибная жесткость трубопровода; f1 – безразмерный параметр, являющийся функцией величины ?, характеризующей относительное защемление концов трубопровода 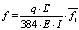[1].

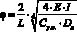tar02.wmf, (2)

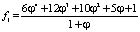tar03.wmf, (3)

где Dн – наружный диаметр трубопровода; Су.о. – обобщенный коэффициент нормального сопротивления грунта.

При верификации модели прикладывалась гидростатическая нагрузка от перекачиваемого продукта к внутренней поверхности трубопровода без учета веса обвалования. Расхождение аналитического решения и численного, методом конечных элементов, составило не более 3 %, что является хорошим результатом сходимости.

Авторами статьи была поставлена задача не только определить предельные величины прогибов трубопроводов различных типоразмеров в заданных интервалах зоны проседания, но и выявить точные места расположения зон повышенных напряжений. Актуальность такого подхода подтверждается тем, что в действующем нормативном документе [7] предельным параметром НДС трубы являются действующие напряжения, предельные величины перемещений не регламентированы. При несомненных достоинствах моделей С.П. Тимошенко и [1] и их практической ценности, данные аналитические решения не позволяют определять точные места концентрации напряжений и их значения в любой точке трубопровода – как в продольном, так и кольцевом направлениях. На рис. 3 приведены результаты расчета напряжений в нейтральном слое оболочки трубопровода длиной 140 м при различных задаваемых параметрах в соответствии с принятой расчетной схемой.

taras3.tif

Рис. 3. Распределение эквивалентных напряжений в нейтральном слое стенки трубопровода

Характер распределения напряжений в трубопроводе имеет различные черты для заданного интервала зон проседания и типоразмеров труб: при величинах зон проседания более 20 метров максимальные напряжения расположены на верхней образующей трубы, в случае, если величина зоны проседания менее 20 м, то максимальные напряжения концентрируются посередине нижней образующей трубопровода. Заметим, что при назначении граничных условий протяженности зоны проседания проводились оценочные расчеты, при которых определялся момент наступления предельного состояния, т.е. достижения значения предела текучести материала трубы. Современные нефтепроводы изготавливаются из труб класса прочности не ниже К56. Согласно [10] прочности К56 соответствуют стали, с пределом текучести не менее 410 МПа. Изгибная жёсткость трубопровода возрастает с увеличением наружного диаметра, поэтому предельные напряжения в теле трубы возникают при бо?льших значениях зоны проседания. Для трубопроводов диаметром 1020 мм это 47–50 метров в зависимости от толщины стенки, для 1220 мм – более 50 метров. У трубопровода диаметром 530 мм, за счет меньшей жесткости, предельное состояние возникнет существенно раньше. Так, на рис. 4 и 5 обобщены выполненные расчеты, на них представлены зависимости максимальных действующих напряжений в металле трубопроводов и их прогибы от величины зоны проседания.

В статье [3] указывается, что термопросадка трубопровода более 1,0 метра считается очень опасной и требует проведения противокарстовых мероприятий. В связи с этим, данное значение было принято в качестве предельного при определении значений провисов трубопровода, при том что в отечественной нормативной документации критерии предельных провисов магистральных трубопроводов не представлены.

Из графиков на рис. 4 и 5 видно, что при неравномерной осадке трубопровода предельные напряжения в стенке трубы на границе грунтов с разной несущей способностью наступят раньше, чем трубопровод достигнет предельного значения осадки. В связи с этим нецелесообразно принимать величину осадки, как критерий безопасной эксплуатации трубопровода.

taras5.tif

Рис. 5. Зависимости провиса трубопроводов от величины зоны проседания

Таким образом, проведенные расчеты, с учетом жесткости оболочечной конструкции трубопровода и свойств грунтового основания показали возможность подземной прокладки нефтепроводов в районах распространения ММГ.

Выводы

1. Авторами разработана конечно-элементная модель трубопровода, учитывающая реальное взаимодействие трубопровода с грунтовым основанием и позволяющая рассчитывать НДС конструкции при изменяемой зоне проседания. Свойства грунта задаются с помощью коэффициента постели по упрощенной модели – гипотезе Винклера. Проведенная верификация модели с известным аналитическим решением показала расхождение не более 3 %. Для реализации конечно-элементной модели использован программный пакет ANSYS.

2. В работе получены зависимости изменения напряженно-деформированного состояния и осадки трубопроводов от размеров зоны проседания для типоразмеров труб, получивших наибольшее распространение при сооружении магистральных нефтепроводов (530х10, 820х12, 1020х12, 1020х14, 1020х16, 1220х14, 1220х16, 1220х18 мм). Определены истинные значения напряжений в стенке трубопровода, а также точное месторасположение максимальных напряжений для интервала зон проседания от 5 до 60 метров.

3. Установлено, что при величинах зон проседания более 20 метров максимальные напряжения расположены на верхней образующей трубы, в случае, если величина зоны проседания менее 20 м, то максимальные напряжения концентрируются посередине нижней образующей трубопровода. Исследования показали, что нецелесообразно принимать величину осадки за критерий безопасной эксплуатации трубопровода, т.к. предельные напряжения наступают раньше, чем трубопровод достигнет предельного значения осадки.

4. На основе полученных зависимостей для подземной прокладки нефтепроводов в районах распространения ММГ предлагается искусственно ограничивать зону возможного проседания путем устройства разделительных опор из грунта с более высокими строительными свойствами и физико-механическими показателями. Данное техническое решение позволит существенно сократить затраты при сооружении новых нефтепроводов в районах ММГ.