Повышения эффективности эксплуатации конвейерного транспорта можно добиться, решая одновременно две задачи:
– разработка и внедрение автоматических систем управления скоростью движения конвейерной ленты в зависимости от параметров фактического грузопотока, поступающего на полотно конвейера;
– снижение износа движущегося полотна ленточного конвейера за счет поддержания оптимального соотношения между натяжениями в набегающей и сбегающей ветвях конвейерной ленты. При пуске и повышении скорости вращения приводных барабанов может возникать пробуксовка, которая увеличивает износ ленты и даже может привести к возгоранию при трении.
На кафедре «Автоматика и управление в технических системах» МГИ выполнены исследования по созданию такой системы управления скоростью движения ленты. Объектом управления в синтезируемой системе является электромеханическая система «управляемый электропривод – лента конвейера с грузом». В настоящее время рост грузопотоков и длин транспортирования обусловил широкое распространение высокопроизводительных конвейерных установок большой длины и мощности с двухдвигательным приводом. В данной статье рассматривается получение такой модели.
Общий принцип построения моделей движения ленты конвейера изложен в работах [5], [2], [3], [4]. Это принцип кусочно-линейной аппроксимации, который заключается в условном разбиении контура ленты на некоторое количество участков, в границах каждого из которых закон изменения скорости деформации по длине предполагается линейным. Расчетные схемы строятся с учетом некоторых допущений, изложенных в вышеперечисленных работах.
Расчетная схема конвейерной установки с двумя приводами и натяжным устройством в хвостовой части приведена на рис. 1. Система с распределенными параметрами аппроксимируется шестью сосредоточенными массами, три из которых (m1, m2, m3) расположены на грузовой ветви, две (m4, m5) – на порожней, а m6 представляет собой массу натяжного устройства. В качестве обобщенных переменных приняты координаты положения пяти масс (m1, m2, m3, m4, m5, m6), их скоростей (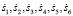 ), перемещения (
), перемещения (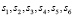 ), а также положение и скорость перемещения натяжного груза (
), а также положение и скорость перемещения натяжного груза (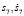 ). Конечномерная математическая модель движения конвейера с грузом описана четырнадцатью координатами состояния
). Конечномерная математическая модель движения конвейера с грузом описана четырнадцатью координатами состояния
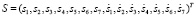 .
.
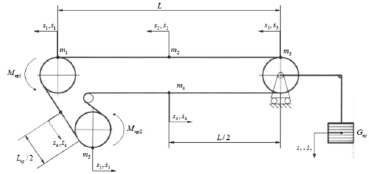
Рис. 1. Расчетная схема конвейера с двухдвигательным приводом
В основе построения математической модели положен метод Лагранжа второго рода:
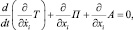 (1)
(1)
где Т – кинетическая энергия участка, П – потенциальная энергия участка, А – работа внешних сил на участке. В качестве обобщенных координат хi примем перемещения si и скорости перемещения 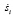 сосредоточенных масс mi, i = 1,2,…6.
сосредоточенных масс mi, i = 1,2,…6.
Кинетическая энергия ленты и груза, равномерно распределенного на соответствующем участке между точками i и j представлена выражением
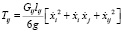 , (2)
, (2)
где Gij – вес ленты, роликоопор и груза на участке ij, lij – длина участка, g – ускорение свободного падения.
Потенциальная энергия ij участка длиной lij складывается из энергии упругих деформаций и потенциальной энергии замкнутого контура ленты с распределенной массой:
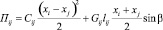 . (3)
. (3)
Здесь Cij – жесткость участка, b – угол наклона конвейера к горизонту.
Работа внешних сил на ij участке создается суммой сил сопротивления движению и движущей силы привода, которая определяется из выражений:
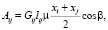
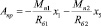 , (4)
, (4)
где μ – коэффициент сопротивления движению, Mn1 и Mn2 – движущие моменты приводов, приведенные к радиусу приводных барабанов, Rб2 и Rб1 – радиусы приводных барабанов.
Работа сил внутреннего трения на участке ij определяется в предположении, полагая, что силы внутреннего трения пропорциональны скоростям деформации:
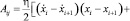
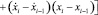 , (5)
, (5)
где η – коэффициент вязкости ленты.
Дальнейшая методика получения математической модели движения ленты конвейера подробно изложена в работах [1], [2], [3], [4], [5]. Систему дифференциальных уравнений, составляющих математическую модель, получим согласно выражению (1), выполнив необходимые подстановки и дифференциальные преобразования. Получим следующую запись системы дифференциальных уравнений, описывающих движение загруженной ленты:
1. 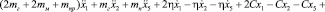
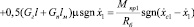
2. 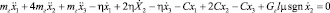 ;
;
3. 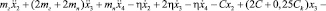
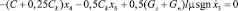 ; (6)
; (6)
4. 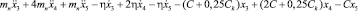
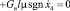 ;
;
5. 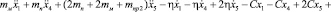
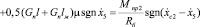 ;
;
6. 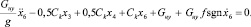
Последние преобразования позволят нам получить лаконичное матричное представление этой модели относительно вектора обобщенного перемещения 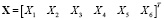 :
:
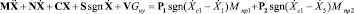 , (7)
, (7)
где
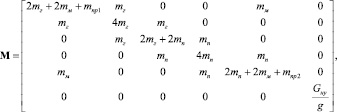

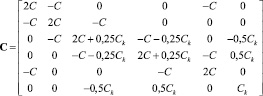 ,
,
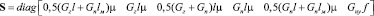 ,
,
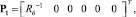
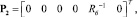
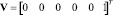 .
.
Далее умножим все члены выражения (6) на матрицу М–1 и введем в модель координаты состояния согласно каноническому правилу:
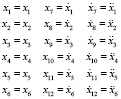
Модель движения конвейерной ленты в пространстве состояний представляется в виде системы нелинейных дифференциальных уравнений:
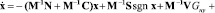
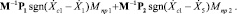 (8)
(8)
В данной системе внешними воздействиями являются движущие моменты, развиваемые приводами u1 = Mпр1 и 2 = Mпр2, силы сопротивления движению конвейерной ленты u3 = sgn x и вес натяжного устройства u4 = Gну. В этом случае матрица 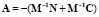 является матрицей состояния системы, а матрицы
является матрицей состояния системы, а матрицы 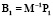 ,
, 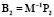 ,
, 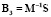 ,
, 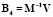 – матрицами управления. Система уравнений принимает вид:
– матрицами управления. Система уравнений принимает вид:
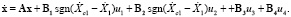 (9)
(9)
Матрицы состояния А и В и управления в модели являются блочными:
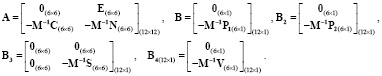
Составим матрицу управления 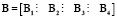 :
:
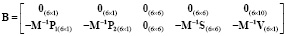 .
.
Моделирование движения ленты с грузом для двухприводного конвейера проводилось в Simulink. Были использованы блоки: State Space, позволяющий задать внутреннюю модель движения конвейерной ленты, Mux, объединяющий управляющие воздействия в вектор 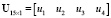 , для моделирования приводов используются готовые модели асинхронных короткозамкнутых приводов с частотно-векторным управлением, рассмотренные в работах [2], [3], [6]. Схема моделирования приведена на рис. 2. Моделирование проводилось для числовых значений:
, для моделирования приводов используются готовые модели асинхронных короткозамкнутых приводов с частотно-векторным управлением, рассмотренные в работах [2], [3], [6]. Схема моделирования приведена на рис. 2. Моделирование проводилось для числовых значений:
l = 1500 м, mг = 1518 кг, mn = 352 кг,
mпр1 = 3000 кг, mпр1 = 2000 кг, Mпр1 = 20900 Нм, Mпр2 = 20900 Нм, Rб = 0,5 м,
μ = 0,03, μ = 0,03, f = 0,3, C = 10000 H/м, Ск = 1010 H/м, Gну 52000 кг.
Результатами компьютерного моделирования явились переходные процессы по скоростям обобщенных координат ленты и натяжного устройства, представленные на рис. 3. Графики соответствуют режиму разгона и режиму работы конвейера с постоянной скоростью. Результаты моделирования позволяют определять скорости и натяжения в характерных точках ленточного конвейера, что даст возможность синтезировать систему управления скоростью движения конвейерной ленты при отсутствии пробуксовки на приводных барабанах и автоматически распределять нагрузку равномерно между приводами при любой скорости движения конвейера.
Рассмотрим теперь вопрос, связанный со стабилизацией величины тягового фактора. Повышение эффективности эксплуатации ленточного конвейера в большой степени связано со снижением износа движущегося полотна. При пуске и повышении скорости вращения приводных барабанов может возникать пробуксовка, которая увеличивает износ ленты и даже может привести к возгоранию при трении.
Известно, что эффект пробуксовки возникает, когда величина тягового фактора превышает значение, которое можно назвать критическим. Величина тягового фактора рассчитывается по формуле:
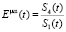 , (10)
, (10)
где S4 – натяжение в набегающей ветви, S1 – натяжение в сбегающей ветви.
Для однодвигательного ленточного конвейера с углом охвата лентой барабана α = π пробуксовка будет отсутствовать при условии Еμα ≤ 2,5. В случае с двухдвигательным приводом общий тяговый фактор будет равен произведению тяговых факторов на каждом из приводных барабанов, следовательно, должен быть Еμα ≤ 6,25. Добившись поддержания общего тягового фактора не выше данного уровня, мы сможем снизить вероятность возникновения пробуксовки на каждом отдельно взятом приводном барабане.
Используем для разработки системы стабилизации тягового фактора зависимости между его величиной и весом натяжного устройства конвейера. Согласно формуле (10) для получения тягового фактора необходимо знать натяжение в сбегающей ветви S1 и натяжение в набегающей ветви S4. При изменении скорости движения конвейера изменяются растяжения участков ленты Δ. Пусть Δ1 = s4 – s5 – это растяжение порожней ветви, и Δ4 = s1 – s2 – растяжение грузовой ветви. При изменении веса натяжного устройства изменяются деформации Δ1 и Δ4, а также значения натяжений S1 и S4, которые зависят от этих деформаций. С другой стороны, вычислить натяжения можно по формулам:
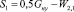 ,
,
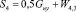 , (11)
, (11)
где W2,1 – сопротивление движению на порожней ветви, W4,3 – сопротивление движению на грузовой ветви.
Проведем тарирование конвейерной ленты, суть которого заключается в изменении веса натяжного устройства Gну и в одновременном расчете по формуле (11) натяжений, и снятии модельных данных о деформациях Δ. Вес натяжного устройства изменялся от 3 тонн до 11 тонн. Данные экспериментов занесем в табл. 1.
Методом наименьших квадратов получим зависимости первого порядка натяжений S1 и S4 от деформаций Δ1 и Δ4:
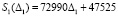 ;
;
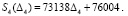 (12)
(12)
Полученные таким образом натяжения не являются реальными, так как имеет место ошибка аппроксимации. Но, имея эти зависимости, можно получить функцию Еμα(t) с незначительной погрешностью. Включим в модель блок, который будет вычислять натяжения по формулам (12), а затем и величину тягового фактора по формуле (10). Динамика тягового фактора представлена на рис. 4.
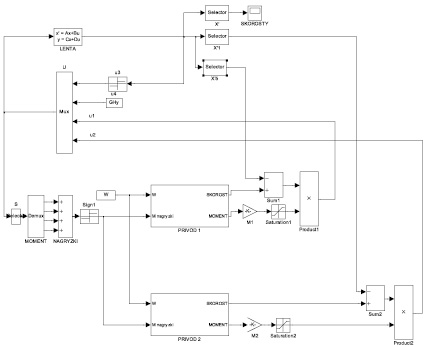
Рис. 2. Схема моделирования двухприводного конвейера в SIMULINK
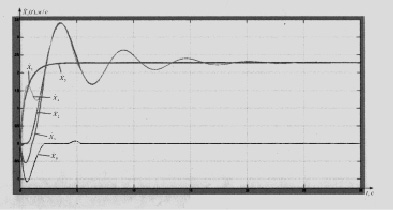
Рис. 3. Переходные процессы по скоростям обобщенных координат при пуске конвейера со скоростью 2,5 м/с
Таблица 1
|
Gну, Н |
Δ1, м |
Δ4, м |
S1, Н |
S4, Н |
|
30000 35000 40000 45000 52000 60000 70000 80000 90000 100000 110000 |
– 0,6298 – 0,5876 – 0,5482 – 0,5071 – 0,4488 – 0,3956 – 0,3289 – 0,268 – 0,2012 – 0,1377 – 0,07882 |
– 0,1337 – 0,09145 – 0,0521 – 0,01092 0,04753 0,1006 0,1672 0,2281 0,2949 0,3585 0,4173 |
2812,5 5312,5 7812,5 10312,5 13812,5 17812,5 22812,5 27812,5 32812,5 37812,5 42812,5 |
67500 70000 72500 75000 78500 82500 87500 92500 97500 102500 107500 |
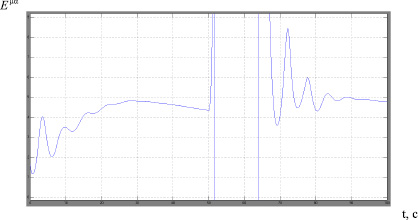
Рис. 4. Динамика тягового фактора без применения регулирования
Таблица 2
|
Gну, Н |
30000 |
35000 |
40000 |
45000 |
50000 |
52000 |
60000 |
70000 |
80000 |
90000 |
100000 |
|
s7 |
– 1,04 |
– 1,146 |
– 1,244 |
– 1,347 |
– 1,452 |
– 1,493 |
– 1,626 |
– 1,793 |
– 1,945 |
– 2,112 |
– 2,271 |
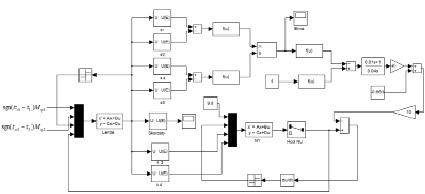
Рис. 5. Схема получения ошибки и осуществление регулирования положением каретки натяжного устройства
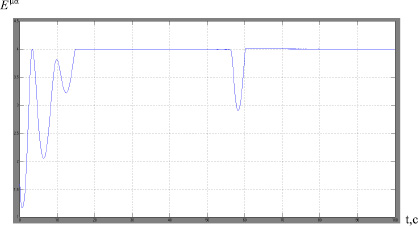
Рис. 6. Динамика тягового фактора при осуществлении регулирования положения каретки натяжного устройства
Видно, что при изменении скорости движения ленты происходят резкие колебания величины Еμα, причем его увеличение свидетельствует об увеличении натяжения грузовой ветви и уменьшении натяжения порожней ветви, следовательно, провисании ленты конвейера и пробуксовке. Для возможности регулирования Еμα определим зависимость между его величиной и весом натяжного устройства. Суть разрабатываемой системы стабилизации и будет заключаться в том, чтобы при переходе скорости движения ленты с одного уровня на другой изменять вес натяжного устройства, тем самым поддерживать тяговый фактор на заданном уровне. Зависимости Еμα(Gну) и обратная Gну(Еμα) найдены также методом наименьших квадратов с использованием Matlab Control System Toolbox. Используя обратную зависимость:
Gну(Еμα) = 250∙(Еμα)2 –
– 9980∙(Еμα)2 + 113380, (13)
можно вычислить разницу между желаемым значением тягового фактора и фактическим, т.е. ошибку. Полученная величина ошибки веса натяжного устройства может быть поставлена в соответствие ошибке перемещения каретки натяжного устройства s7. Эти данные приведены в табл. 2.
Наконец, была найдена зависимость между весом натяжного устройства и его перемещением. Эта зависимость имеет линейный вид:
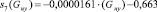 . (14)
. (14)
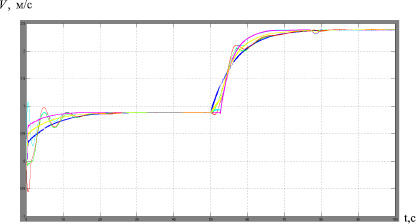
Рис. 7. Переходные процессы по скоростям сосредоточенных масс ленты конвейера при осуществлении регулирования
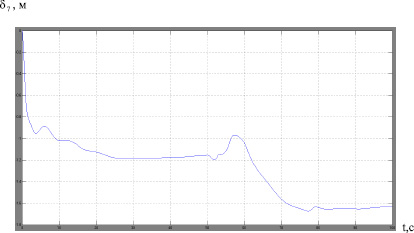
Рис. 8. Перемещение натяжного устройства при осуществлении регулирования
Выражение (8) динамики движения каретки натяжного устройства, т.е. координаты s7, можно положить в основу системы регулирования тягового фактора конвейера. Изменяя положение каретки натяжного устройство, можно изменять величину тягового фактора. Для этого выделим модель движения натяжного устройства из общей модели движения ленты конвейера (9) в отдельную систему, выходная величина которой (перемещение натяжного устройства s7) будет являться одним из внешних управляющих воздействий для модели ленты конвейера. Схема получения ошибки и осуществление регулирования тягового фактора путем изменения положения каретки натяжного устройства приведена на рис. 5.
При возникновении уже упоминавшейся ситуации, когда после повышения скорости вращения приводных барабанов натяжение на сбегающей ветви S1 сильно падает, в то время, как натяжение на набегающей ветви S4 возрастает, и величина тягового фактора выйдет за пределы желаемого уровня, каретка натяжного устройства изменяет свое положение, что позволяет избежать такого провисания ленты и пробуксовки. Результаты работы системы стабилизации приведены на рис. 6, 7, 8. Изменение положения каретки натяжного устройства происходит при переходе конвейера с одной скорости на другую и за счет этого изменения выбирается слабина ленты.
Как видно из графика на рис. 6, величина тягового фактора стабилизируется Еμα ≤ 4, что удовлетворяет требованиям беспробуксовочного движения ленты. На рис. 7 видно совместное плавное движение сосредоточенных масс ленты конвейера при движении с постоянной скоростью и при переходе конвейера на другую скорость. Можно сделать вывод об удовлетворительной работе системы стабилизации тягового фактора двухдвигательного конвейера.



