В современных инфокоммуникационных системах все большее применение находят параллельные вычислительные системы. Особенно наглядно это проявляется в системах цифровой обработки сигналов (ЦОС). Использование параллельных вычислений позволяет обеспечить реальный масштаб времени при обработке сигналов. Особое место среди систем ЦОС занимают цифровые фильтры (ЦФ). Реализация цифровых фильтров в модулярных кодах позволяет обеспечить максимальную производительность при реализации ЦОС. Кроме того, расширение числа оснований системы остаточных классов (СОК) позволяет обеспечить высокую точность обработки входного сигнала. Однако, при этом в значительной степени возрастают аппаратурные затраты на выполнение обратного преобразования из модулярного кода в позиционный код. Решить данную проблему можно за счет применения масштабирования результата, представленного в модулярном коде. Полученное при этом уменьшение числа рабочих оснований СОК позволит свести конечный результат к размерности входных данных, что положительно скажется на аппаратурных затратах, необходимых при обратном преобразовании с использованием китайской теоремы об остатках (КТО). Поэтому разработка алгоритма масштабирования модулярного кода является актуальной задачей.
Одной из самых динамичных и быстро развивающихся технологий в мире систем, комплексов и средств связи является цифровая обработка сигналов. Цифровая обработка сигналов – это технология, призванная решать задачи обработки сигналов в реальном времени с высоким качеством [1, 2, 4, 10]. Активное развитие средств ЦОС обусловлено, прежде всего, постоянным ростом требований к качеству обработки сигналов в системах связи и управления. Предпосылками к этому явилось совершенствование элементной базы вычислительных устройств, имеющее целью повышение производительности, точности вычислений и надежности устройств ЦОС.
Основным алгоритмом, реализующим ЦОС, является алгоритм цифровой фильтрации. Цифровая фильтрация в средствах связи используется в блоках предварительной обработки, представляющих собой блоки защиты от помех и в блоках цифровой обработки сигналов. В средствах связи цифровая фильтрация реализуется как традиционными цифровыми фильтрами, так и адаптивными цифровыми фильтрами, при этом традиционный цифровой фильтр является составным элементом адаптивного ЦФ [3, 4].
Все множество цифровых фильтров можно разбить на две большие группы:
– цифровые фильтры с конечной импульсной характеристикой (КИХ-фильтры);
– цифровые фильтры с бесконечной импульсной характеристикой (БИХ-фильтры).
Ввиду преимуществ КИХ-фильтров над БИХ-фильтрами, последние находят широкое применение в современных радиотехнических системах и системах связи [3, 8, 9]. Однако при практической реализации адаптивных систем, основой которых является КИХ-фильтр, разработчики сталкиваются со следующими проблемами:
– требуется большое время на вычисление выходного отсчета, поскольку алгоритм подстройки коэффициентов фильтра требует большого количества итераций;
– порядок фильтра составляет десятки-сотни отсчетов его импульсной характеристики, что определяет большие аппаратурные и энергетические затраты при его реализации на существующей элементной базе.
Одним из путей решения вышеуказанных проблем является реализация алгоритма цифровой фильтрации в алгебраической системе класса вычетов. На сегодняшний день имеется большое количество научных публикаций о преимуществах системы остаточных классов перед позиционной (двоичной) системой счисления в плане значительного повышения быстродействия, точности и отказоустойчивости работы устройств ЦОС, в том числе и ЦФ [2, 3, 10].
Математические основы построения СОК приведены в [5–8]. Используя естественные преимущества модулярных кодов перед позиционными кодами, возможно обеспечить повышение быстродействия, точности и отказоустойчивости работы ЦФ. Общая структурная схема ЦФ, функционирующего на основе системы остаточных классов, приведена на рис. 1 [6, 13–15]. Диапазон входных данных ЦФ будет определять количество вычислительных каналов фильтра и преобразователей данных из двоичного представления в модулярный код. В каждом вычислительном канале фильтра определение выходного отсчета осуществляется независимо, т.е. реализуется абсолютная параллельная обработка входных данных на уровне арифметических операций. Для представления выходных отсчетов фильтра в двоичном коде используется обратный преобразователь кода СОК в позиционный код.
При организации функционирования модулярного ЦФ необходимо обеспечить, чтобы диапазон представления данных в СОК Dсок был не меньше диапазона их представления в позиционном представлении Dпсс, т.е. должно выполняться следующее условие:
Dсок ≥ Dпсс , (1)
где Dпсс = 2n – n – разрядность входных данных ЦФ; Dсок = m1m2…mn + k, 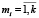 – основания СОК, которые должны быть взаимопростыми числами.
– основания СОК, которые должны быть взаимопростыми числами.
В статье приведены оценки для реализации модулярного цифрового фильтра, обрабатывающего 16-разрядные входные данные и 16-разрядные коэффициенты фильтра. Тогда диапазон входных данных составит Dпсс = 65536. Для выполнения условия, определяемого (1), выбран следующий набор оснований для упорядоченной СОК m1 = 2, m2 = 5, m3 = 7, m4 = 11, m5 = 13, m6 = 19.
Для обеспечения требуемой точности вычисления выходных отсчетов фильтра выбраны 16-разрядные коэффициенты. Следовательно, при выполнении операции умножения в вычислительном канале модулярного ЦФ результат должен быть 32-разрядный, т.к. операцию округления или усечения применять нельзя по причине того, что изменится представление промежуточного результата в СОК в каждом вычислительном канале и будет получен неправильный результирующий выходной отсчет фильтра. Учет этого обстоятельства потребовал выбора расширенной системы оснований, в которую включены основания:
mn + 1 = 23, mn + 2 = 29, mn + 3 = 31, mn + 4 = mn + k = 37.
Тогда расширенная система оснований СОК примет вид
m1 = 2, m2 = 5, m3 = 7, m4 = 11, m5 = 13, m6 = 19, m7 = 23, m8 = 29, m9 = 31, m10 = 37.
Так как импульсная характеристика ЦФ имеет отрицательные коэффициенты, то их представление в СОК осуществляется во второй половине диапазона Dсок (числа 32768 – 65535), в первой половине от 0 до 32767 осуществляется представление входных данных и коэффициентов ЦФ, имеющих положительный знак. Значение модуля m1 = 2 выбрано с точки зрения упрощения операции сравнения, полученного результата с величиной Dсок/2, т.е. определения области положительных или отрицательных чисел, в которую попал результат вычислений.
Увеличение количества оснований приводит к увеличению аппаратурных затрат. С целью их уменьшения предлагается провести масштабирование выходных отсчетов каждого вычислительного канала модулярного ЦФ. Операция масштабирования проводится путем деления полученного результата в каждом вычислительном канале на масштабирующий коэффициент Dм, который определяется как
Dм = mn + 1mm + 2mn + 3mn +4 . (2)
Проведение масштабирования приводит к значительному уменьшению аппаратурных затрат, ввиду того что преобразование выходных отсчетов модулярного ЦФ будет осуществляться не по 10 основаниям а по 6 основаниям: m1 = 2, m2 = 5, m3 = 7, m4 = 11, m5 = 13, m6 = 19.
Для проведения сравнительного анализа разработанного цифрового фильтра с масштабированием результата были созданы программные реализации позиционного и модулярного ЦФ, обрабатывающего 16-разрядные данные. Значения входных отсчетов ЦФ, снимаемых с выхода 16-разрядного АЦП, показаны на рис. 2.
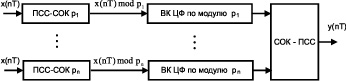
Рис. 1. Общая структурная схема ЦФ, функционирующего в системе остаточных классов
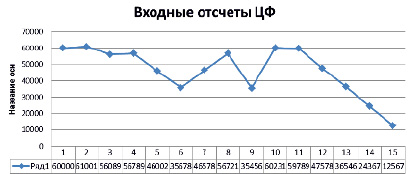
Рис. 2. Входные отсчеты цифрового КИХ фильтра, функционирующего в СОК
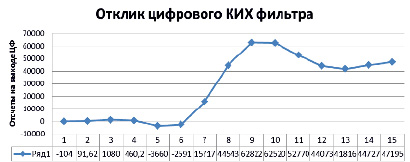
Рис. 3. Отклик позиционного цифрового КИХ фильтра
При использовании программной реализации позиционного цифрового фильтра был получен отклик, который показан на рис. 3.
При использовании программной реализации модулярного ЦФ без масштабирования были получены выходные 32-разрядные результаты, которые приведены в таблице.
Анализ таблицы показывает, что полученные отклики модулярного ЦФ совпадают со значением позиционного цифрового фильтра с коэффициентом масштабирования 105. Данное значение было выбрано с условием целочисленного предоставления коэффициентов КИХ фильтра 15 порядка.
При этом увеличение динамического диапазона фильтра привело к ситуации, когда для предоставления ортогональных базисов, которые используются для обратного преобразования из модулярного кода в позиционный код, требуется от 32 до 36 двоичных разрядов. Следовательно, перевод из кода СОК в код ПСС на основе китайской теоремы об остатках, с точки зрения схемных затрат, не является оптимальным.
Отклик цифрового КИХ фильтра, функционирующего в СОК
|
№ отсчета |
Значение |
№ отсчета |
Значение |
№ отсчета |
Значение |
|
Y(1T) |
– 10440000 |
Y(6T) |
– 259123121 |
Y(11T) |
5276991239 |
|
Y(2T) |
9125826 |
Y(7T) |
1571674266 |
Y(12T) |
4407237929 |
|
Y(3T) |
107929843 |
Y(8T) |
4454307516 |
Y(13T) |
4181550654 |
|
Y(4T) |
45960622 |
Y(9T) |
6282131308 |
Y(14T) |
4472603748 |
|
Y(5T) |
– 366015995 |
Y(10T) |
6251992481 |
Y(15T) |
4719415933 |
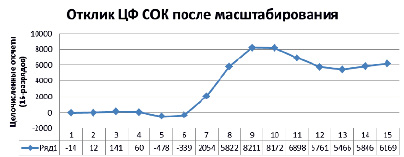
Рис. 4. Отклик ЦФ после масштабирования (данные приведены в ПСС)
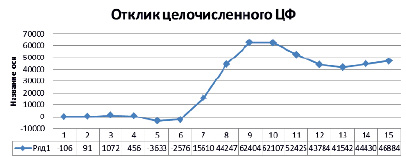
Рис. 5. Отклик целочисленного ЦФ СОК, использующего разработанный алгоритм масштабирования
Рассмотрим ситуацию, когда модулярный ЦФ использует разработанный алгоритм масштабирования. В этом случае коэффициент масштабирования будет определяться выражением (2) и для выбранной системы оснований СОК составит Dм = 765049. На рис. 4 приведен отклик ЦФ, функционирующего в СОК, после проведения масштабирования.
Так как в процессе вычисления выходного отсчета в вычислительных каналах модулярного ЦФ проводилась операция масштабирования, то после их преобразования из СОК в позиционную систему счисления необходимо провести умножение полученного результата на константу. Для обеспечения сходимости отмасштабированных результатов с откликом позиционного ЦФ необходимо полученные результаты умножить на коэффициент коррекции, который для данного КИХ-фильтра составляет Ккор = 7,652. Полученные результаты приведены на рис. 5.
Проведенные исследования показали, что применение разработанного алгоритма масштабирования позволило провести процедуру обратного преобразования из СОК в ПСС, используя 16-разрядные данные. Это позволяет сократить схемные затраты на операцию преобразования в 1,78 раза по сравнению с использованием КТО без проведения масштабирования результатов.
Выводы
Полученные результаты исследования позволяют сделать следующие выводы. Проведено обоснование целесообразности применения в ЦФ модулярных кодов. Для обеспечения обработки данных большой разрядности увеличивают число рабочих оснований СОК, что приводит к росту аппаратурных затрат на реализацию ЦФ. Особенно наглядно это проявляется при реализации обратного преобразования из модулярного кода в позиционный код. Для уменьшения диапазона представления данных в модулярных ЦФ и упрощения алгоритма обратного преобразования данных из СОК в позиционную систему счисления предложено провести масштабирование данных в вычислительных каналах фильтра. Использование разработанного алгоритма масштабирования в модулярном цифровом фильтре 15-го порядка, обрабатывающего 16-разрядные данные, позволило сократить аппаратурные затраты в 1,78 раза по сравнению с ЦФ СОК без масштабирования.



