На современном этапе развития к системам цифровой обработки сигналов (ЦОС) предъявляются высокие требования к быстродействию. Обеспечение реального масштаба времени позволит проводить ЦОС уже на первом этапе обработки. Это позволит повысить эффективность выполнения ортогональных преобразований сигналов, снизить схемные затраты, а также будет способствовать повышению точности выполняемых вычислений. Решить данную проблему можно за счет перехода к параллельным вычислениям.
Применение непозиционных параллельных модулярных кодов является одним из основных направлений, позволяющим решить проблему обеспечения выполнения алгоритмов ЦОС в реальном масштабе времени.
Среди множества алгоритмов ЦОС, реализованных с помощью непозиционных модулярных кодов, можно выделить две группы. Основу первой группы составляют методы и алгоритмы ортогональных преобразований сигналов с использованием системы остаточных классов (СОК) [1–3]. В этом случае цифровое преобразование входного вектора сигнала 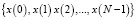 спектральное представление
спектральное представление 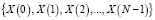 можно представить в виде выражения
можно представить в виде выражения
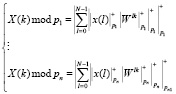 , (1)
, (1)
где Wlk – поворачивающий коэффициент; k = 0,1,2,…, N-1; N = 2v; p1, p2, …, pn – основания системы остаточных классов.
Анализ выражения (1) показывает, что к достоинствам системы остаточных классов можно отнести высокую производительность выполнения основных модульных операций, к которым относятся сложение, вычитание и умножение. Другими словами для двух чисел A = (α1, α2,…, αn) и B = (β1, β2,…, βn), справедливы равенства
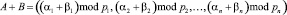 . (2)
. (2)
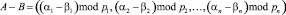 . (3)
. (3)
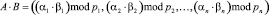 . (4)
. (4)
Основу второй группы непозиционных кодов, позволяющих эффективно реализовать алгоритмы цифровой обработки сигналов, являются коды полиномиальной системы классов вычетов (ПСКВ). Как показано в работах [4–6], использование ПСКВ позволяет не только повысить скорость выполнения алгоритмов, но и обеспечить высокую точность вычислений за счет обработки целочисленных данных. В этом случае выражение (1) будет представляться в следующем:
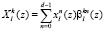 , (5)
, (5)
где 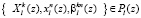 , l = 1, 2,…, m; k = 0,1,…d–1; βi(z) – первообразный элемент порядка d для локального кольца Pl(z); p1(z), p2(z),…, pl(z) неприводимые полиномы, порождающие кольцо Pl(z).
, l = 1, 2,…, m; k = 0,1,…d–1; βi(z) – первообразный элемент порядка d для локального кольца Pl(z); p1(z), p2(z),…, pl(z) неприводимые полиномы, порождающие кольцо Pl(z).
Данную математическую модель цифровой обработки сигналов (5) можно представить в виде системы уравнений:
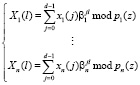 , (6)
, (6)
Как и ранее, вычисления алгоритмов цифровой обработки сигналов организуются параллельно, помодульно и независимо друг от друга. Другими словами, для суммы, разности и произведения двух полиномов A(z) и B(z), имеющих соответственно модулярные коды 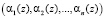 и
и 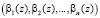 , справедливы соотношения при i = 1,…,n:
, справедливы соотношения при i = 1,…,n:
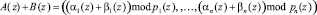 . (7)
. (7)
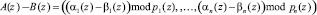 . (8)
. (8)
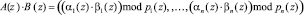 . (9)
. (9)
Анализ выражений (5) и (6) показывает, что одной из операций, которые используются в алгоритмах ЦОС, реализованных в кодах ПСКВ, является операция умножения по модулю. Поэтому разработка алгоритма и структуры умножителя по модулю, обладающего минимальными схемными затратами, является актуальной задачей.
В работах [7–9] приведен нейросетевой подход, позволяющий построить умножитель по модулю на основе нейросетевого базиса. Несмотря на то что нейронные сети, как и коды ПСКВ, обладают параллельной архитектурой, предложенный подход не позволил достичь минимальных схемных затрат не реализацию базовых модульных операций. В работе [10] предлагается снизить схемные затраты на реализацию модульных операций ПСКВ за счет применения генетического алгоритма. При этом использование мажоритарного генетического алгоритма с выделенной доминантой при обучении нейронной сети (НС), реализующей модульную операцию, не полностью позволило снизить затраты на реализацию НС. Это обусловлено тем, что в качестве синаптических весов в такой НС используются не только положительные значения.
Рассмотрим новый алгоритм реализации операции умножения по модулю. При проведении умножения по модулю 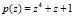 , двух операндов A(z) и B(z), степени которых удовлетворяют условию:
, двух операндов A(z) и B(z), степени которых удовлетворяют условию:
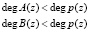 , (10)
, (10)
могут быть получены результаты, которые являются элементами поля Галуа GF(24). В табл. 1 приведены ненулевые элементы поля GF(24), порождаемые неприводимым полиномом 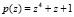 .
.
Так как операнды A(z) и B(z) представляют собой четырехразрядные комбинации, то максимальная степень их полиномиальной формы записи будет равна трем. Поэтому необходимо определить результаты каждого разряда первого операнда A(z) на каждый разряд операнда B(z). Пусть полином A(z) последовательно принимает значения 1, z, z2, z3. Результаты умножения A(z)B(z) по модулю 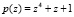 приведены в табл. 2.
приведены в табл. 2.
Обобщая данные, приведенные в табл. 2, можно определить, какие разряды операндов A(z) и B(z) участвуют в получении каждого разряда произведения 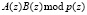 . Результаты приведены в табл. 3.
. Результаты приведены в табл. 3.
Рассмотрим первую строку табл. 3. Для того чтобы получить произведение 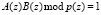 , при условии, что операнд A(z) = 1, необходимо условие, что B(z) = 1. Таким образом, для выполнения операции умножения по модулю для данных разрядов операндов достаточно использовать двухвходовой элемент И. Аналогичный результат получается для строки 2, 3, 4, 5, 9, 10, 13, 14, 15 табл. 3.
, при условии, что операнд A(z) = 1, необходимо условие, что B(z) = 1. Таким образом, для выполнения операции умножения по модулю для данных разрядов операндов достаточно использовать двухвходовой элемент И. Аналогичный результат получается для строки 2, 3, 4, 5, 9, 10, 13, 14, 15 табл. 3.
Рассмотрим шестую строку табл. 3. Для того чтобы получить значения произведения 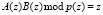 при условии, что первый операнд A(z) = z, значение второго операнда A(z) = z может быть 1 или z3. Это обусловлено равенствами
при условии, что первый операнд A(z) = z, значение второго операнда A(z) = z может быть 1 или z3. Это обусловлено равенствами
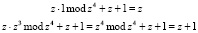 ,
,
в произведениях которых присутствует значение z.
Если одновременно подать единичный сигнал на разряды 1 и z3 второго операнда B(z), при условии, что A(z) = z, то получаем результат:
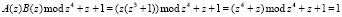 .
.
Этот результат получается, если сложить результаты двух произведений по модулю два
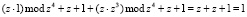 .
.
Таблица 1
Элементы мультипликативной группы конечного поля GF(24)
|
Степень элемента |
Полиномиальная форма |
Двоичный код |
Степень элемента |
Полиномиальная форма |
Двоичный код |
|
β0 |
1 |
0001 |
β8 |
z2 + 1 |
0101 |
|
β1 |
z |
0010 |
β9 |
z3 + z |
1010 |
|
β2 |
z2 |
0100 |
β10 |
z2 + z + 1 |
0111 |
|
β3 |
z3 |
1000 |
β11 |
z3 + z2 + z |
1110 |
|
β4 |
z + 1 |
0011 |
β12 |
z3 + z2 + z + 1 |
1111 |
|
β5 |
z2 + z |
0110 |
β13 |
z3 + z2 + 1 |
1101 |
|
β6 |
z3 + z2 |
1100 |
β14 |
z3 + 1 |
1001 |
|
β7 |
z3 + z1 |
1011 |
Таблица 2
Результаты умножения  .
.
|
A(z) |
B(z) |
|
|
1 |
1 |
1 |
|
z |
z |
|
|
z2 |
z2 |
|
|
z3 |
z3 |
|
|
z |
1 |
z |
|
z |
z2 |
|
|
z2 |
z3 |
|
|
z3 |
z + 1 |
|
|
z2 |
1 |
z2 |
|
z |
z3 |
|
|
z2 |
z + 1 |
|
|
z3 |
z2+ z |
|
|
z3 |
1 |
z3 |
|
z |
z + 1 |
|
|
z2 |
z2 + z |
|
|
z3 |
z3 + z2 |
Таблица 3
Результаты произведения 
|
№ п/п |
Разряды |
||
|
|
A(z) |
B(z) |
|
|
1 |
1 |
1 |
1 |
|
2 |
1 |
z |
z3 |
|
3 |
1 |
z2 |
z2 |
|
4 |
1 |
z3 |
z |
|
5 |
z |
1 |
z |
|
6 |
z |
z |
1, z3 |
|
7 |
z |
z2 |
z2, z3 |
|
8 |
z |
z3 |
z, z2 |
|
9 |
z2 |
1 |
z2 |
|
10 |
z2 |
z |
z |
|
11 |
z2 |
z2 |
1, z3 |
|
12 |
z2 |
z3 |
z2, z3 |
|
13 |
z3 |
1 |
z3 |
|
14 |
z3 |
z |
z2 |
|
15 |
z3 |
z2 |
z |
|
16 |
z3 |
z3 |
1, z3 |

Структура умножителя по модулю 
Значит, чтобы решить данную проблему, необходимо использовать двухвходовой сумматор по модулю два, на входы которого подаются сигналы с 1 и z3 второго операнда B(z). Выход этого сумматора по модулю два подключается на второй вход элемента И, на первый вход которого поступает сигнал в разряде z первого операнда A(z). Аналогичный результат получается для строк 6, 7, 8, 11, 12, 16 табл. 3. На рисунке приведена структура умножителя по модулю.
Умножитель содержит входы 1–4, на которые поступает в двоичном коде первый операнд A(z), входы 5–8, на которые подается двоичный код второго операнда B(z), блок двухвходовых сумматоров по модулю два 9.1–9.6, блок двухвходовых элементов И 10.1–10.16, сумматоры по модулю два 11–14, выходы которых являются выходом умножителя по модулю. При этом младшие разряды «1» первого и второго операндов A(z) и B(z) поступают на входы 1 и 5 соответственно, а старший разряд z3 – соответственно на входы 4 и 8. Выход сумматора по модулю два 11 соответствует младшему разряду произведения, а выход сумматора по модулю два 14 – старшему разряду произведения 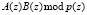 .
.
Рассмотрим работу умножителя по модулю. Пусть 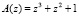 и
и 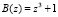 . Тогда их произведение по модулю
. Тогда их произведение по модулю 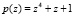 равно
равно
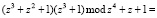
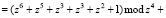
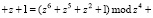
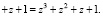
Следовательно, единичные сигналы должны появиться на выходах всех сумматоров по модулю два 11–14.
Рассмотрим работу схемы. В соответствии с выбранными значениями A(z) и B(z) единичный сигнал будет на входах 1, 3, 4, 5, 8 умножителей по модулю, а на остальных – нулевой сигнал. Тогда на выходах сумматоров по модулю два 9.2 и 9.5 будут получены единичные сигналы, а на всех остальных – нули.
Так как на 1 и 1 входы умножителя поступили единичные сигналы, то на выходе двухвходового элемента И 10.1 появится единичный сигнал. Так как на 1 и 8 входы умножителя поступили единичные сигналы, то на выходе двухвходового элемента И 10.4 также появится единичный сигнал. Так как на входы элемента И 10.10 поданы единичные сигналы с выхода элемента 9.2 и входа 3, то на его выходе также будет единичный сигнал. При этом т.к. на входы элемента И 10.15 поданы единичные сигналы с выхода элемента 9.5 и входа 4, то на его выходе также будет единичный сигнал.
Единичный сигнал с выходов элементов 10.1, 10.4, 10.10, 10.15 подается на соответствующие входы сумматоров по модулю два 11–14. В результате на выходах этих сумматоров появятся единичные сигналы. Полученные данные совпали с контрольным просчетом.
Выводы
Применение непозиционных модулярных кодов позволяет повысить скорость выполнения ортогональных преобразований сигналов. При этом наблюдается ситуация, когда происходит возрастание схемных затрат, необходимых для построения спецпроцессоров ЦОС. В работе предложен алгоритм выполнения операции по модулю, а также его схемная реализация. Использование данного умножителя позволяет обеспечить высокую скорость выполнения операции умножения по модулю при меньших схемных затратах.





