Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

В пространстве L2(Ω) (Ω – ограниченная область в Rn) рассмотрим краевую задачу

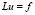в Ω,

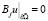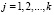, . (1)

Здесь 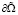– часть границы ∂Ω области Ω, L – необязательно линейный, а Bj(j = 1,2,3,…n) линейные дифференциальные операторы. Если в этом есть необходимость, пользуясь продолжениями из Ω на Rn, будем считать, что операторы L(∙) и Bj(∙)(j = 0,1,2,…n) определены для всех u из .

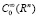Пусть Q – область, содержащая Ω. Предположим, что:

(П 1). Задача (1) для любого f∈L2(Ω) однозначно разрешима. Существуют область Q, содержащая Ω, и ограниченный интегральный оператор А, такие, что решение u задачи допускает продолжение из Ω на Q, представимое в виде

,

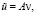
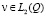причем

.

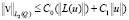(П 2). Операторы BjA(j = 1,2,3,…k) – ограниченные интегральные операторы в L2(Q), а преобразование L(Av) непрерывно.

Пусть g1, g2,… gn – функции, ограниченные на ∂Ω. Допустим, S – линейный оператор продолжения, сопоставляющий g1, g2,… gn – функцию u из L2(Q), такую, что в смысле обобщенных функций на ∂Ω выполнены равенства

, .

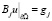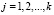Для функции 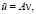определим

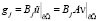
Продолжив эти gj(j = 1,2,3,…n) оператором S, получим

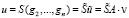. (2)

Для разности

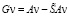. (3)

В смысле обобщенных функций имеем

, .

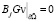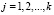Будем еще предполагать, что выполнено условие.

(П 3). Решения u задачи (1) представимы в виде

,

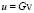при этом

.

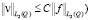Если выполнены предположения (П 1), (П 2) и (П 3), то в качестве В [1] можно взять единичный оператор, а в качестве А – оператор G из равенства (2). Тогда при некоторых условиях на G мы сможем воспользоваться результатами П 1. Оператор продолжения эффективно построить удается не всегда. Этот вопрос следует рассматривать отдельно в каждом конкретном случае.

Если оператор А удается выбрать удачно, то итерационная схема, составленная по алгоритму из [1], будет сходиться со скоростью геометрической прогрессии. Сложность выбора оператора А вызвана тем, что он связан граничными условиями. Построение оператора продолжения из П 3 является сложной технической задачей. Ниже мы предлагаем «грубый метод», который, на наш взгляд, более удобен в реализации.

Рассмотрим в области Ω∈Rn краевую задачу

,

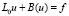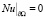. (4)

Здесь L0 – строго эллиптический оператор второго порядка, B(∙) – нелинейный оператор, N – линейный дифференциальный граничный оператор, не выше первого порядка.

(П 4). Предположим, что при любом f ∈L2(Ω) задача (4) имеет единственное решение u, которое продолжается на все Rn, так, что 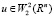и кроме того, если f ∈C(Ω), то gradu∈C(Ω).

Линейные операторы L0 и N (являющиеся, вообще говоря, операторами с переменными коэффициентами) также будем считать определенными на всех функциях из 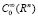. Будем предпологать, что B(u) = F(u, x), где F(∙,∙) – дважды непрерывно дифференцируемая функция своих аргументов u∈(– ∞, ∞), x∈Rn.

Нас интересует приближенное решение (4) при f ∈C(Ω). Согласно (П 4) решение задачи (4) ограничено. Ограничены также его первые производные. Поэтому решение (4) совпадает с решением следующей задачи:

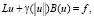(4’)

.

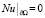Здесь γ(x) – дважды гладкая функция, такая, что

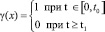, (5)

где t0 и t1 зависят от f0 и 0 < t0 < t1. Возьмем область Q, строго содержащую Ω. Тогда в силу (4) решение можно представить в виде u = Av, где A – самосопряженный интегральный оператор, действующий из L2 в :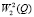

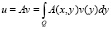, (6)

где .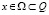

За ядро A(x, y) оператора A из (6) можно взять, например, функцию Грина для – Δ + E с периодическими краевыми условиями в кубе Q, содержащем в Ω. За A(x, y) можно также взять функцию Грина задачи Дирихле (или Неймана) для – Δ + E.

Еще один вариант выбора A(x, y) следующий. Пусть G(x – y) функция Грина оператора – Δ + E на всем Rn. Эта функция может быть выписана явно (ядро Бесселя-Макдонольда). Положим A(x, y) = χQ(x) G(x – y) χQ(y), где χQ(∙) – характеристическая функция области Q, а Q – произвольная область, содержащая Ω (в частности, Q может совпадать со всем Rn). Подставим u = Av в уравнение (6) и получим

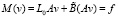в Ω,

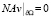. (7)

Здесь 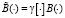. Введем функционал

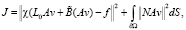
где DS – элемент поверхности ∂Ω. Оператор NA будет интегральным, с ядром N(x, y).

Поэтому, как и в [1], J можно записать в виде

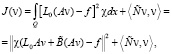(8)

где χ – характеристическая функция Ω, 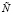– самосопряженный интегральный оператор с ядром

.

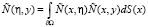Если v – решение задачи (7), то J обращается в нуль и наоборот, если J(v) = 0, то v есть по крайней мере или слабое, или обобщенное решение задачи (7). Следовательно, приближенное решение (7) можно искать как последовательность, реализующую минимум J.

Для минимизации J(v)нужны некоторые предположения.

(П 5). Существует θ∈[0,1], такое, что, если J(v1), J(v2) < C < ∞ то χAv1, χAv2 имеют продолжения u1 и u2 из Ω на Q, для которых

,

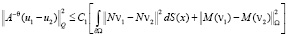где C1 – не зависит от v1 и v2. Это предположение для корректных эллиптических задач, как правило, выполняется, при этом θ < 1.

Норма левой части тем сильнее, чем больше θ. Увеличению θ мешает в основном граничное условие.

(П 6). Если 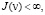то 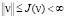, а задача

,

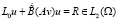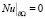
однозначно разрешима. Причем u допускает продолжение 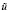из Ω на Q, удовлетворяющее оценке

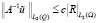
где c не зависит от R, но может зависеть от J(v).

Сначала рассмотрим «дифференциальный» вариант приближенного решения задачи (4). Допустим, что v в выражении для J зависит от параметра ξ. Продифференцируем J по ξ:

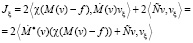
Здесь

,

.

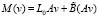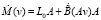Выберем vξ из уравнения

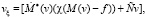
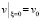. (9)

Нетрудно доказать, что задача Коши разрешима. Таким образом,

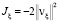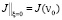, . (10)

Отсюда вытекает

,

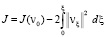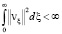. (11)

В предположении (П6) за R примем χ(M(v) – f). Пусть 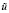– функция из (П6). Умножим vξ скалярно на 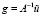. Тогда

.

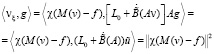(Здесь мы учитывали, что 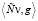обращается в нуль в силу равенств )

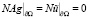Из (П6) и полученного для 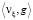равенства имеем

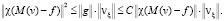
Отсюда и из (11) вытекает, что

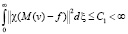(12)

Умножим теперь vξ на v скалярно и проинтегрируем от 0 до ξ:

.

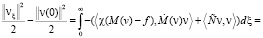
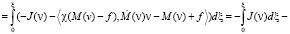
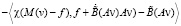Это равенство и (12) дают оценку

.

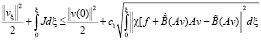В силу построения 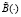подынтегральное выражение в правой части ограничено постоянным числом. Поэтому

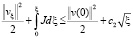. (13)

Далее из (11) получаем, что J по ξ монотонно не возрастает. Следовательно (14), вытекает

.

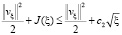А это неравенство дает

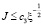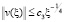, . (14)

Теперь воспользуемся предположением (П 2). Тогда получаем, что имеет место

Теорема 1. Пусть выполнены предположения (П 5), (П 6) и (П 7). Тогда, если v решение  (9). Положим u = Av, тогда имеет место оценка

.

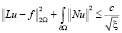Доказательство. Первое неравенство непосредственно следует из (13). Достаточно доказать второе неравенство. Из предположения (П6) имеем

.

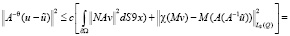
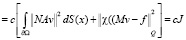Отсюда вытекает второе неравенство теоремы.

Замечание 1 . В условиях теоремы 1 при ξ → ∞ функционал J стремится к нулю, а v стремится к решению. Стремления к нулю J можно добиться в более слабых ограничениях. Например, возьмем

,

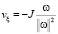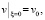
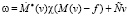. (14)

Подставляя vξ в выражение для Jξ, получаем Jξ = – J. Поэтому при таком выборе vξ

,

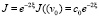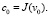
Видно, что J стремится к нулю экспоненциально. Но отметим, что задачу Коши (14) теперь труднее решать (а также доказывать существование ее решения), чем задачу (9).

Выкладки этого замечания верны для очень обширного класса задач, по крайней мере, формально. Поэтому, базируясь на выборе (14), можно составить для задачи (14) (а следовательно, и для (7)) итерационный процесс

,

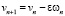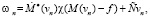
n = 1,2,…. (15)

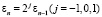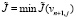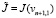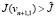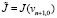В этом процессе ε1,ε2…, выбирается следующим образом. Пусть уже выбран εn – 1. Вычислим vn + 1 по формуле (10). Выбрав и обозначив вычисленное значение vn + 1 через vn + 1,j), найдем J(vn + 1,j) (j = – 1,0,1). Обозначим (j = – 1,0,1). Если , то берем εn = 2εn – 1, если же и , то берем εn = εn – 1.

Наконец, если J(vn + 1,1), 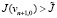, то берем 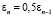. Мы можем оказаться в ситуации, когда вычисленное значение J(vn + 1) (с уже выбранным) εn не меньше, чем J(vn). В таком случае нужно делать пересчет vn + 1, взяв εn = 0,5εn. Для достаточно общих краевых задач, которые удовлетворяют (П 4), (П 5) и (П 6) можно доказать, что такой расчет приведет к построению последовательности vn, для которой имеет место соотношение J(vn) → 0. В предположениях (П 5), (П 6) из стремления J(vn) к нулю вытекает сходимость vn (в слабой метрике) к решению задачи (7).

Основным недостатком метода, описанного выше, является тот факт, что уравнение  (9), позволяющее строить приближенное решение (7), само есть дифференциальное уравнение. Более удобным для численной реализации был бы дискретный вариант (14).

Считаем также, что выполнены предположения (П 4), (П 5) и (П 6). Кроме того, предположим также, что выполнено следующее условие.

(П7). Если 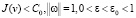, то выполнено неравенство 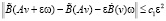, где c1 < ∞ непрерывно зависит от c0 и не убывает при возрастании c0.

Пусть 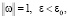где ε0 – число, фигурирующее в (П 7). Тогда

=

+

.

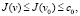
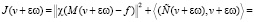
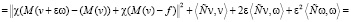
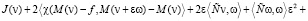
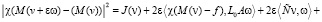
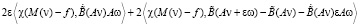
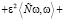
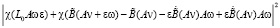Отсюда и из предположения (П 7) вытекает, что

,

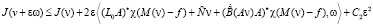где C2 зависит от J(v0) =C0. Выберем 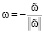, где

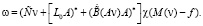
Откуда

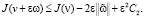(16)

Оценим 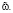Пусть g – решение задачи

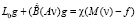в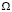

.

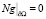Продолжим g с Ω на Q согласно (П 6). Это продолжение обозначим также через g. Положим 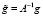. Умножим ω скалярно на g. Тогда с учетом граничного условия на g, определения Т и выбора g, имеем

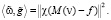
Теперь, учитывая (4.3), получаем

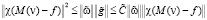
Поэтому

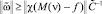. (17)

Отсюда вытекает, что 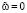, если J(v) ≠ 0. Действительно, если 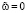, то из (17) следует, что 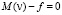в Ω. Поэтому в силу определения 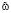имеем 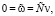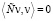. Но тогда J(v) = 0. В случае J(v) = 0 получаем, что v – решение (7), и цель достигнута. Следовательно, можно считать, что 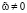. Выберем теперь ε положительным и таким, что 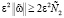. Отсюда и из (16) вытекает

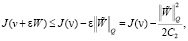
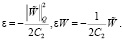(18)

Определим последовательность 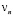по рекуррентным формулам:

,

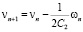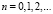
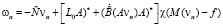(19)

(напомним, что χ – характеристическая функция Ω).

Теорема 2. Пусть выполнены предположения (П 4), (П 5), (П 6), (П 7) и пусть vn(n = 0,1,2,…) – последовательность, построенная по рекуррентным формулам (15). Тогда

,

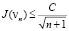где С не зависит от f.

Функции χAvn имеют продолжения 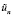из Ω на Q, такие, что

().

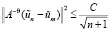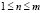Последовательность Avn сходится к решению задачи (4).

Доказательство. Из (14) вытекает, что

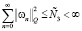. (20)

Умножим ωn на vn скалярно

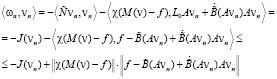
или

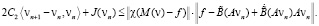
Просуммируем эти неравенства по всем n от 0 до k:

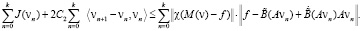
Теперь воспользуемся (12), (14) и построением 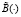по B(∙). Получим неравенство

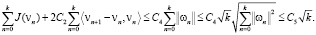(21)

Преобразуем второе слагаемое левой части последнего неравенства (16):

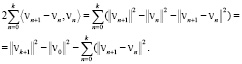
Отсюда, учитывая соотношение

,

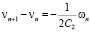из (16) имеем оценку

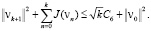
Поскольку функционал J(vn) не возрастает по n, из этого неравенства следует оценка

.

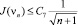Это неравенство и предположение (П 6) доказывают теорему.

О приближенном решении нелинейной параболической задачи

Рассмотрим задачу

,

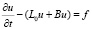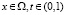
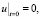
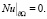(22)

Здесь L0 – строго эллиптический линейный оператор второго порядка, 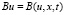– дважды непрерывно-дифференцируемая функция своих аргументов , , .

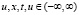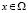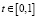Если для задачи

,

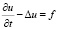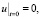
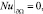(23)

можно явно написать функцию Грина, то использование результатов из [1] дает эффективный метод решения.

Как правило, для задачи (23) явно выписать функцию Грина невозможно. Поэтому мы будем действовать методом, описанным выше, т.е. методом фиктивных областей.

Пусть Q – куб, содержащий Ω. Помимо (17) рассмотрим задачу

,

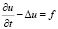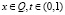
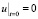(24)

По пространственным переменным присоединим к (24) периодические краевые условия.

Пусть 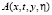– функция Грина задачи (24). Она может быть выписана явно. Обозначим

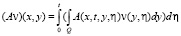. (25)

Приближенное решение задачи (23) будем искать в виде 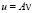. Тогда v, очевидно, удовлетворяет уравнению

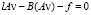, (26)

где .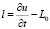

Для Av начальное условие

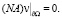(27)

Так же, как и в [1], имеются другие варианты выбора А, например,

,

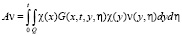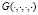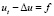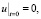
где – функция Грина для уравнения теплопроводности , 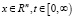. Явный вид 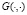можно найти в любой книге по уравнениям математической физики.

Для приближенного решения задачи (22) будем пользоваться следующими предположениями (П 8), (П 9), (П 10):

(П 8). Задача (22) однозначно разрешима для любого 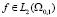, где 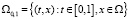. Причем, если 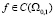, то решение u(t, x) также непрерывно на Ω0,1.

В силу этого предположения при 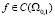решение (22) совпадает с решением

,

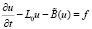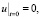
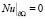, (28)

где 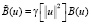. Здесь γ должна быть непрерывно дифференцируемой функцией, которая равна 1 при 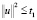и нулю при 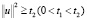. Числа t1 и t2 зависят от f. Будем решать задачу при .

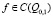Теперь вместо (26)–(27) имеем

,

.

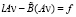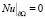Введем, как обычно, функционал J(v):

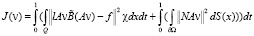
(dS(x) – элемент поверхности 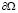, χ – характеристическая функция Ω). Как и в [1], этот функционал можно переписать в виде

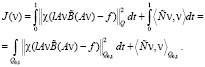
Здесь 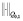и 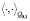норма и скалярное произведение в ,

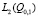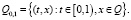
Теперь можем перечислить остальные предположения, которые нужны в дальнейшем.

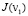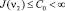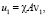
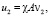(П 9). Если , и то

.

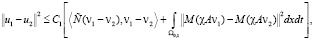
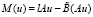(П 10). Если 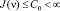, то задача

, ,

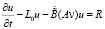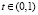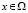
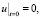
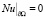
однозначно разрешима, причем решение u(t, x) из Ω0,1 продолжается на Q0,1 так, что

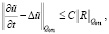
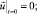
по пространственным переменным функция 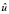( 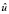– продолжение u) удовлетворяет периодическим краевым условиям.

(П 11). Если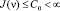

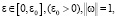
то

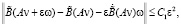
где 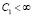непрерывно зависит от C0 и монотонно не возрастает при возрастании C0.

Построим последовательность vn по рекуррентным формулам

.

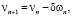
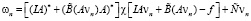Так же, как аналогичная выше, доказывается теорема.

Теорема 3. Пусть f непрерывна Ω0,1 и выполнены предположения (П8) – (П11). Существует число δ0 > 0, такое, что при 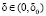последовательность, построенная по формулам (6.6), удовлетворяет условиям:

1) J(vn) монотонно убывает и стремится к нулю, причем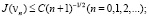

2) χAvn стремится в 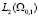к решению u задачи (3.81), причем

.

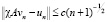Так как точное значение δ из теоремы найти трудно, целесообразно поступить следующим образом: нужно взять δ не постоянным, а зависящим от m. Пусть δm на m-м шаге уже принята. Подсчитаем vm + 1 и J(vm + 1) с δm + 1, равной δm, а затем подсчитаем 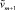и 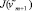, положив δm + 1 = δm. Если 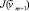≤ J(vm + 1), то окончательно примем δm + 1 = δm, J(vm + 1) ≤ 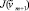, то за δm + 1 возьмем 0,5δm.