Известно, что законы классической механики, также как и законы любой другой области физики имеют свою определенную область применения, границу этой области, естественно классическая механика представляет собой частный случай более общей квантовой механики.С развитием квантовой механики в начале двадцатого века полностью все законы теплового излучения нашли свое теоретическое подтверждение.Именно квантовая механика возникшее в 1900 году обьяснила спектр излучения абсолютно черного тела, законы теплового излучения (закон Стефана-Больцмана, закон Рэлея-Джинса, законы Кирхгофа, закон смещения Вина и т.д.), а современная физика опирается в основном на квантовую механику. При описании законов природы в микромире квантовая механика представляет ее волновой теорией вещества и обязательно включает в нее h = 6,62× ×10–34 Дж×с, постоянную Планка [1, 2].
По предположению Планка осциллятор излучает свет отдельными порциями с энергией Е = hν. Именно на достижения и успехи квантовой механики опирается вся современная физика. В основе квантовой механики лежит соотношение де Бройля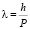 
. Именно вот это соотношение показывает точную взаимосвязь корпускулярной и волновой природы микрочастицы. После соотношения де Бройля стало ясно, что двойственная природа присуща не только для света но и для любой микрочастицы.
Здесь нам хотелось бы отметить такое обстоятельство, что при изучении законов микромира в обязательном порядке нужно хорошо усвоить следующие принципиальные вопросы, которые сильно отличаются от законов классической механики:
1. Соотношение неопределенности Гейзенберга.
2. Корпускулярно-волновой дуализм.
3. Квантовая теория атома водорода.
Основной характерной особенностью микромира, тесно связанной с исследованиями законов природы микромира является принцип неопределенности Гейзенберга. Этот принцип утверждает, что имеются пары величин, характеризующие микроскопическую систему, которые не могут быть известны одновременно с бесконечной точностью. Например, рассмотрим, электрон. Его координата, и импульс определяются с некоторой точностью. Тогда для определения местоположения (координаты) и импульса микрочастицы существует следующее соотношение, которое называется соотношением неопределенности Гейзенберга:
,
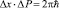где һ – постоянная Планка.Если оказывается, что местоположение известно с высокой точностью, то из принципа неопределенности следует, что мы ничего не знаем о значении импульса и наоборот.Такое же соотношение, получаем для энергии и времени, связанных с некоторым данным событием или состоянием:
.
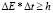Принцип неопределенности является следствием того факта, что мы представляем частицу в виде волнового пакета, в котором бесконечно большое число N монохроматических волн, образующих пакет,имеет некоторый разброс по частоте. Частица находится где-то в области Δх внутри пакета и неточность определения импульса равна Δр.
Нужно отметить, что именно после развития квантовой механики это соотношение неопределенности Гейзенберга была блестяще доказана теоретическим путем в ходе рассмотрения волнового пакета [1, 3].
Эта неточность свойственна самой природе систем, которые мы рассматриваем, и является отражением того предела, которого достигли наши знания о микромире. Всегда следует помнить, что определение координаты, импульса и других характеристик микрочастицы производится непосредственно при помощи определенных конкретных приборов, а эти приборы сами состоят из этих микрочастиц, значит эта неопределенность уже заложена самой природой в этих приборах. Более точнее определить координату и импульс микрочастицы невозможно, сама постоянная Планка – это тридцать четыре знака после запятой,показывает предел наших возможностей. Эта неточность не имеет ничего общего с какими бы то ни было техническими трудностями, возникающими в настоящее время при конструировании более точных измерительных приборов.
В данном случае непременно нужно отметить следующий очень существенный момент, который немного поясняет соотношение неопределенности Гейзенберга. Взаимодействие между микрочастицами и макроскопическими телами, разумеется, существенно отличается от взаимодействия макроскопических тел между собой.Именно, при взаимодействии между одним микроскопическим телом и другим, играющим роль прибора, всегда можно считать обратное воздействие прибора на тело как угодно малым или, хотя бы, точно учесть его. Поэтому говорят, что воздействие прибора не изменяет состояние макроскопического обьекта.
Иначе дело обстоит при взаимодействии физических обьектов разной природы – микрочастицы и макроскопического тела – прибора. Здесь принципиально невозможно считать воздействие на микрочастицу малым и несущественным. Вот этот существенный момент показывает, что воздействие прибора на электрон изменяет его состояние и при этом принципиально не может быть сделано малым. Поэтому мы получаем неопределенность значений координаты и импульса микрочастицы. Мы можем лишь найти вероятность того или иного значения этих величин.
Данная неопределенность координаты и импульса накладывает абсолютные ограничения на принципиально достижимую точность многих измерений [3, 4].
Теперь рассмотрим второй вопрос корпускулярно-волновой дуализм, который имеет не менее важное значение. Известно, что свет представляет собой двойственную природу, в одних явлениях она ведет себя как волна, в других явлениях она ведет себя как частица.
В квантовой механике частицу массой m, импульсом р, и полной энергией Е представляют как волновой пакет. По аналогии с материальным обьектом, микрочастицу можно представить в виде волн. Тот факт, что частица ассоцируется с волной, ставит вопрос о том, как поступить со свойством занимать в определенный момент определенное место в пространстве. Система волн, суперпозиция которых дает огибающую, оно распространяется со скоростью, отличной от скорости составляющих волн. Эту огибающую волн, которая рассматривается как материальная частица, называют волновым пакетом.(или группой волн). Здесь следует отметить, что скорость частицы будет равна в точности групповой скорости волн де Бройля. В принципе групповая скорость фотонов будет равна скорости самого фотона [4].
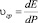, v = с
Вот здесь естественно возникает вопрос: «С чем мы имеем дело, может эта частица с определенной массой, импульсом и энергией, или же это волна с определенной амплитудой, частотой и длиной волны?» Очевиден ответ: частица –волна обладает двойственной природой. В квантовой механике электрон рассматривается – как микрочастица, со свойственными специфическими свойствами, иногда она проявляет свои волновые характеристики, иногда она проявляет свои корпускулярные свойства. Как проявит данная частица свою волновую или корпускулярную природу, это зависит от способов наблюдения и от постановки задачи при проведении эксперимента. Проблема двойственности возникает во многом из-за слишком упрощенного характера наших математических расчетов. С применением более сложной квантовой теории поля эта проблема в значительной мере теряет свою значимость. [4].
Теперь попытаемся разобраться с квантовой теорией атома водорода. Здесь следует отметить, что развитие квантовой механики в начале двадцатого века на самом деле происходило лишь благодаря огромным титаническим усилиям многих крупнейших теоретиков и экспериментаторов того времени, это невероятно сложная теория современной физики и физики микромира. Мы не будем перечислять имена крупных ученых физиков того периода, но отметим что это был огромный колоссальный труд физиков двадцатого века [1, 2].
Теория Бора, хотя она имеет свои недостатки и преимущества, сыграла свою огромную роль в развитие начала квантовой механики, без этой теории трудно представить дальнейшее развитие физики микромира. Эта теория, отличавшаяся смелостью и простотой, дала ответы на многие вопросы,волновавшие физиков-экспериментатаров того времени. Однако, как оказалось, несмотря на первоначальный успех, эта теория не смогла удовлетворительно разрешить целый ряд проблем:
1. Почему переходы осуществляются именно между данными энергетическими уровнями, а не между какими-либо другими?
2. Почему электроны не излучают электромагнитную энергию и не падают по спирали на ядро ?
3. Какова природа спектров более сложных атомов, в частности гелия или лития ?
Теория Э. Шредингера, использовавшего понятия квантовой механики и волновых функций, была как бы завершаюшим шагом в создании теории строения атома, развитие тех идей, которые впервые высказал Н. Бор. Атом водорода с его самой простой внутренней структурой представляет собой очень хороший обьект для первоначального применения теории Шредингера. Успешные результаты, полученные при исследовании структуры спектра водорода, являются первыми большими достижениями квантовой механики. Не вдаваясь в сложные математические выкладки можно сказать, что теория Шредингера смогла решить задачи микромира, получить результаты, которые нельзя получить на основе теории Бора [3–4].
Квантовая механика позволила,в частности, решить проблему,связанную с вырождением энергетических уровней, а также уточнить атомную модель, приведя ее в лучшее соответствие со свойствами атомов, существующих в природе.