Вибрационные технологические процессы получили широкое распространение в производственных системах, относящихся к различным отраслям техники. Вибрации имеют существенное значение в процессах вибрационного перемещения, транспортировании объектов и рабочих сред, активно используются в технологиях обработки деталей [1, 2].
Цель исследования заключается в разработке математических моделей и критериев оценки форм движения с учетом влияния неудерживающих связей в динамических взаимодействиях элементов вибрационных технологических процессов в приложениях к задачам повышения надежности и эффективности работы вибрационных машин. В рамках обозначенной цели решается задача построения математических моделей динамических процессов взаимодействия обрабатываемых деталей и сыпучей среды с учетом особенностей, возникающих в процессе работы определенного типа вибростендов.
В соответствии с рис. 1 приводится кинематическая схема вибростенда, образованного тремя секциями, которые опираются на упругие элементы.
Момент вращения от двигателей передается на два вала с вибраторами. Синхронизаторы обеспечивают вращение валов в противоположных направлениях, что приводит к взаимному сокращению горизонтальных компонент силовых возмущений от вибраторов. Особенностью системы приводов является использование карданных передач (рис. 1, поз. 3), которые обеспечивают синхронное вращение каждого из двух валов с противовесами. Упругие элементы стенда представляют собой прорезиненные рукава.
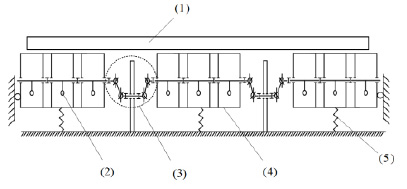
Рис. 1. Кинематическая схема вибростенда: 1 – контейнер с изделием; 2 – вибратор; 3 – карданные передачи между валами вибратора и валом синхронизатора; 4 – секция вибростенда; 5 – амортизатор
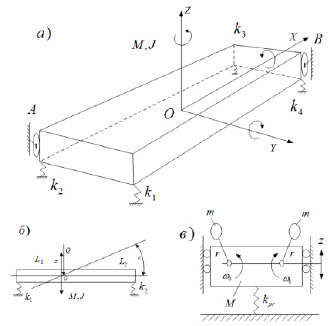
Рис. 2. Этапы формирования упрощенных моделей вибростенда: а – принципиальная схема упруго-инерциальной системы; б – упрощенная принципиальная расчетная схема вибростенда с двумя координатами z и j; в – схема вибростенда в реализации вертикальных колебаний
В силу конструктивно-технических ограничений и особенностей системы инерционного вибрационного возмущения колебаний, доминирующей формой является вертикальная (рис. 2).
Принципиальная схема упруго-инерционной системы приведена на рис. 2-а, дающем представление о пространственной структуре динамических взаимодействий рабочей среды с вибрирующей поверхностью детали. На рис. 2-б показана упрощенная расчетная схема, отражающая движение системы с двумя степенями свободы. Такая схема может рассматриваться в качестве основной, но и она может быть упрощена, как показала обработка экспериментальных данных, что было сделано на основе построения матрицы коэффициентов взаимной корреляции сигналов 6-ти датчиков, расположенных симметрично по периметру вибростола. Расчетная схема на рис. 2-в может рассматриваться как упрощенная расчетная схема вибростенда с доминантой вертикальных колебаний. Данные для обобщений были получены на основании экспериментальных измерений, которые проводились на вибрационной технологической машине. В составе измерительного комплекса использовалась сейсмическая станция BY-8 (Байкал-8). Для получения данных в соответствии с программой эксперимента 6 датчиков размещались на секции вибростенда (рис. 3) и синхронизаторе (рис. 4).

Рис. 3. Установка датчиков на секции вибростенда: 1, 2 – датчики

Рис. 4. Установка датчиков на синхронизатор вибростенда: 1, 2 – датчики из комплекта BY-8
По результатам серии производственных циклов упрочнения были произведены записи сигналов по синхронным 6 каналам.
В соответствии с рис. 5 представлена расчетная схема механической системы с учетом неудерживающего характера связей между телами с массами m1 и m2.
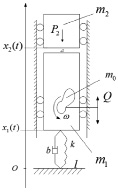
Рис. 5. Расчетная схема механической системы с учетом неудерживающего характера связей
В используемой на предварительном этапе абстрактной модели предполагается, что отрыв элементов составного твердого тела происходит в момент времени t0, для которого выполнены условия отрыва (условия отрыва и формируемые после отрыва траектории под действием силовых факторов рассмотрены в работах [3–7]). После отрыва тело с массой m2 движется под действием силы гравитации P2 до момента соударения.
Проведенные эксперименты показывают возможность возникновения форм самосинхронизации движения, в которых поведение сыпучей среды от жидкостно-подобного состояния трансформируется в стороны повышения «условной вязкости». Предлагаемый метод построения системы математических моделей, позволяющий строить определенные фрагменты, объединенные в обобщенный подход, основан на последовательном развитии принципа формирования определенных видов движений, создающих необходимые структуру и параметры вибрационного поля [8].
Такие образом, технологические машины, реализующие вибрационные процессы непрерывных и устойчивых взаимодействий с обрабатываемыми поверхностями деталей, должны создаваться с использованием и оценкой возможностей генерации доминирующих движений. На основе разработанного подхода предложена аналитическая модель процесса непрерывного подбрасывания типового элемента сыпучей среды, соударяющегося с обрабатываемой поверхностью. Как показывают проведенные исследования, условия непрерывного подбрасывания с фиксированной кратностью времени полета по отношению к периоду колебания опорной поверхности может стать основой для поиска устойчивых режимов и оценки таких режимов на предмет эффективности. Вместе с тем, переход к математическим моделям, отражающих свойства сыпучей среды, рассматриваемой в виде слоя, масса которого составляет 15 %–20 % от массы вибростола, требует учета двух основных факторов: влияния, возникающих при соударениях чередующихся импульсов, и рассеяние энергии при взаимных контактах взаимодействий шариков, образующих слой.



