Данная статья посвящена анализу одного из аспектов проблемы выбора признаков изображения для слежения за объектом. Существуют различные алгоритмы слежения (трекинга), оценивающие положение одного или нескольких объектов на кадрах видеопоследовательности, которые входят в многочисленные приложения компьютерного зрения в робототехнике и видеонаблюдении. Выбор подходящих признаков изображения может сыграть критическую роль при реализации алгоритмов трекинга. Очень важно правильно выделить характерную особенность изображения на ранних этапах реализации подобных методов, которая позволит объектам быть легко различимыми среди множества других [1].
Представим набор признаков изображения как: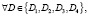 
де D1 – цветовая модель, D2 – оптический поток, D3 – границы, D4 – текстура.
Каждому признаку изображения соответствуют различные методы его нахождения:
– D1 = {dRGB, dHSV, dLuv, dLab}, где dRGB – цветовая модель RGB, dHSV – цветовая модель HSV, dLuv – цветовая модель Luv, dLab – цветовая модель Lab;
– D2 = {dLK, dHS, dF, dSF}, где dLK – определение оптического потока по методу Лукаса-Канаде (Lucas-Kanade), dHS – определение оптического потока по методу Хорна-Шанка (Horn-Schunck), dF – определение оптического потока по методу Фернебака (Farneback), dSF – определение оптического потока по методу SimpleFlow;
– D3 = {dCED}, где dCED – оператор обнаружения границ изображения Кэнни (Canny edge detector);
– D4 = {dGLCM, dLTEM, dw, dsp}, где dGLCM – матрицы сходимости GLCM (Gray-Level Cooccurrence Matrices), dLTEM.– двадцать 2D фильтро образованных из пяти 1D фильтров (Laws Texture Energy Measures), dw – вейвлет, dsp – управляемый фильтр (Steerable filter).
Аналитическая модель. В рамках анализа рассмотрим метод определения оптического потока, позволяющий вычислить, на сколько тот или иной объект сместился по отношению к его же положению на предыдущем кадре за то время, которое прошло между фиксацией кадров. Рассмотрим один из классических методов нахождения оптического потока – метод Лукаса-Канаде. Вычислительная сложность этого алгоритма – O(Nnm), где N – количество признаков, n – число уровней пирамиды, m – среднее число итераций. В основе классического метода Лукаса-Канаде лежит предположение, что значения интенсивностей пикселей не изменяются во времени:
I(x + u, y + v, t + 1) = I(x, y, t), (1)
где I(x, y, t) – функция интенсивности пикселя x = (x, y)T в кадре t и u = (u, v)T – смещение пикселя между последовательными кадрами t и t + 1. При малом смещении, линейное разложение в ряд Тейлора дает следующее уравнение оптического потока:
f(u, v; I) = Ixu + Iyv + It= 0, (2)
где индексы обозначают частные производные. При этом возникает проблема апертуры [3] из-за того, что этого одного уравнения (2) недостаточно для определения двух неизвестных u и v.
Метод Лукаса-Канаде [4] для решения этой проблемы предполагает, что неизвестное смещение пикселя u постоянно в пределах некоторой окрестности. В результате этого, смещение может быть вычислено путем минимизации:
ELK (u, v) = Kρ*((f(u, v; I))2), (3)
где Kρ * ( ∙ ) – свертка с окном интеграции размера ρ. После дифференциации уравнения по параметрам u и v и приравнивания частных производные к нулю, получаем следующую линейную систему:
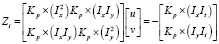(4)
Диаграмма алгоритма Лукаса-Канаде представлена на рисунке.
Алгоритм Лукаса-Канаде:
Для каждого признака i:
1. Инициализировать ui ← (0, 0)T
2. Задать λi ← 0
3. Для уровня пирамиды от n − 1 до 0 с шагом −1:
(a) Вычислить Zi (4)
(b) Повторить до сходимости:
I. Вычислить разницу It между первым изображением и смещенным вторым:
It (x, y) = I1 (x, y) − I2 (x + ui, y + vi)
II. Вычислить ei (3)
III. Решить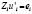 
для увеличивающегося движения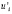 
IV. Добавить увеличивующееся движение для общей оценки: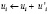 
c) Перейти на следующий уровень: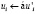 
где α – коэффициент масштабирования пирамиды
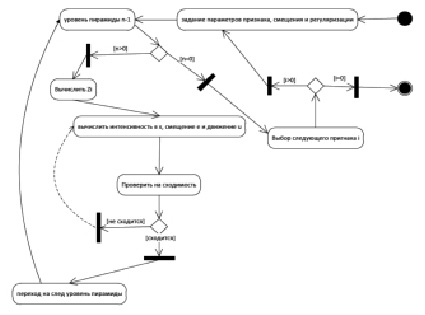
Диаграмма алгоритма Лукаса-Канаде
В заключение констатируем, что существуют различные варианты модификации метода Лукаса-Канаде, позволяющие улучшить его производительность и уменьшить количество ошибок, например, совмещение метода Лукаса-Канаде с методом Хорна-Шанка [5]. Дальнейшая работа в этом направлении имеет определенные перспективы.