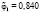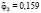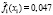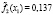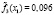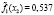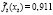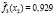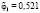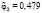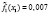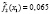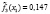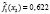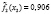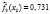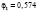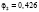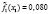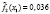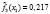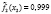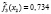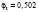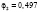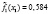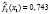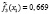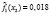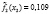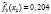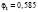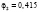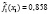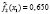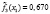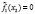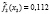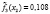Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

На сегодняшний день артериальная гипертензия является одной из наиболее значимых медико-социальных проблем Российской Федерации. Артериальная гипертензия – синдром повышенного артериального давления. Гипертоническая болезнь – это хронически протекающее заболевание, основным проявлением которого является артериальная гипертензия, не связанная с наличием патологических процессов. В табл. 1 представлена классификация уровней артериального давления (АД), включающей в себя значения систолического артериального давления (САД) и диастолического артериального давления (ДАД) при артериальной гипертензии и относительной нормы [1–2].

Таблица 1

Классификация уровней артериального давления

Кровь в организме человека оказывает на стенки кровеносных сосудов давление. Движение крови осуществляется под влиянием разности давлений между различными отделами сосудистого русла, создаваемого сердцем. Давление в артериях в момент, когда сердце сжимается и выталкивает кровь в артерии, определяет систолическое артериальное давление, оно зависит от силы сокращения сердца. Давление в артериях в момент расслабления сердечной мышцы определяет диастолическое артериальное давление. В качестве исходных показателей научного исследования используются альтернативные показатели, вторично характеризующие состояние артериальной гипертензии: приступы стенокардии, одышка, перебои в работе сердца (ПРС), головокружения и (или) обмороки (ГО), головные боли (ГБ), нарушения сна (НС), шум в ушах и (или) в голове (ШУГ). Данные показатели измерялись у лиц преклонного возраста с различной степенью артериальной гипертензии. Объем выборки составил 96 человек.

Построение алгоритма метода и его апробация на выше перечисленных показателях предполагает совместное использование латентной модели и ортогональной факторной структуры в формирование симптомокомплексов и построения диагностической шкалы [3–6]. Прежде чем излагать суть метода необходимо дать определения базовых терминов.

Определение. Диагностической шкалой в методе ФОРДИАСИМПТ называется набор апостериорных вероятностей полученных с помощью простейшей латентно-структурной модели и формулы Байеса, позволяющей отнести объект исследования к одному из двух сформированных классов.

Определение. Симптомокомплексом называется тройка альтернативных показателей, используемых для построения диагностической шкалы в методе ФОРДИАСИМПТ.

Определение. Два симптомокомплекса считаются зависимыми, если они содержат хотя бы один общий параметр, в противном случае эти симптомокомплексы независимы.

Первая задача ФОРДИАСИМПТ – сформировать набор симптомокомплексов опираясь на ортогональную факторную структуру с учетом уровня значимости Ţ φ коэффициента по χ2 критерию. Вторая задача ФОРДИАСИМПТ – для каждого симптомокомплекса найти диагностическую шкалу на базе простейшей латентно-структурной модели.

Первая задача решается посредством классического факторного исследования, но с учетом бинарности исходных показателей [3], [7]. Вторая – непосредственным переходом к построению латентной модели на базе альтернативных данных. Построение латентной модели подразумевает ввод следующих обозначений:

pi – отношение числа лиц, положительно ответивших на i-ый вопрос к общему числу респондентов;

pij – отношение числа лиц, положительно ответивших на i-ый и j-ый вопросы к общему числу респондентов;

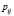– отношение числа лиц, положительно ответивших на i-ый и отрицательно на j-ый вопросы, к общему числу респондентов;

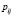– отношение числа лиц, отрицательно ответивших на i-ый и j-ый вопросы к общему числу респондентов;

pijk – отношение числа лиц, положительно ответивших на i-ый, j-ый и k-ый вопросы, к общему числу респондентов;

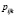– отношение числа лиц, положительно ответивших на i-ый и k-ый вопросы и отрицательно на j-ый, к общему числу респондентов;

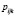– отношение числа лиц, отрицательно ответивших на i-ый и j-ый вопросы при положительном ответе на k-ый вопрос, к общему числу респондентов;

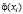– частота, соответствующая относительному объему i-го класса;

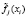– вероятность положительного ответа респондента на j-ый вопрос, находясь в i-ом классе;

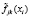– вероятность положительного ответа респондента на j-ый и k-ый вопросы, находясь в i-ом классе;

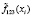– вероятность положительного ответа респондента на первый, второй и третий вопросы, находясь в i-ом классе.

Используя вышеуказанные обозначения при построении латентной модели на базе альтернативных показателей при наличии трех вопросов и двух латентных классов, получаем дискретные классы респондентов и разрешимую систему уравнений с дискретными переменными:

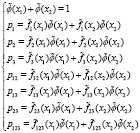(1)

Для упрощения в целях дальнейшего изложения введем функцию

,

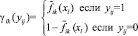где l – номер класса и может принимать значение 1 или 2, k – номер симптомокомплекса, 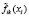– вероятность положительного ответа респондента из l-ого класса на i-ый вопрос, выбранный как параметр, составляющий симптомокомплекс, yij – значение ответа j-го респондента на i-ый вопрос. Условием вхождения параметров в зависимый или независимый симптомокомплекс является значение весовых нагрузок соответствующего фактора на уровне не ниже 0,5. Вероятность принадлежности первому классу вычисляется посредством формулы Байеса с использованием введенной функции

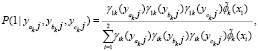(2)

где ak, bk, ck – номера трех параметров k-го симптомокомплекса.

Используя вторичные альтернативные признаки для формирования симптомокомплексов, можно определить при соответствующем знании степени гипертензии, какой тип лечения нужно применять к конкретному пациенту, выбрать тот или иной способ воздействия в зависимости от вероятностной принадлежности пациента к соответствующему симптомокомплексу. А в случае принадлежности индивидуума к нескольким симптомокомплексам с взаимоисключающим лечением подобрать щадящий режим лечения. Нахождение симптомокомплексов осуществлялось нижеследующем алгоритмом метода.

Алгоритм метода ФОРДИАСИМПТ:

1. Из матрицы исходных данных путем элементарного преобразования получаем матрицу стандартизованных данных.

2. Вычисляем корреляционную матрицу.

3. С целью исключения незначимых показателей вычисляем вероятностные значения уровней зависимости по формуле χ2 = n·φ, где n – объем выборки.

4. Определяем наименьшее количество выделяемых факторов (критерий Гуттмана, критерий «каменной осыпи» или другой адекватный критерий [3–4]).

5. Находим общности любым из известных методов [3], [7].

6. Вычисляем первичную ортогональную матрицу весовых нагрузок факторов A (метод главных факторов, метод минимальных остатков и т.д. [2–4]).

7. Полученную на предыдущем шаге матрицу весовых нагрузок подвергаем ортогональному вращению в соответствии с варимакс критерием [4], [8–9].

8. Осуществляем анализ ортогональной факторной структуры, полученной после вращения, и формируем зависимые и независимые симптомокомплексы.

9. Для каждого симптомокомплекса формируем диагностическую шкалу, вычисляя маргиналы и решая систему уравнений (1).

10. По формуле (2) вычисляем апостериорные вероятности для всех объектов исследования.

Таблица 2

Матрица коэффициентов корреляции пациентов с артериальной гипертензией

Таблица 3

Матрица значимости φ коэффициентов по χ2 распределению

Таблица 4

Матрица собственных значений корреляционной матрицы

Анализ табл. 4 позволяет сделать предварительную оценку по Гуттману того, что число общих факторов не меньше двух, т.к. имеются два собственных числа корреляционной матрицы больше (или равных) единице. Для оценки сверху количества выделяемых факторов использовался критерий, задаваемый формулой (3), величина которого асимптотически распределена по закону χ2 c числом степеней свободы, равным :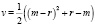

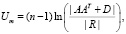(3)

где m – размерность выборки, r – количество выделяемых факторов, A – матрица весовых нагрузок факторов, R – корреляционная матрица, D – диагональная матрица факторного отображения характерных факторов. В нашем примере 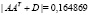, , 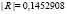v = 15, Um = 1,769678.

Очевидно, что Um не превышает даже высоко статистического уровня значимости, следовательно, выделение только двух факторов обоснованно.

Таблица 5

Матрица ортогонального факторного отображения после варимакс вращения, полученная методом минимальных остатков

Анализ матрицы весовых нагрузок позволил сформировать один независимый симптомокомплекс («Стенокардия, Одышка, ПРС») и четыре зависимых симптомокомплекса («ГО, ГБ, НС», «ГО, НС, ШУГ», «ГО, ГБ, ШУГ», «ГБ, НС, ШУГ»). Результаты представлены в нижеследующих таблицах.

Таблица 6

Основные показатели симптомокомплекса «Стенокардия, Одышка, ПРС» (№ 1)

Таблица 7

Основные показатели симптомокомплекса «ГО, ГБ, НС» (№ 2)

Таблица 8

Основные показатели симптомокомплекса «ГО, НС, ШУГ» (№ 3)

Таблица 9

Основные показатели симптомокомплекса «ГО, ГБ, ШУГ» (№ 4)

Таблица 10

Основные показатели симптомокомплекса «ГБ, НС, ШУГ» (№ 5)

Сформированные симптомокомплексы позволили выявить соответствующие подгруппы пациентов с артериальной гипертензий, к которым, в зависимости от вероятностной принадлежности к зависимым симптомокомплексам и независимому симптомокомплексу, проведено оптимальное или щадящие лечение. С точки зрения медицины набор зависимых симптомокомплексов отвечает за расстройства центральной системы, а независимый симптомокомплекс в большей степени характеризует нарушения в работе сердца.

Выводы

Реализован вычислительный алгоритм ФОРДИАСИМПТ, позволяющий строить диагностические симптомокомплексы на базе альтернативных данных, оптимальной ортогональной факторной структуры, простейшей латентно-структурной модели и формулы Байеса.

Полученный алгоритм ФОРДИАСИМПТ был апробирован на данных, характеризующих в качестве вторичных показателей состояние пациентов пожилого возраста при артериальной гипертензии. В результате работы алгоритма были выявлены четыре зависимых и один независимый симптомокомплексы, позволяющие подобрать индивидуальное лечение к каждому пациенту на базе вероятностной принадлежности к соответствующему набору симптомокомплексов и с учетом зависимости между ними.