Использование параллельных алгоритмов вычислений обеспечивает повышенный интерес разработчиков специализированных вычислительных устройств к модулярным кодам. Эти коды позволяют эффективно реализовать алгоритмы, которые содержат операции сложения, вычитания и умножение. Среди таких алгоритмов можно выделить алгоритмы цифровой обработки сигналов (ЦОС). Так как основными операциями алгоритмов цифровой обработки сигналов являются операции сложения, вычитания и умножения, то в ряде работ было предложено использовать алгебраические системы, обладающие свойством кольца и поля [1–5]. При этом особое внимание при использовании модулярных кодов уделяется вопросам обеспечения отказоустойчивости специализированных процессоров ЦОС.
Основная часть
Применение непозиционных модулярных кодов обеспечивает за счет параллельной работы с небольшими остатками обработку ЦОС с максимальным быстродействием. Такое состояние определяется тем, что математическую основу модулярных кодов составляют взаимно простые основания. В результате этого двоичный позиционный код числа модно представить в виде многомерного вектора вида
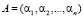, (1)
где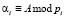 
– остаток, полученный при делении числа А на основание pi; i = 1,…,n; HOД(pi, pj), 
.
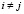Приведенное выражение (1) используется в системе остаточных классов (СОК). Для эффективной работы этого модулярного кода необходимо, чтобы значение числа А не превышало значения рабочего диапазона, которое задается равенством
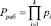, (2)
где k – количество информационных рабочих оснований СОК; k < n.
При этом СОК обеспечивает полный диапазон, который определяется из следующего равенства
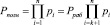, (3)
В работах [4–8], показано, что, если при переводе из модулярного кода в позиционный код, полученная величина числа (полинома) не превышает значение рабочего диапазона, то модулярный код не содержит ошибки.
В противном случае – модулярный код является запрещенным и содержит ошибку, как минимум в одном остатке.
Но основным недостатком любого модулярного кода является то, что он относится к непозиционным арифметическим структурам. То есть по данному коду невозможно определить его местоположения относительно рабочего диапазона. Поэтому при разработке алгоритмов поиска и коррекции ошибок в модулярных кодах используют позиционные характеристики [6–10]. В данной работе будет рассмотрен алгоритм обнаружения и исправления ошибок, который использует процедуру расширения системы оснований модулярного кода.
В данном алгоритме берется исходное число A = (a1,…,ak, ak + 1, ak + 2), которое имеет два контрольных основания, удовлетворяющих условию
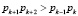, (4)
затем используя k информационных остатков a1, a2,…,ak, вычисляют остатки по контрольным основаниям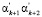 
. После этого необходимо определить величину синдрома ошибки по этим двум контрольным основаниям
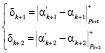(5)
В основу метода, базирующегося на вычислении синдрома ошибок по контрольным основаниям с использованием алгоритма расширения системы оснований, положено условие, согласно которому если синдром ошибки равен нулю, то это означает, что комбинация СОК не содержит ошибку.
Если кодовая комбинация СОК является запрещенной, то вычисленные значения остатков по контрольным основаниям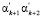 
не совпадет с исходными величинами остатков избыточных оснований ak + 1 и ak + 2. При этом по величине синдрома ошибки можно однозначно определить ошибочное основание, а также величину ошибки.
Рассмотрим пример использования алгоритма расширения оснований. В данном алгоритме синдром ошибки будет определяться выражением
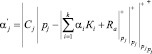, (6)
где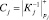 
; Ra – ранг числа A в безизбыточной СОК; 
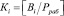; j = k + 1, k + 2.
Как отмечалось ранее, если в системе остаточных классов с рабочими p1, p2,…, pk и контрольными основаниями pk+1, pk+2, удовлетворяющих условию (4), модулярная кодовая конструкция A = (a1, a2,…, ak + 2) не содержит ошибок, если выполняется условие
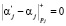, (7)
Пусть задана система остаточных классов с рабочими основаниями р1 = 2, р2 = 3, р3 = 5. Тогда рабочий диапазон данной системы СОК будет равен Pраб = 30. В качестве контрольных оснований выберем основания р4 = 7 и р5 = 11. В этом случае полный диапазон такой системы Pполн = 2310.
Вычислим ортогональные базисы полной СОК. В данной полной системе основания ортогональные базисы равны
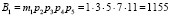
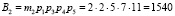
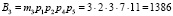
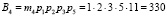
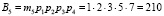
Представим ортогональные базисы, чтобы реализовать алгоритм (6)
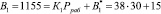
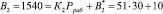
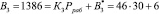
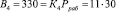
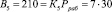
Проведем расчет по модулю р4 = 7
; 
; 
; 
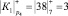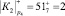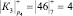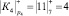
Определим величину
.
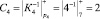Проведем расчет по модулю р5 = 11
; 
; 
; 
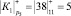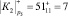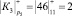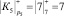
Определим величину
.
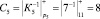Пусть имеем число А = (0, 2, 2, 2, 2) = 2. Вычислим значение остатков по контрольным основаниям для данного числа, используя разработанный алгоритм.
Вычислим значение ранг в безизбыточной системы, определяемые основаниями р1=2, р2 = 3, р3 = 5.
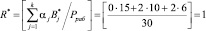
Тогда вычисленное значение первого остатка по контрольному основанию р4 = 7 для данной комбинации
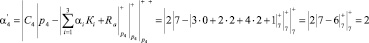
Вычисленное значение первого остатка по контрольному основанию р5 = 11 для данной комбинации
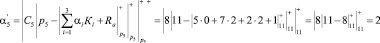
Теперь определим величину синдрома ошибки согласно (7)
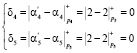
В результате синдром ошибки равен нулю, то это соответствует тому, что комбинация СОК А = (0, 2, 2, 2, 2) не содержит ошибки.
Пусть ошибка произошла по первому основанию и ее глубина равна ∆a1 = 1. Тогда модулярный код имеет вид А* = (1, 2, 2, 2, 2) = 2. Вычислим значение синдрома ошибки для данного числа, используя разработанный алгоритм.
Вычислим значение ранг в безизбыточной системы, определяемые основаниями р1 = 2, р2 = 3, р3 = 5.
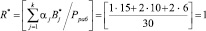
Тогда вычисленное значение первого остатка по контрольному основанию р4 = 7 для данной комбинации
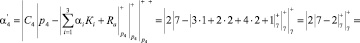
Вычисленное значение первого остатка по контрольному основанию р5 = 11 для данной комбинации
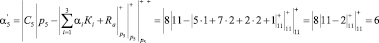
Теперь определим величину синдрома ошибки согласно (7)
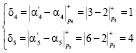
В результате синдром ошибки отличен от нуля, то это соответствует тому, что комбинация СОК А* = (1, 2, 2, 2, 2) содержит ошибку.
Так как ошибочное число определяется из условия
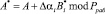, (8)
то для получения нулевого синдрома ошибки необходимо из полученного синдрома вычесть значения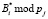 
, где i = 1, 2, …, k; j = k + 1, k + 2.
Так значение безизбытоного ортогонального базиса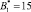 
, то значения коррекции будут равны
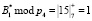
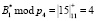
Вычисленные значения совпадают с полученным синдромом ошибки. Это соответствует тому, что ошибка произошла по первому основанию, а ее глубина равна единице.
В таблице приведены значения ошибок по основаниям модулярного кода и соответствующие им номера интервалов.
Распределение однократных ошибок кода СОК
|
Основание СОК |
Глубина ∆αi |
δ4 |
δ5 |
|
p1 = 2 |
1 |
1 |
4 |
|
p2 = 3 |
1 |
3 |
10 |
|
2 |
6 |
9 |
|
|
p3 = 5 |
1 |
6 |
6 |
|
2 |
5 |
1 |
|
|
3 |
4 |
7 |
|
|
4 |
3 |
2 |
|
|
p4 = 7 |
1 |
1 |
0 |
|
2 |
2 |
0 |
|
|
3 |
3 |
0 |
|
|
4 |
4 |
0 |
|
|
5 |
5 |
0 |
|
|
6 |
6 |
0 |
|
|
p5 = 11 |
1 |
0 |
1 |
|
2 |
0 |
2 |
|
|
3 |
0 |
3 |
|
|
4 |
0 |
4 |
|
|
5 |
0 |
5 |
|
|
6 |
0 |
6 |
|
|
7 |
0 |
7 |
|
|
8 |
0 |
8 |
|
|
9 |
0 |
9 |
|
|
10 |
0 |
10 |
Для реализации алгоритма (6) была разработана структура вычислительного устройства, осуществляющего процедуру поиска и исправления ошибок на основе расширения системы оснований. Структура данного устройства показана на рисунке.
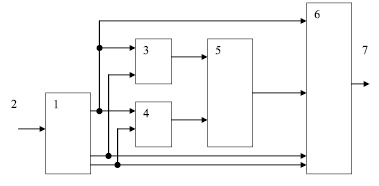
Структура устройства обнаружения и коррекции ошибки на основе расширения системы оснований
Устройство функционирует следующим образом. На вход 2 устройства для обнаружения и исправления ошибок в СОК подается контролируемое число, представленное в полиномиальной форме
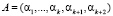. (9)
Данный вектор записывается в регистр 1. На вход первого 3 блока вычисления синдрома с выходов регистра 1 подается
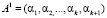(10)
c образованием на его выходе сигнала
δ1=(α k+1-α* k+1))mod рk+1. (11)
При этом
α* k+1=λ(1)1α1+ λ (1)2α2+…+ λ(1)kαk , (12)
где λ(1)i – константы системы СОК.
На входы блока 4 вычисления синдрома с выходов регистра 2 подается
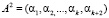. (13)
С образованием на выходе сигнала
δ2=(α k+2+ α *k+2)mod pk+2. (14)
При этом
α*k+2= λ(2)1α1+ λ(2)2α2+…+ λ(2)kαk , (15)
где λ(2)i – константы системы.
Величины δ1 и δ2 в двоичном виде поступают на входы блока 5 памяти и выбирают оттуда соответствующую константу ошибки. Эта константа ошибки поступает в сумматор 6, где суммируется с искаженным A*, представленном в непозиционном виде поданным из регистра 1. Исправленное представление A с выхода сумматора 6 подается на выход 7 устройства.
Выводы
Современные модулярные коды позволяют повысить скорость выполнения алгоритмов ЦОС за счет параллельной обработки малоразрядных остатков. Кроме того эти коды также позволяют осуществлять поиск и коррекцию ошибок, которые могут возникать в процессе функционирования непозиционного спецпроцессора. В работе приведен пример реализации алгоритма поиска и коррекции ошибки, который использует расширение системы оснований. В статье приведена структура устройства коррекции модулярного кода, использующего разработанный алгоритм.