Во многих сферах деятельности человека все чаще стали применять информационные технологии. Наиболее широкое применение они нашли в области инфотелекоммуникационных систем. Особое внимание в таких системах уделяется цифровой обработке сигналов (ЦОС). Для обеспечения реального масштаба времени обработки сигналов применяются параллельные алгоритмы вычислений. Однако это приводит к значительному усложнению вычислительных систем. Чтобы обеспечить надежную работу таких вычислительных устройств в работе предлагается использовать модулярные коды, которые позволяют обнаруживать и исправлять ошибки, возникающие в процессе функционирования.
Постановка и решение задачи исследования. Использование параллельных алгоритмов вычислений в современных информационных технологиях обусловлено высокими требованиями, предъявляемыми к скорости обработки информации. Чтобы обеспечить данное требование в ряде работ предлагается использовать модулярные коды [1–6]. Модулярные коды относятся к арифметическим кодам, которые применяются для выполнения алгоритмов, в которых используются модулярные операции – сложение, вычитание и умножение по модулю.
Так в системе остаточных классов (СОК) числа, которые принадлежат рабочему диапазону можно однозначно представить в виде набора остатков
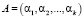, (1)
где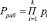 
. – рабочий диапазон; А < Pраб; 
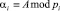; i = 1,2,…,k.
Тогда для суммы, разности и произведения двух чисел А и В, имеющих соответственно модулярные коды (a1,a2,…,ak) и (b1, b2,…, bk) справедливы соотношения при i = 1,…,k
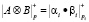, (2)
где ● – операции сложения, вычитания и умножения по модулю.
Тогда ортогональное преобразование сигнала определяется
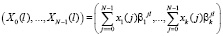, (3)
где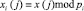 
– остаток по модулю отсчета входной последовательности 
; 
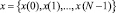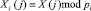– остаток по модулю спектрального отсчета сигнала 
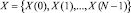; β – поворачивающий коэффициент дискретного преобразования Фурье.
При этом обратное ортогональное преобразование сигнала определяется
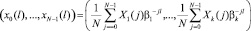, (4)
Так как эти модулярные коды работают с остатками, то благодаря малоразрядности обрабатываемых остатков, реализация алгоритмов ЦОС проводится в реальном масштабе времени. При этом такие вычисления осуществляются параллельно по независимым вычислительным каналам, которые определяются модулями кода.
При этом независимость обработки остатков может быть положена в основу построения избыточных модулярных кодов. Так как в процессе вычислений ошибочный результат не выходит за пределы, то очевидно, что ошибка не распространяется на другие вычислительные тракты. Следовательно, чтобы исправить ошибку, которая возникла из-за отказа вычислительного оборудования одного из трактов необходимо выявить отказавший модуль и определить глубину ошибки.
Для построения избыточных модулярных кодов необходимо в данный набор оснований ввести дополнительные модули. В работе [7] показано, что для обнаружения и коррекции однократной ошибки необходимо ввести два контрольных основания, которые будут удовлетворять требованию
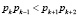. (5)
В этом случае происходит расширение диапазона системы остаточных классов.
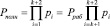. (6)
При этом такой диапазон разбивается на две части. Первую составляет рабочий диапазон, который содержит все разрешенные комбинации СОК. Если комбинация модулярного кода рабочему принадлежит диапазону СОК, т.е.
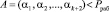, (7)
то она считается разрешенной.
При этом при возникновении ошибки такая комбинация переносится в область запрещенных комбинаций. Это связано с тем, что однократная ошибка переводит разрешенную комбинацию А = (a1,a2,…,ak+2) в комбинацию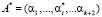 
, где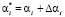 
– искаженный остаток, ∆ai – глубина ошибки. В результате воздействия ошибки искаженное число выходит за пределы рабочего диапазона и переносится в диапазон полный. Значит если определить местоположение искаженной комбинации 
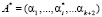, то можно однозначно выявить модуль, по которому произошла ошибка, а также определить ее величину ∆ai.
Чтобы провести эту процедуру в непозиционных модулярных кодах применяют различные позиционные характеристики [7–10]. Среди множества позиционных характеристик особое место занимает интервальный номер. Эта позиционная характеристика имеет достаточно простой физический смысл, так как задается следующим выражением
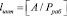. (8)
Как показывает анализ равенства (8), для вычисления позиционной характеристики необходимо выполнить операцию деления, которая не является модульной операцией. Следовательно, чтобы реализовать данную немодульную операцию необходимо выполнить совокупность модульных операций в непозиционном коде. Так в работе [5] показан алгоритм, с помощью которого можно осуществить обнаружение и исправление ошибки в коде классов вычетов, используя данную позиционную характеристику.
Однако данный алгоритм характеризуется значительными схемными затратами, так как все вычисления производятся по составному модулю. Отказ от работы с составным основанием позволяет уменьшить схемные затраты.
Проведем усовершенствования этого алгоритма. Рассматривая алгоритмы вычисления интервального номера числа, представленного в модулярном коде СОК, нельзя не отметить связь данной позиционной характеристики с характеристикой след числа. Применение позиционной характеристики следа позволяет однозначно определять номер интервала, в которой попадает ошибочное число A* при возникновении ошибки.
Если в упорядоченной системе СОК, содержащей k информационных и два избыточных оснований, в результате нулевизации модулярного кода числа A получен позиционная характеристика след
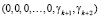, (9)
то интервал, в который будет перенесена ошибочная комбинация СОК числа A*, будет вычисляться
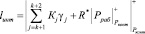, (10)
где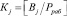 
; Bj – ортогональный базис по j-му основанию СОК;
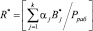– ранг в безизбыточной системы; 
.
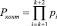Чтобы доказать правильность усовершенствованного алгоритма вычисления интервального номера числа покажем, в начале, что если хотя бы один след числа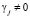 
, где j =k+1, k+2, то код СОК числа A является запрещенным. Другими словами, код СОК содержит ошибку. Для этого проведем замену произведения двух контрольных оснований СОК одним составным основанием 
.
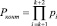Тогда исходный код СОК числа A, который задается в виде (k + 2) – мерного вектора, (a1,a2,…,ak+1, ak+2), примет вид
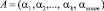, (11)
где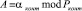 
.
Известно, что если в коде СОК числа A, принадлежащего рабочему диапазону СОК, произошла ошибка, то результатом операции параллельной нулевизации кода числа A* с использованием псевдоортогональных базисов Aik будет отличный от нуля след числа
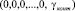, (12)
где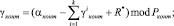 
;
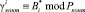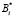– ортогональный базис безизбыточной системы оснований СОК.
С другой стороны, согласно китайской теореме об остатках (КТО)
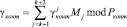, (13)
где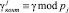 
; Мj – ортогональный базис системы модулярного кода с контрольными основаниями pk+1 и pk+r.
Очевидно, что если след отличен от нуля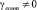 
, то хотя бы один из остатков 
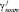должен отличаться от нуля.
Таким образом, если в результате параллельной нулевизации кода СОК числа A* и с помощью псевдоортогональных базисов будет получен след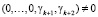 
, то данный полином содержит ошибку.
Покажем теперь, что величина интервального номера l кода СОК числа A будет определяться согласно алгоритма (10).
Пусть в результате процедуры нулевизации кода СОК искаженного числа A* получим след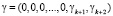 
отличный от нуля. Известно
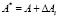, (14)
где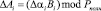 
; ∆ai – глубина ошибки по i-ому основанию.
При этом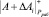 
= γ = (0,0,0,...,0,γk + 1, γk + 2).
Тогда на основании выражения (14) имеем
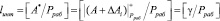. (15)
Согласно КТО и с учетом ai = 0, i = 1,2,…,k, имеем
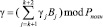. (16)
Подставляем (16) в равенство (15) получаем
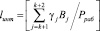. (17)
Учитывая подобие ортогональных базисов и делимость без остатка ортогональных базисов контрольных оснований на рабочий диапазон, а также количество переходов за пределы рабочего диапазона, имеем
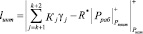, (18)
где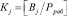 
.
В результате проведенных математических выкладок была показана связь позиционной характеристики интервальный номер с характеристикой след числа. Проведенные исследования показали, что использование данного усовершенствованного алгоритма вычисления интервального номера позволяет обеспечить коррекцию всех однократных ошибок и до 90 процентов двукратных ошибок.
Выводы
Для эффективной работы систем цифровой обработки сигналов, функционирующих в СОК, необходимо, чтобы время необходимое на выполнение операции вычисления позиционной характеристики не превышало времени выполнения процедуры преобразования из модулярного кода в позиционный код. Проведенные исследования показали, что переход к усовершенствованному алгоритму позволяет сократить время вычисления позиционной характеристики при обработке 24-разрядных данных на 14,1 % по сравнению с классическим методом вычисления интервального номера числа.