Одной из наиболее частых операций по управлению автотранспортным средством (АТС) является плавное (служебное) торможение, которое применяется водителем в штатных дорожно-транспортных ситуациях для снижения скорости движения и останова АТС в заранее выбранном положении [3]. Неправильный выбор усилия торможения или нестабильность навыка плавного торможения вызывают ощущение дискомфорта у пассажиров, а также могут вызвать дорожно-транспортное происшествие, связанное как с экономическими потерями, так и с ущербом здоровью человека.
Для исследования процесса полного плавного торможения АТС перед неподвижным объектом, находящимся на пути следования АТС, проведено имитационное моделирование движения АТС. Имитационная модель разработана на основе предложенной ранее математической модели, опубликованной в работе [2], моделирование проводилось с применением разработанного программного обеспечения.
Структурная схема имитационной модели приведена на рис. 1, под блоками которой приведены множества констант, причем константы блока «Генератор управляющих действий» соответствуют параметрам торможения, а константы блока «Математическая модель» соответствуют условиям моделируемой дорожной ситуации. Выход P блока математической модели принимает значение «ЛОЖЬ» в процессе вычислительного эксперимента и значение «ИСТИНА», когда он окончен; выход D принимает значение «ИСТИНА», если было допущено столкновение, и значение «ЛОЖЬ» в обратном случае; выход L соответствует текущему значению расстояния от АТС до неподвижного объекта.
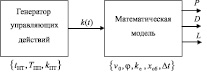
Рис. 1. Структурная схема имитационной модели. Обозначения величин в тексте
Зададим зависимость углового положения педали тормоза, прямо пропорционального усилию торможения и замедлению АТС, от времени t как функцию нормированного коэффициента k(t), принимающую значения от 0 (педаль отпущена) до 1 (педаль нажата полностью). Анализ рассматриваемого процесса показывает, что функция k(t), соответствующая выполнению водителем АТС полного плавного торможения без корректировки усилия торможения, имеет вид, приведенный на рис. 2, где kпт – уровень углового коэффициента k, соответствующий выбранному водителем замедлению АТС в ходе плавного торможения; TПП – время переходного процесса, во время которого коэффициент k изменяется от 0 до значения kпт, tНТ – момент времени начала торможения; tост – момент времени останова АТС.
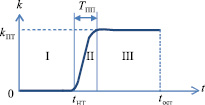
Рис. 2. Вид функции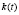 
, характерной для плавного торможения без корректировки усилия торможения. Обозначения в тексте
Блок «Генератор управляющих действий» через равные промежутки времени ∆t, подает на вход математической модели дискретные значения коэффициента k, формирующие совокупность значений функции k(t), которые вычисляются в зависимости от текущего значения модельного времени t и соответствующего ему участка I-III (рис. 2), по формуле:
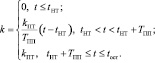
Отметим, что на участке II функция k(t) аппроксимируется линейно.
Зададим условия моделируемой дорожной ситуации, в соответствие с которыми начальная скорость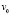 
принимается равной максимальной разрешенной в населенном пункте – 60 км/ч; тип дорожного покрытия – сухому асфальтобетонному; категория АТС – легковому автомобилю 
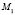; коэффициент φ сцепления колеса с опорной поверхностью – 0,8 [5]; коэффициент 
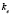эффективности торможения – 1,28 [5]; положение 
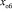неподвижного объекта – 145 м; интервал времени 
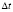, на величину которого происходит дискретное изменение времени t модели – 10 мс [1].
Ввиду детерминированности рассматриваемой имитационной модели, моделирование выполним путем перебора значений параметров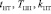 
функции 
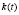. Обозначим интервалы и соответствующие им шаги изменения параметров в ходе моделирования:
,
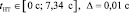где левая граница интервала соответствует моменту начала отсчета, а правая – значению величины максимального момента времени, начало торможения в который и после которого приводит к столкновению, независимо от дальнейших управляющих действий водителя АТС.
,
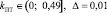где правая граница принята равной значению коэффициента k, соответствующему замедлению АТС, равному 3 м/с2 [4].
,
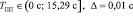где правая граница соответствует максимальному значению времени нажатия педали тормоза, вычисленному в начальный момент времени при изменении коэффициента k от нуля до максимального рассматриваемого значения величины kпт, равного 0,49.
Перебор каждого параметра внутри соответствующего интервала начинается с левой границы, если она входит в интервал, и с первого значения, большего левой границы на величину шага D, в обратном случае. Значение параметра последовательно увеличивается на шаг D до достижения правой границы рассматриваемого интервала включительно. С каждым набором параметров проводится вычислительный эксперимент, целью которого ставится определение наличия или отсутствия столкновения (величина D) АТС с неподвижным объектом и вычисление расстояния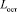 
между остановившимся АТС и неподвижным объектом в результате торможения.
Результаты вычислительных экспериментов, в которых расстояние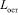 
сравнительно велико (условно выбран порог, равный 30 м), исключаются из рассмотрения, поскольку они отражают процессы торможения, приводящие к преждевременному останову АТС, что не соответствует рассматриваемой дорожной ситуации.
Получены следующие результаты имитационного моделирования движения АТС в процессе полного плавного торможения:
- всего вычислительных экспериментов - 55066935;
- из них экспериментов без столкновений АТС с неподвижным объектом - 7119668;
- из них экспериментов без столкновений АТС с неподвижным объектом, в которых
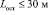- 4401532; - максимальное значение момента времени
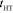начала торможения, при котором водитель имеет возможность выполнить плавное торможение, с - 5,91; - минимальное значение коэффициента
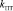углового положения педали тормоза, при котором водитель имеет возможность избежать столкновения - 0,16.
Рассмотрим частный случай, когда момент времени начала торможения совпадает с началом отсчета (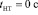
). На рис. 3 представлена область значений параметров торможения kпт и TПП при 
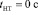, на которой различными цветами показаны диапазоны соответствующих значений расстояния 
.
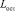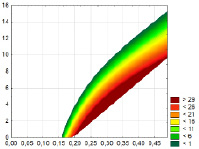
Рис. 3. Область значений параметров торможения kпт и TПП при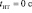 
. По горизонтальной оси – значения параметра kпт, безразмерные единицы; по вертикальной оси – значения параметра TПП, с. Различными цветами показаны диапазоны соответствующих значений расстояния 
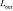(пояснение справа)
Аппроксимация данных имитационного моделирования выполнялась по методу наименьших квадратов полиномиальными функциями степени не выше 2.
Получена система неравенств, описывающая в 96,1 % случаев область значений параметров плавного торможения kпт и TПП при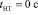 
, представленной на рис. 3, записанная следующим образом:
На рис. 4 приведена область значений параметров торможения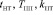 
. Для наглядности представленной диаграммы шаги изменения параметров были увеличены до значений 0,1 с, 0,1 с и 0,05 соответственно.
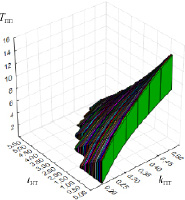
Рис. 4. Область значений параметров торможения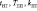 
. На обозначенных осях приведены значения параметров tнт и TПП в секундах, параметра kпт – в безразмерных единицах. Различными цветами показаны разрезы области значений по плоскостям, параллельным плоскости, проходящей через оси параметров kпт и TПП, при различных значениях параметра tнт
Получена система неравенств, описывающая в 97,3 % случаев область значений параметров плавного торможения tнт, kпт и TПП, представленной на рис. 4, записанная следующим образом:
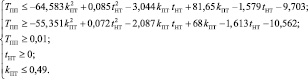
Таким образом, в результате имитационного моделирования движения АТС построена область значений параметров полного плавного торможения, не приводящих к столкновению АТС с неподвижным объектом с ограничением на расстояние между ними. Получена информация о соответствии параметров результату плавного торможения (расстоянию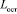 
), которая может быть использована для оценки плавности выполняемого водителем АТС торможения путем сравнения значений индивидуальной функции 
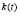с аналогичной, на основе которой был выполнен вычислительный эксперимент.