Оптимизация технического решения пьезоэлектрического сканера состоит в минимизации функции f(x) = f(x1, x2, …, xn), где x определяется явными ограничениями
lj ≤ xj ≤ uj при j=1, 2, …, n, (1)
а также неявными ограничениями
gi(x)≤bi при i=1, 2, …, m. (2)
Если целевая функция f(x) выпукла и функции gi(x) тоже выпуклы, то задача будет иметь единственное решение. Значения lj и uj являются нижней и верхней границами переменных. Если в конкретной задаче заданные переменные теоретически не имеют ограничений, то предположение о наличии у них «безопасных» границ, т. е. границ, включающих оптимум, позволит применить комплексный метод.
Данный метод является итерационным. В нем предполагается, что известны значения n и m, lj и uj и начальная точка (см. неравенства(1) и (2)). В первую очередь необходимо выбрать k точек, которые удовлетворяют ограничениям, а также вычислить целевую функцию во всех k точках. Множество этих точек называется комплексом. Бокс обнаружил, что должно быть больше (n+1) – числа точек, используемых в симплексном методе Нелдера-Мида, и положил k=2n.
Как упоминалось выше, предполагается, что точка x1, удовлетворяющая всем ограничениям для пьезоэлектрического сканера, задана. Остальные точки, удовлетворяющие неравенству (1), могут быть выбраны следующим образом:
xij=lj+r(uj-lj) (3)
для j=1, 2, …, n и i=2, 3, …, k, где r – псевдослучайная равномерно распределенная переменная в интервале (0; 1).
Точки, выбираемые в соответствии с уравнением (3) для данного j, будут автоматически удовлетворять неравенству (1). Если эти точки удовлетворяют также неравенству (2), то они принимаются в качестве начальных точек комплекса. Если точка, выбранная в соответствии с уравнением (3), не удовлетворяет неравенству (2), то она смещается на половину расстояния до центра тяжести множества уже принятых точек, т. е. формируется точка
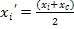 , (4)
, (4)
где 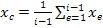 (5)
(5)
Если точка в соотношении (4) все еще не является допустимой, то описанная соотношением (3) процедура повторяется вновь до тех пор, пока точка не станет допустимой. Если функция gi(x) выпукла, то в конце концов ограничения будут выполняться. Конечно, поскольку точка x1 находится внутри области ограничений пьезосканера, то комплекс будет состоять из допустимых точек.
Удобно упорядочить точки комплекса в соответствии со значениями функции. Процедуру инициализации комплекса можно описать с помощью блок-схемы (рис.1). Она реализуется в программе операторами в строках с номерами до 1000.
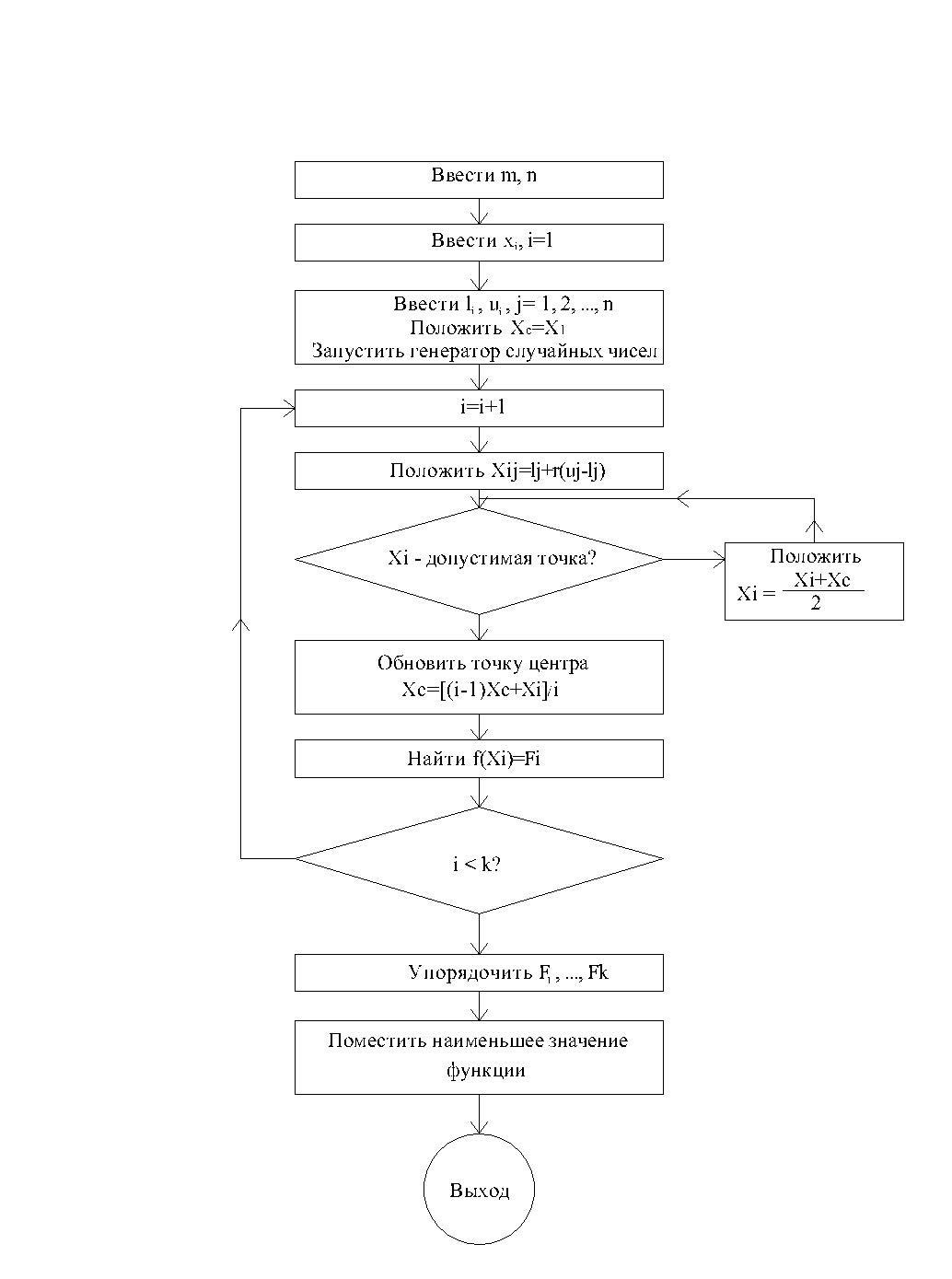
Рис. 1.
Теперь мы подошли к итерационной процедуре комплексного метода, в которой производится поиск минимума перемещением по направлению к минимуму внутри области ограничений. Для этой процедуры необходимы следующие шаги:
1. Найти точку с наибольшим значением функции xh и найти центр x0 остальных (k-1) точек пьезосканера.
2. Попытаемся сместиться от точки xh и получить при этом точку xr отражением точки xh относительно точки x0, используя коэффициент отражения α>1, что можно записать как
xr=(1+ α)x0-αxh. (6)
3. Проверить, является ли точка xr допустимой.
а) Если точка xr не является допустимой и не выполняется ограничение для lj, то полагаем xrj=lj+10-6; если не выполняется ограничение для uj, то полагаем xrj=uj-10-6
б) Если не выполняются ограничения, то точку xr перемещают на половину расстояния между xr и центром x0, т. е.
xr (новое) = (xr+x0 )/2. (7)
Затем производится повторная проверка на допустимость и шаг 3 повторяется до тех пор, пока не будет получена допустимая точка.
4. Если точка xr является допустимой, то вычисляется значение функции f(xr) и сравнивается с f(xk ) – наибольшим значением функции пьезосканера.
Если f(xr )>(xk ), т. е. «хуже», чем наибольшее значение, полученное ранее, то точка xr смещается к центру x0 на половину расстояния между ними, т. е.
xr (новое) = (xr+x0)/2
и процесс возвращается на шаг 3.
5. Если f(xr )<f(xk ), то точка x заменяется на точку xr, затем точки и значения функции комплекса снова упорядочиваются.
6. Вычисляются две величины, использующиеся при проверке сходимости метода: среднее квадратическое отклонение σ для k значений функции и максимальное расстояние dm между двумя точками пьезосканера. Первая величина вычисляется как
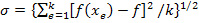 , (8),
, (8),
где 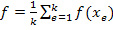 , (9)
, (9)
но для вычисления σ2 лучше использовать формулу
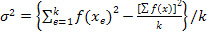 . (10)
. (10)
7. Величины σ2 и dm проверяются на сходимость. Если обе эти величины достаточно малы, то процедура поиска минимума заканчивается. В противном случае необходимо вернуться на шаг 1 и повторить процедуру для другой конструкции пьезосканера.
8. Оптимизация технического решения пьезосканера состоит, в частности, в разработке оптимальной конструкции биморфных элементов пьезосканера.
При разработке биморфных элементов пьезосканера в нанотехнологии необходим учет их поперечных и продольных колебаний, оказывающих существенное влияние на точность позиционирования острия кантилевера относительно подложки для наиболее точного нанесения квантовых точек на подложку. Различные конструкции кантилевера привносят в устройство свои особенности.
Пьезосканер должен работать в режиме антирезонанса, то есть все резонансные частоты должны быть исключены. Это достигается как геометрией пьезосканера, так и материалом.
Примером устройства, в котором более существенную роль играют поперечные колебания биморфного элемента, может послужить устройство возбуждения кантилевера, представленного на рис. 2.
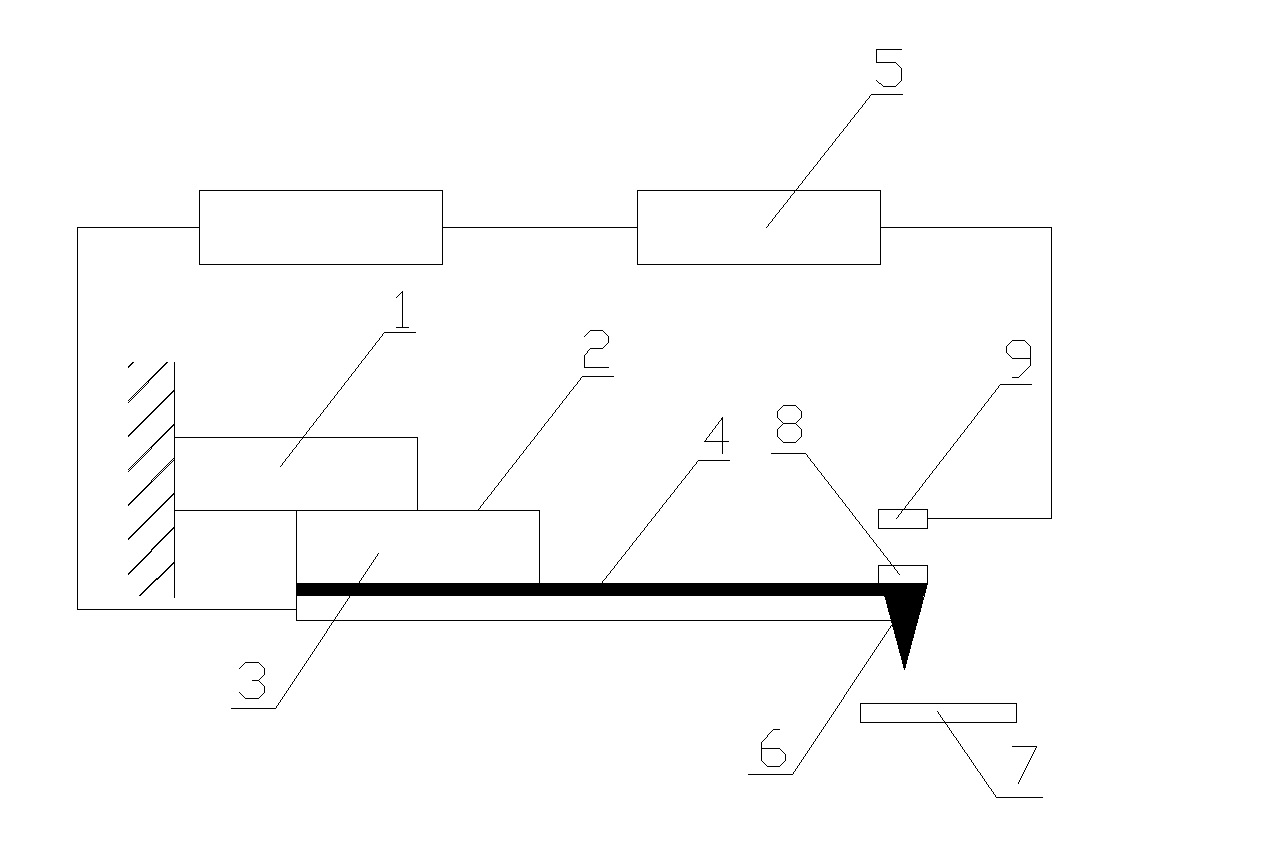
Рис. 2. Устройство возбуждения кантилевера
Устройство возбуждения кантилевера содержит держатель кантилевера 1 с кантилевером 2, включающим основание 3 с гибкой балкой 4, источник возбуждения колебаний 5 гибкой балки 4 с остриев 6 относительно образца 7; на гибкой балке 4 в зоне расположения острия 6 закреплена круглая магнитная нанопластинка 8, а источник возбуждения колебаний 5 гибкой балки 4 с острием 6 выполнен в виде генератора магнитных колебаний 9 с рабочими частотами до 200 кГц.
Устройство возбуждения кантилевера работает следующим образом: при изменении частоты генератора магнитных колебаний 9 изменяется и частота колебаний гибкой балки 4 с острием 6 в результате взаимодействия круглой магнитной нанопластинки 8 с генератором магнитных колебаний 9, который выполнен на базе стандартной катушки индуктивности с сердечником (условно не обозначена).
Перейдем к собственным формам колебаний биморфного элемента и функциям, их определяющим.
Собственные формы колебаний биморфного элемента и функции, их определяющие.
Простейшим периодическим решением уравнения свободных колебаний биморфного элемента
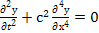 (11)
(11)
является так называемое главное колебание, в котором y(x,t) изменяется с течением времени по гармоническому закону
y(x,t)=φ(x)sin(ωt+α) (12).
φ(x) – функция, устанавливающая закон распределения максимальных (амплитудных) отклонений точек оси биморфного элемента от равновесного расположения, называется формой главного колебания или собственной формой.
ω – собственная частота.
Отбор собственных частот и соответствующих им собственных форм осуществляется с помощью уравнения собственных форм и краевых условий задачи.
Уравнение собственных форм однородной задачи:
EJφIV(x) – ω2μφ(x)=0 (13)
или φIV(x) – k4φ(x)=0 (14),
где k4=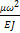 (15)
(15)
или k4=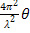 (16)
(16)
Уравнение (4) имеет следующие четыре независимых частных решения:
coskx, sinkx, chkx, shkx, его общий интеграл:
φ(x)=Acoskx+Bsinkx+Cchkx+Dshkx (17)
Он содержит четыре произвольные постоянные A, B, C, D, которые должны быть подобраны так, чтобы для функции φ(x) выполнялись краевые условия, т. е. условия закрепления концов биморфного элемента. В обычных случаях число краевых условий равно числу произвольных постоянных – по два на каждом конце. Все они выражаются равенствами нулю двух из следующих четырех величин: φ(x), φ’(x) ,φ’’(x), φ’’’(x),
пропорциональных соответственно прогибу, углу поворота, изгибающему моменту и перерезывающей силе в точках x=0 или x≡ℓ. Выполняя эти условия, мы получим четыре однородных уравнения, из которых найдутся отношения постоянных A, B, C, D и уравнение для определения собственных частот системы.
Во многих отношениях более удобной оказывается следующая система частных решений уравнения (14):
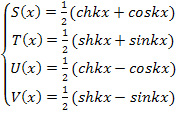 (18)
(18)
Функции S, T, U, V называются функциями А.Н. Крылова.
Найдем значения этих функций и их производных по аргументу kx до третьего порядка включительно при x=0 (формула 19):
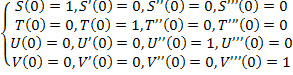
Определитель, составленный из этих величин, равен единице. Поэтому функции Крылова называют иногда функциями с единичной матрицей, а систему (18) – нормальной или фундаментальной системой интегралов уравнений (14).
Запишем уравнение (17) и представим тригонометрические функции в системе уравнений (18) через функции Крылова:
φ(x)=AS(x)+BT(x)+CU(x)+DV(x) (20)
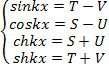 (21)
(21)
Приведем выражения последовательных производных по x от функций S(x), T(x), U(x), V(x) до четвертого порядка включительно.
|
Первая производная |
Вторая производная |
Третья производная |
Четвертая производная |
|
|
S(x) |
kV(x) |
k2U(x) |
k3T(x) |
k4S(x) |
|
T(x) |
kS(x) |
k2V(x) |
k3U(x) |
k4T(x) |
|
U(x) |
kT(x) |
k2S(x) |
k3V(x) |
k4U(x) |
|
V(x) |
kU(x) |
k2T(x) |
k3S(x) |
k4V(x) |
Одним из преимуществ функций Крылова является то, что с помощью этих функций можно сразу написать выражение общего интеграла уравнения (14), удовлетворяющего условиям на конце x=0 и содержащего только две постоянные, которые определяются из условий на другом конце x=ℓ.
Основная задача функций Крылова. Колебания биморфного элемента, жестко закрепленного концом x=0 и свободного на конце x=ℓ. Краевые условия в этом случае:
φ(0)=φ’(0)=0,
φ’’(ℓ)=φ’’’(ℓ)=0.
Интеграл уравнения (14), удовлетворяющий условиям на конце x=0, имеет вид:
φ(x)=CU(kx)+DV(kx) (22)
Условия на конце x=ℓ выражаются уравнениями:
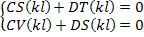 (23),
(23),
откуда
S2-TV=0 или ch(kℓ)cos(kℓ)+1=0 (24).
По таблицам находим первые четыре корня уравнения (24):
kℓ = 1.875; 4.694; 7.855; 10.996.
Для первых четырех собственных частот получаем по формуле (15)
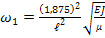 (25),
(25),
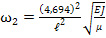 (26),
(26),
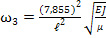 (27),
(27),
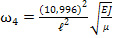 (28),
(28),
Расчет периода колебаний: 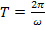 (29)
(29)
с учетом формулы (29) приведет к расчету первых четырех периодов колебания биморфного элемента:
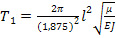 (30),
(30),
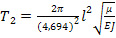 (31),
(31),
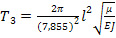 (32),
(32),
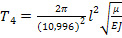 (33).
(33).
При иных заданных начальных параметрах можем перейти к другой форме записи собственных частот и периодов.
Запишем выражение для нахождения погонной массы для биморфного элемента: 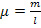 (34).
(34).
Учитывая формулы для вычисления массы m=ρV и объема V=bhℓ, получим выражение для погонной массы: μ=ρbh (35).
Момент инерции прямоугольного сечения определяется из известного выражения: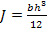 (36).
(36).
Стандартное выражение для вычисления первых четырех собственных частот выглядит согласно формулам (25-28).
Подставляя в (25-28) вместо величин E, μ и J (35) и (36), имеем следующие выражения для определения первых четырех частот биморфного элемента:
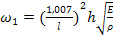 (37),
(37),
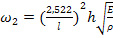 (38),
(38),
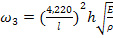 (39),
(39),
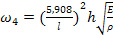 (40).
(40).
Учитывая выражение (19), получим окончательный вид первых четырех периодов колебаний биморфного элемента:
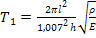 (41),
(41),
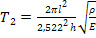 (42),
(42),
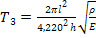 (43),
(43),
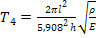 (44).
(44).
В зависимости от заданных физико-механических параметров биморфного элемента и величин, требуемых при расчете результатов, разработчик может пользоваться как формулами (25-28), (30-33), так и (37-40), (41-44).
Уравнение i-ой собственной формы составляем следующим образом.
Из первого или второго уравнения (23) находим, подставив туда kiℓ, значение отношения
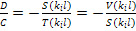 (45).
(45).
Подставив это значение в уравнение (22), получим
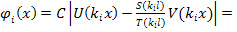
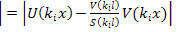 (46).
(46).
На рис. 3 представлены первые три формы поперечных колебаний биморфного элемента.
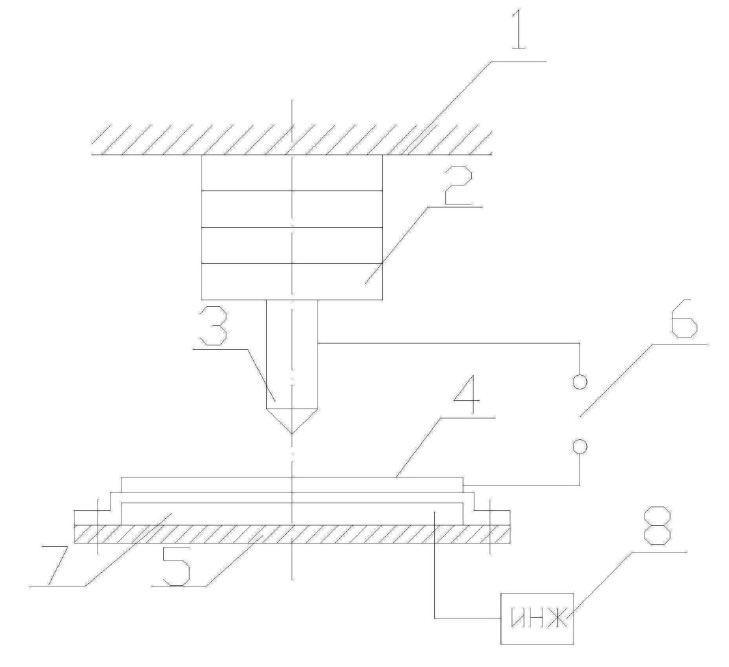
Рис. 3. Устройство формирования
квантовых точек из газовой среды
Для формирования квантовых точек на подложке могут использоваться и другие пьезмеханические системы. Одно из устройств формирования квантовых точек из газовой фазы, в котором превалирует роль продольных колебаний пьезопривода, представлено на рис. 4:
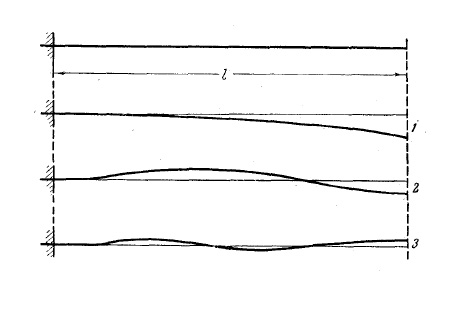
Рис. 4. Формы поперечных колебаний биморфного элемента
Устройство формирования квантовых точек из газовой среды, содержит неподвижное основание 1, установленный на нем пьезопривод 2 с зондом 3, электрически связанным с подложкой 4, установленной на подложкодержателе 5, источник гармонических колебаний напряжения 6, соединенный с зондом 3 и подложкой 4, подложкодержатель 5 выполнен с возможностью подачи внутрь полости 7 подложкодержателя 5 жидкого азота от источника жидкого азота 8.
Устройство для формирования квантовых точек из газовой среды работает следующим образом.
При перемещении зонда 3 посредством пьезопривода 2 относительно подложки 4 источник гармонических колебаний напряжения 6 посылает импульсы между зондом 3 и подложкой 4, в результате чего формируются квантовые точки из газовой среды, окружающей пространство между зондом 3 и подложкой 4. В это время происходит охлаждение подложки 4 путем подачи жидкого азота от источника жидкого азота (ИЖА) 8 в герметичную полость 7 внутри подложкодержателя 5, что приводит к уменьшению интенсивности процесса испарения материала с поверхности подложки 4 и его дрейфа.
На процесс формирования квантовых точек существенное влияние оказывает резонанс, возникающий в пьезоприводе.
Уравнения продольных колебаний биморфного элемента мы получим как необходимые условия экстремума функционалов (формула 47):
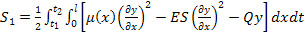
Интегралы по х, взятые в пределах от 0 до ℓ (ℓ – ширина биморфного элемента) от первого и двух последних слагаемых в квадратных скобках, представляют собой соответственно кинетическую и потенциальную энергию рассматриваемой системы.
Необходимое условие экстремума функционала S1 будет иметь вид:
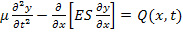 (48)
(48)
Условие (2) будет уравнением продольных колебаний.
Когда Q(x, t)≡0 и жесткость ES биморфного элемента постоянна по всей ширине биморфного элемента, то уравнение свободных колебаний однородного биморфного элемента имеет вид уравнения (11), где 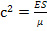 .
.
Уравнение собственных форм продольных колебаний будет иметь форму:
φ’’(x)+a2φ(x)=0 , (49) где 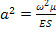 .
.
Задача о собственных формах и частотах колебаний приводится к интегрированию обыкновенных дифференциальных уравнений второго порядка с постоянными коэффициентами.
Частоты главных колебаний стержня образуют бесконечный дискретный ряд значений. Перенумерованные в порядке возрастания они вместе с порядковым номером растут до бесконечности.
Рассмотрим продольные колебания биморфного элемента с одним жестко закрепленным (х=0) и другим (х=ℓ) свободным концами.
В этом случае краевые условия выражаются равенствами: φ(0)=0, φ’(ℓ)=0.
Из этих условий находим значения постоянных B и D общего решения φ(x)=Bcosax+Dsinax.
Имеем: B=0, Dcosal=0.
Постоянная D не может, очевидно, равняться нулю, так как в противном случае φ(x)≡0. Нетривиальное решение получится при условииcosal=0, (50),(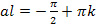 )
)
Из условия (50) находим:
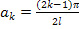 ;
;
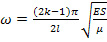 (k=1, 2, 3…) (51)
(k=1, 2, 3…) (51)
Таким образом, уравнение (50) отбирает собственные значения параметра а и вместе с тем определяет собственные частоты системы. Оно называется характеристическим уравнением или уравнением частот и соответствует вековому уравнению систем с конечным числом степеней свободы.
Учитывая (29) и (51), получим выражение для определения периода колебаний биморфного элемента:
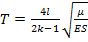 (52).
(52).
Характеристическое уравнение или уравнение частот можно получить в другом виде.
Определим площадь поверхности полого цилиндрического биморфного элемента: S=π(R2-r2) (53)
Учитывая формулы для вычисления массы m=ρV и объема V=ℓπ(R2-r2), получим выражение для погонной массы:
m=πρ(R2-r2) (54)
Стандартное выражение для вычисления частоты колебаний выглядит согласно формуле (16).
Подставляя в (51) вместо величин E, S и μ (53) и (54), имеем следующее выражение для определения частоты колебаний биморфного элемента:
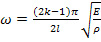 (55)
(55)
Величина, обратная частоте:
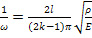 (56).
(56).
Учитывая выражения (29) и (54), получим окончательный вид уравнения периода колебаний биморфного элемента:
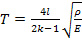 (57).
(57).
Разработчику можно пользоваться при расчетах формулами (29), (51), (55) и (57), в зависимости от заданных физико-механических параметров биморфного элемента и величин, которые необходимо рассчитать.
Применение предлагаемого устройства возбуждения кантилевера (рис. 2) позволяет расширить функциональные возможности устройства за счет использования схемы генератор магнитных колебаний – магнитная нанопластинка,. Применение предлагаемого устройства формирования квантовых точек из газовой среды (рис. 4) позволяет создавать квантовые точки с заданными промежутками между ними.



