Для обозначения аргумента используем первую букву английского слова price (цена), а первые буквы английских слов demand (спрос) и supply (предложение) для обозначения двух важных функций − функции спроса D = D(p) на некоторый товар и функции предложения S = S(p) этого товара. Количество товара – от английского quantity обозначим Q = Q(p). Если спрос на товар полностью удовлетворен, то выручка R(p) от продажи товара определяется по формуле R(p) = pD(p).
Пусть заданы функции
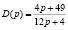
и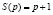 
. Построим их графики (рисунке).
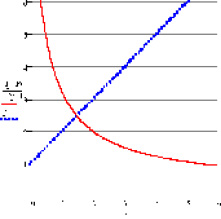
Найдём цену, при которой спрос и предложение уравновешиваются.
Равновесная цена определяется из условия: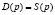 
, т. е. 
.
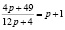Таким образом, получаем уравнение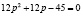 
. Отсюда находим равновесную цену 
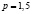и равновесный объём 
.
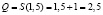Найдём эластичность по спросу и предложению:
.
.
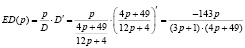
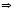
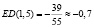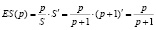
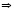
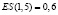Таким образом, при увеличении цены на 1 % спрос уменьшится на 0,7 %, a предложение увеличится на 0,6 %.
Найдём производную функции выручки:
,
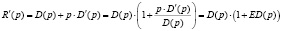где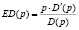 
.
В случае, когда ED(p) +1< 0, выручка является убывающей функцией от цены товара. Если ED(p) +1= 0, то выручка является постоянной функцией и от цены товара не зависит. Если же ED(p) +1> 0, то выручка является возрастающей функцией от цены товара.
Функцию D(p) называют эластичной в точке p, если в этой точке выполнено неравенство ED(p) >1. Если же в точке p выполнено неравенство ED(p) ≤1, то функцию D(p) называют неэластичной в точке p. Т. к.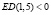 
, то спрос при цене 
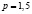не является эластичным.
При увеличении цены, например, на 15 % от равновесной: спрос уменьшится на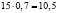 
%, доход продавца при этом возрастёт на 
%.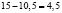