В работе решаем задачу. Три рабочих бригады должны выполнить демонтаж, установку и наладку водной турбины в машинном зале. Необходимо назначить бригады на работы методом динамического программирования, ветвей и границ так, чтобы затраты труда были минимальными.
Матрица затрат
|
7 |
7 |
2 |
|
3 |
9 |
5 |
|
4 |
5 |
4 |
Шаг 1. Затраты труда для выполнения демонтажа всеми бригадами:
|
i1 |
1 |
2 |
3 |
|
F1 |
6 |
3 |
4 |
Шаг 2. Сравнивя установку первой бригады со всеми остальными:
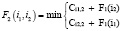 ,
,
Получаем
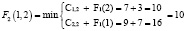 ;
;
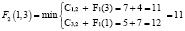 ;
;
Шаг 3. Сравниваем наладку первой бригады со всеми остальными:

И получаем:
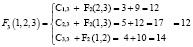 .
.
Минимальному значению соответствует С3,1, поэтому назначаем 3 бригаду на установку турбины. В обратную сторону: 1 бригада исполняет наладку турбины, 2 бригада – демонтаж турбины
Сделаем попытку назначить 1 бригаду на каждую работу. Для этого вычеркнем 1 строку и столбец в матрице затрат, в зависимости от того, на какую работу назначена бригада:
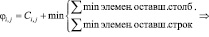
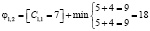
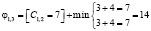
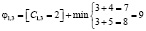
Так как минимальное значение достигается в случае φ1,3 = [C1,3 =2]=7, назначаем первую бригаду на наладку водной турбины. Остальные ветви 1 уровня отсекаем.
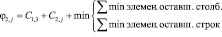
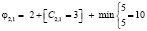
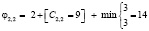
Минимальное значение φ2,1=10, поэтому назначаем вторую бригаду на демонтаж, а остальные ветви отсекаем.
Третья бригада назначается на оставшуюся работу, в данном случае, на установку турбины:
φ 3,2 = C1,3+ C2,1 + С3,3= 2+3+4=9.
Окончательный результат:
3 бригада – установка турбины
2 бригада – демонтаж турбины
1 бригада – наладка турбины



