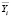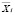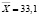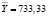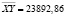Scientific journal
Modern high technologies
ISSN 1812-7320
"Перечень" ВАК
ИФ РИНЦ = 0,940

Personal portfolio

Svetlichnaya V.B. 1 Matveeva T.A. 1 1
1 Volzhsky Polytechnic Institute (branch) Volgograd State Technical University
Article in PDF
1023 KB

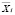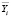Опытным путём были получены значения зависимостей интенсивности (авт/ч) и скорости (км/ч) автомобилей «ГАЗель». По этим значениям была составлена корреляционная таблица. Групповые средние (matm168.wmf и matm169.wmf) были включены в корреляционную таблицу (см. табл. 1).

Для установления корреляционного соотношения были вычислены вспомогательные величины (см. табл. 2).

Таблица 1

Значения зависимомостей

Скорость (X)

Интенсивность (Y)

300-400

400-500

500-600

600-700

700-800

800-900

900-1000

1000-1100

1100-1200

Всего ni

matm170.wmf

Середины

350

450

550

650

750

850

950

1050

1150

10-15

12,5

-

-

2

1

6

1

-

2

1

13

796,2

15-20

17,5

-

-

3

-

-

2

-

-

-

5

670

20-25

22,5

-

-

5

1

1

2

1

1

1

12

750

25-30

27,5

-

3

2

1

4

2

1

-

1

14

707,1

30-35

32,5

2

-

2

1

2

2

2

-

-

11

690,9

35-40

37,5

-

-

3

-

1

-

-

-

-

4

600

40-45

42,5

1

-

-

-

2

-

1

1

-

5

770

45-50

47,5

-

-

1

3

1

-

-

2

1

8

750,5

50-55

52,5

-

-

-

-

-

1

-

1

-

2

712

55-60

57,5

-

1

-

1

-

1

-

-

-

3

650

60-65

62,5

-

-

-

1

-

-

1

-

-

2

630

65-70

67,5

-

-

1

-

1

-

-

-

-

2

650

70-75

72,5

-

-

-

-

-

-

-

-

-

-

-

75-80

77,5

-

-

-

1

1

-

-

-

-

2

700

80-85

82,5

-

-

1

-

-

-

-

-

-

1

550

Всего ni

3

4

20

10

19

11

6

7

4

84

matm171.wmf

35,8

35

31

44

30,9

29,3

36,7

32,14

27,5

Таблица 2

Вспомогательные и основные величины

Среднее выборочное по X

matm172.wmf

Среднее выборочное по Y

matm173.wmf

Межгрупповая дисперсия по X

σх = 13,26

Межгрупповая дисперсия по Y

σy = 199,32

Межгрупповое среднее

matm174.wmf

Коэффициент корреляции

r = –0,144

Критерий Стьюдента

T = –1,318

Между величинами почти отсуствует линейная зависимость, что подтверждает критерий Стьюдента.

По расположению точек (Xi; Yxi) был установлен гиперболический вид линии регрессии.

Коэффициенты уравнения 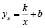matm175.wmf определены методом наименьших квадратов.

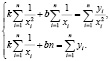
matm176.wmf

По расчётным данным получаем:

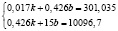
matm177.wmf

Решаем систему относительно k и b: k=2915,113; b=590,324.

Подставляем найденные коэффициенты в уравнение регрессии:

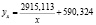matm178.wmf.

График теоретической линии регрессии и эмпирических точек (Xi ; Yxi) показаны на одном рисунке (см. рис. 1).

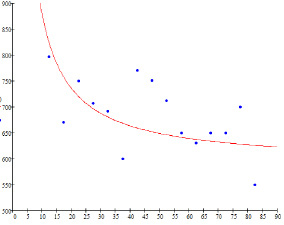
matmet14.tif

Рис. 1. График теоретической линии регрессии и эмпирических точек