В описании автоматических систем и их элементов используются линейные дифференциальные уравнения. Примером таких автоматических систем может служить функциональная схема автоматической системы управления курсом судна типа АИСТ с гидроприводом (ГП) руля. В работе показаны различные методы решения линейных дифференциальных уравнений.
Решим дифференциальное уравнение с начальными условиями операционным методом.
.
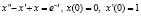Сущность метода состоит в том, что мы изучаем не саму функцию, а ее изображение по Лапласу. Перейдем к операторному преобразованию:
.
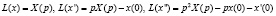Подставив начальные условия, получим уравнение: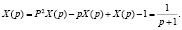 
Используя метод неопределенных коэффициентов, операторное решение уравнения представим в виде суммы простейших дробей:
.
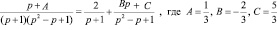По таблице преобразования Лапласа решение линейного дифференциального уравнения:
.
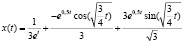Решим это же дифференциальное уравнения с помощью рядов.
.
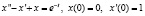Пусть частное решение это ДУ допускает разложение в степенной ряд Маклорена.
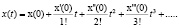
Вычисляем коэффициенты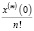 
, решение ДУ имеет вид:
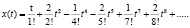
А еще представим решение линейного дифференциального уравнения в виде:
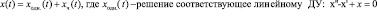
Корнями характеристического уравнения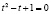 
являются комплексные числа
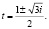
Следовательно,
.
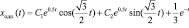Частное решение согласно функции e-t определяем по виду
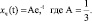
Из начальных условий коэффициенты
.
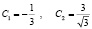Итак,
.
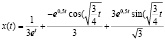В работе использованы три способа решения ЛНДУ. Ряды дают приближенное решение уравнения, два других способа определяют его точное решение.