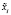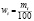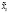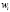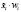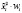В результате опыта получена выборочная совокупность (табл. 1).
Необходимо произвести статистическую обработку данной выборки.
Произведена сортировка данных по возрастанию. В результате можно составить интервальный вариационный ряд (табл. 2).
Следующим этапом обработки статистических данных является построение полигона, гистограммы относительных частот (рис. 1) и эмпирической функции распределения (рис. 2).
Таблица 1
|
21 |
13 |
28 |
19 |
20 |
14 |
24 |
23 |
18 |
15 |
32 |
14 |
15 |
20 |
16 |
18 |
14 |
22 |
21 |
24 |
|
7 |
22 |
17 |
17 |
26 |
22 |
21 |
21 |
14 |
23 |
24 |
18 |
25 |
18 |
20 |
21 |
20 |
22 |
7 |
31 |
|
18 |
14 |
22 |
17 |
5 |
20 |
20 |
11 |
17 |
19 |
19 |
3 |
15 |
16 |
19 |
7 |
25 |
13 |
20 |
15 |
|
16 |
12 |
19 |
16 |
16 |
22 |
21 |
7 |
14 |
21 |
20 |
26 |
17 |
14 |
14 |
14 |
10 |
26 |
12 |
9 |
|
12 |
11 |
15 |
19 |
13 |
15 |
2 |
6 |
21 |
9 |
23 |
16 |
16 |
21 |
11 |
14 |
19 |
19 |
28 |
12 |
Таблица 2
|
Интервал |
1,5-5,5 |
5,5-9,5 |
9,5-13,5 |
13,5-17,5 |
17,5-21,5 |
21,5-25,5 |
25,5-29,5 |
29,5-33,5 |
|
Середина интервала, |
3,5 |
7,5 |
11,5 |
15,5 |
19,5 |
23,5 |
27,5 |
31,5 |
|
Частота, mi |
3 |
7 |
11 |
28 |
30 |
14 |
5 |
2 |
|
Относительная частота, |
0,03 |
0,07 |
0,11 |
0,28 |
0,3 |
0,14 |
0,05 |
0,02 |
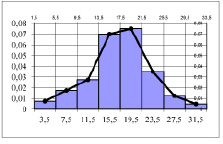
Рис. 1
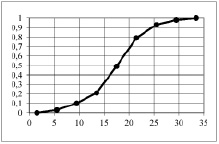
Рис. 2
Графики и соответствующие расчёты проведены в среде MS Excel.
Для нахождения выборочной средней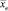 
, выборочной дисперсии Dв, выборочного среднего квадратического отклонения σв, заполняется вспомогательная табл. 3.
Выборочное среднее значение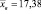 
, выборочная дисперсия определяется следующим образом: 
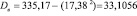. Тогда 
.
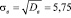Таблица 3
|
|
3,5 |
7,5 |
11,5 |
15,5 |
19,5 |
23,5 |
27,5 |
31,5 |
Σ |
|
|
0,03 |
0,07 |
0,11 |
0,28 |
0,3 |
0,14 |
0,05 |
0,02 |
1 |
|
|
0,11 |
0,53 |
1,27 |
4,34 |
5,85 |
3,29 |
1,38 |
0,63 |
17,38 |
|
|
0,37 |
3,94 |
14,55 |
67,27 |
114,08 |
77,32 |
37,81 |
19,85 |
335,17 |
Вид гистограммы относительных частот напоминает график функции плотности нормального распределения с параметрам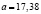и: 
и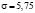 
. Строим его на одном чертеже с гистограммой относительных частот (рис. 3). Используя встроенную функцию MS Excel НОРМРАСП() можно построить интегральную функцию нормального распределения на одном графике с эмпирической функцией (рис. 4).
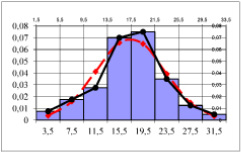
Рис. 3
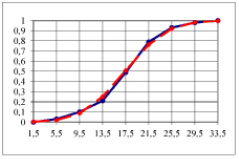
Рис. 4