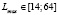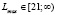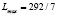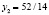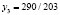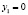Каждый студент задаётся вопросом: «Для чего нужно линейное программирование и понадобится ли оно мне в жизни?» Рассмотрим значимость данной математической дисциплины с точки зрения бизнеса и производства.
Прибегая к линейному программированию, производитель может найти оптимальный производственный план, благодаря которому будет достигаться максимум прибыли при минимуме издержек, а также проследить за тем, как будет изменяться прибыль при изменении величины ресурсов. Приведём пример.
У нас есть следующая функция:
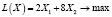 ,
,
с её ограничениями: 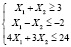
Сделаем анализ устойчивости. График нашей функции будет выглядеть следующим образом:
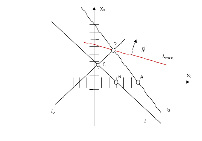
Интересующая нас область является фигурой ABCD.
После изменения коэффициентов целевой функции и анализа изменений констант в правой части неравенств ограничений мы получим стоимость ресурсов, которая выглядит следующим образом:
|
Стоимость ресурсов |
||
|
Дефицитные ресурсы |
Недефицитные ресурсы |
|
|
b2 |
b3 |
b1 |
|
Интервал устойчивости |
||
|
[-8;6] |
[9,5;∞) |
[0;50/7] |
|
Оптимальное значение целевой функции |
||
|
|
|
|
|
Мера устойчивости (условная стоимость) |
||
|
|
|
|
В итоге, мы получаем следующий вывод: максимальное значение L равно 292/7, достигающееся при величинах 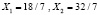 .
.
Интервалы устойчивости активных запасов:
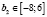 ;
; 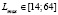
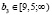 ;
; 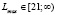
Пассивных запасов:
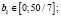
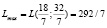
Стоимость ресурсов:
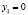 ;
; 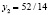 ;
; 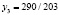 .
.
С учётом проведения анализа устойчивости, производитель будет производить продукцию на основании полученного плана, что, несомненно, будет положительно сказываться на его ведении дел.