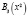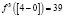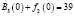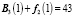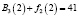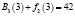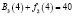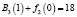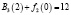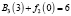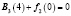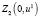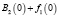Динамическое программирование – это математический метод поиска оптимального управления, специально приспособленный к многошаговым процессам. Ключевая идея динамического программирования заключается в нахождении оптимального решения подзадач меньшего размера с дальнейшим объединением в одно общее решение. Метод позволяет достичь существенной экономии вычислений по сравнению с полным перебором вариантов.
Реализацию метода динамического программирования рассмотрим на примере решения следующей дискретной задачи.
Для подготовки к трем зачетам по дисциплинам: теоретическая механика, математика и английский язык студенту предоставлено 4 дня. Зависимость получения баллов на зачете от количества затраченных на подготовку дней представлены в табл. 1. Необходимо определить стратегию подготовки к трем зачетам, так чтобы получить максимальную сумму баллов.
Таблица 1
Зависимость количества баллов от затраченных на подготовку дней
|
Количество баллов, fk(u) |
Выделенные дни на подготовку к зачетам, u |
||||
|
0 |
1 |
2 |
3 |
4 |
|
|
f1(u) |
0 |
10 |
17 |
21 |
38 |
|
f2(u) |
0 |
25 |
29 |
36 |
40 |
|
f3(u) |
0 |
6 |
12 |
18 |
39 |
Для решения задачи сформулируем многошаговую математическую модель: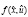 
– Целевая функция задачи (максимальное количество баллов), где 
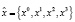– оставшееся количество дней (xk) после k-го выученного предмета (фазовая траектория), 
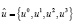– количество дней (uk) затраченных на k-й зачет (вектор управлений).
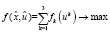
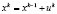– уравнение состояний, xk∈[0;4] и uk ∈[0;4–xk-1].
Рассмотрим реализацию метода динамического программирования:
Этап 1. (условная оптимизация).
Шаг 1. Найдем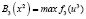 
– функция Беллмана. Так как 
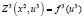есть возрастающая функция аргумента u3 (по табл. 1), то её максимум достигается при максимально допустимом значении u3, т.е. 
.
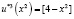Отсюда,
.
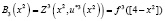Значения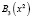 
, найдем с помощью табл. 1.
Таблица 2
Значения функции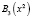 
|
x2 |
0 |
1 |
2 |
3 |
4 |
|
|
|
18 |
12 |
6 |
0 |
Шаг 2. Найдем
.
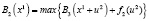Для определения максимума функции
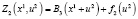
составим табл. 3, используя табл. 1 и 2.
Таблица 3
Значения функции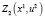 
|
x1 |
u2 |
0 |
1 |
2 |
3 |
4 |
|
0 |
|
|
|
|
|
|
|
1 |
|
37 |
35 |
36 |
- |
|
|
2 |
|
31 |
29 |
- |
- |
|
|
3 |
|
25 |
- |
- |
- |
|
|
4 |
|
- |
- |
- |
- |
|
В табл. 3 жирным шрифтом выделены максимальные по u2 значения функции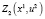 
, соответствующие различным x1. С помощью табл. 3 находим значения функции 
.
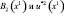Таблица 4
Значения функции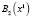 
|
x1 |
0 |
1 |
2 |
3 |
4 |
|
43 |
37 |
31 |
25 |
0 |
Таблица 5
Значения функции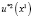 
|
x1 |
0 |
1 |
2 |
3 |
4 |
|
1 |
1 |
1 |
1 |
0 |
Шаг 3. Найдем
,
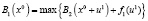где x0=0. Для определения максимума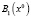 
составим табл. 6 значений функции
,
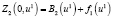которые найдем с помощью табл. 1 и 4.
Таблица 6
Значения функции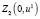 
|
u1 |
0 |
1 |
2 |
3 |
4 |
|
|
|
47 |
48 |
46 |
40 |
Из таблицы следует, что u*1(0)=2; B1(0)=48.
Этап 2. (безусловная оптимизация).
Шаг 0. Оптимальное начало фазовой траектории определяется начальным условием х*0=0.
Шаг 1. С помощью таблицы находим
u*1= u*1(0)=2; x*1=x*0+u*1=0+2=2.
Шаг 2. Из таблицы 5 получаем
u*2= u*2(2)=1; х*2=х*1+u*2=2+1=3.
Шаг 3. u*3=u*3(x*2)=u*3(3)=1; x*3=x*2+u*3=3+1=4.
В результате проведенных расчетов получаем: количество дней затраченных на 1-2-3 зачет соответственно, при этом максимальное суммарное количество баллов составляет B1(0)=48 баллов.