Под упорядочиваемой группой понимаем группу, допускающую линейное упорядочение.
Подгруппа упорядочиваемой группы называется относительно выпуклой, если она выпукла при некотором линейном порядке группы.
Подгруппу, выпуклую при любом линейном порядке группы, называем абсолютно выпуклой. Подгруппа H группы G называется строго изолированной, если из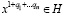 
следует 
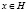где 
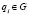. Наименьшая из строгого изолированных подгрупп, содержащих данное множество, называется строгим изолятором этого множества.
Как обычно, через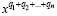 
обозначается произведение сопряженных 
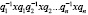, а через g(A) – ценрализатор A в G. Модулем над ассоциативным кольцом K называется, абелева группа M, на которой действует кольцо операторов K с единицей e, причем выполняется следующие аксиомы:
,
,
,
,
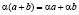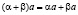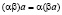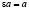где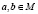 
, 
.
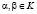Линейно упорядоченным модулем M над линейно упорядоченным кольцом K называется K – модуль, в котором введено отношение линейного порядка £, превращающее M в линейно упорядоченную группу и устойчивое относительно умножения на положительные элементы кольца операторов ...
Модуль M с упорядоченным кольцом R в качестве области операторов называем упорядочиваемым, если он допускает линейное упорядочение, как абелева группа, при котором для каждого неотрицательно элемента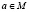 
и каждого неотрицательного элемента 
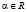также и aa неотрицательно.
Упорядочиваемые модули играют важную роль в теории упорядочиваемых групп.
В дальнейших рассуждениях нам потребуется следующее утверждение: Если B – упорядочиваемый модуль над целочисленным групповым кольцом zG упорядочиваемой абелевой группы G и f – совокупность таких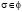 
, что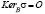 
, то B вкладывается в такой упорядочиваемый zG – модуль B*, что каждое s из f есть автоморфизм B*; для всякого 
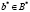найдется такое 
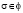, что b*s лежит в B.
В работах [1] и [2] с использованием упорядоченных модулей доказана следующая теорема:
Теорема 1. Пересечение всех относительно выпуклых подгрупп упорядочиваемой группы является абсолютно выпуклой подгруппой этой группы.
Возникает вопрос, как «богат» класс упорядочиваемых подгрупп, имеющих неотрицательное пересечение всех своих относительно выпуклых подгрупп. Ответом на поставленный вопрос служит следующая теорема:
Теорема 2. Пересечение всех относительно выпуклых подгрупп упорядочиваемой группы G не является единицей в том и только в том случае, если выполняются следующие три условия:
В G имеется инвариантная абелева подгруппа A;
G/g(A) – абелева (g(A) – централизатор AbG).
Всякое отражени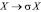е 
, где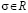 
подкольцу поля действительных чисел, порожденному группой G/g(A) 
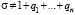– есть автоморфизм.