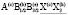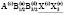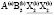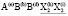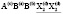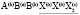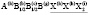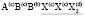Структура шпинели была установлена независимо Брэггом (W.Н. Bragg) [1] и Нишикавой (S. Nishikawa) [2] почти сто лет назад в 1915 году. Но вещества с этой структурой представляют и в настоящее время интерес для широкого круга химиков, физиков, минералогов, металлургов и материаловедов. Многие свойства шпинелей существенно зависят от упорядочения атомов в их структуре [3-16], в том числе и в анионной подрешетке [17-19]. Целью данного исследования является полное решение задачи о перечислении возможных типов порядка в анионной подрешетке структуры шпинели. Нами использован теоретико-групповой метод термодинамической теории фазовых переходов, детально описанный в [20-32].
Представление упорядочения, построенное на позиции 32(e) структуры шпинели имеет размерность 80. Разложение этого представления на неприводимые преставления имеет следующий вид
k8(τ1+τ2) + k9(2τ1+2t4+t5+t6) +k10(τ1+2τ3+t4)+k11(τ1(A1g) + t4(A2u)+ t7(F2g)+τ10(F1u)). (1)
Обозначения волновых векторов и неприводимых представления даны по книге О.В. Ковалева [33]. Симметрийный анализ параметра порядка (ПП) (1) с учетом единичного представления предсказывает 358 низкосимметричных упорядоченных фаз. Как видно из таблицы, среди этих фаз имеется 7 бинарных (фазы 1-7) и 4 тройных (фазы 8-11) сверхструктур. Причем двойные и тройные сверхструктуры возможны с одним ПП, преобразующимся по одному неприводимому представлению. Упорядочение в бинарных сверхструктурах происходит по типам 1:1 и 1:3, а в тройных – только по типам 1:1:2.
Неприводимые представления с волновым вектором k8 не генерируют бинарных и тройных анионных сверхструктур. Отметим, что среди бинарных сверхструктур имеются три пары энантиоморфных модификаций упорядоченных шпинелей.
Наиболее распространенными типами анионного упорядочения в позициях 32(e) структуры шпинели являются структуры с пространственными группами 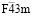 ((параметр порядка (x), k11t4),
((параметр порядка (x), k11t4), 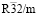 ((параметр порядка x, -x, x), k11t7) и энантиоморфными группами P41,3212 (параметр порядка (0, 0, j, 0, 0, 0), k10τ2).
((параметр порядка x, -x, x), k11t7) и энантиоморфными группами P41,3212 (параметр порядка (0, 0, j, 0, 0, 0), k10τ2).
Структура упорядоченной шпинели с пространственной группой 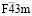 . Выше мы уже рассмотрели структуру
. Выше мы уже рассмотрели структуру 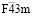 –фазы, имеющей формулу A`4(a)A4(a)B16(e)4X416(e)X`416(e). Частным случаем структур упорядоченных шпинелей можно рассматривать структуру фаз Шевреля. Структуру этих фаз можно представить как структуру дефектных шпинелей с упорядочением тетраэдрических катионов и анионов типа 1:1. Если отсутствуют все или только некоторые из атомов A`4(a) и A`4(a), то получаются различные типы фаз Шевреля [34, 35]. Так, например, если на позициях 4(а) нет атомов A`4(a) и A`4(a) , то тогда получим структурную формулу B16(e)4X416(e)X`416(e). Эта формула отражает строение Re4Te4S4 [36, 37]. Если отсутствует только один тип атомов А, тогда получим A4(a)B16(e)4X416(e)X`416(e). Такую структурную формулу имеют GaMo4O8 [35] и Re4As6S3 [38]. Если частично заняты позиции атомов A`4(a) и A`4(a), то тогда получаются структурные формулы веществ, подобных Ga1,33Cr4S8 [35] и Ga0.5V2S2Se2 [39].
–фазы, имеющей формулу A`4(a)A4(a)B16(e)4X416(e)X`416(e). Частным случаем структур упорядоченных шпинелей можно рассматривать структуру фаз Шевреля. Структуру этих фаз можно представить как структуру дефектных шпинелей с упорядочением тетраэдрических катионов и анионов типа 1:1. Если отсутствуют все или только некоторые из атомов A`4(a) и A`4(a), то получаются различные типы фаз Шевреля [34, 35]. Так, например, если на позициях 4(а) нет атомов A`4(a) и A`4(a) , то тогда получим структурную формулу B16(e)4X416(e)X`416(e). Эта формула отражает строение Re4Te4S4 [36, 37]. Если отсутствует только один тип атомов А, тогда получим A4(a)B16(e)4X416(e)X`416(e). Такую структурную формулу имеют GaMo4O8 [35] и Re4As6S3 [38]. Если частично заняты позиции атомов A`4(a) и A`4(a), то тогда получаются структурные формулы веществ, подобных Ga1,33Cr4S8 [35] и Ga0.5V2S2Se2 [39].
Бинарное и тройное катионное упорядочение в вайковой позиции 32(e) структуры шпинели 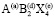
|
№ п/п |
Параметры порядка |
Символ пространственной группы |
V’/V |
Трансляции примитивной ячейки |
Структурная формула |
|
1 |
(0, x, 0)10 |
C4v11=I41md(N109) |
1 |
a1, a2, a3 |
|
|
2 |
(x)4 |
Td2= |
1 |
a1, a2, a3 |
|
|
3 |
(x, -x, x)7 |
D3d5= |
1 |
a1, a2, a3 |
|
|
4 |
(0, j, 0, j, 0, -j)1 |
O6=P4332(N212) O7=P4132(N213) |
4 |
a1+a2+a3, 2a2, 2a1 |
|
|
5 |
(0, 0, j, 0, 0, 0)2 |
D44=P41212(N92) D48=P43212(N96) |
2 |
a1+a3, a2, 2a1 |
|
|
6 |
(0, 0, x)7 |
D2h28=Ibmm(N74) |
1 |
a1, a2, a3 |
|
|
7 |
(0, j, 0, 0, 0, 0)1 |
D43=P4122(N91) D47=P4322(N95) |
2 |
a1+a2, 2a1, a3 |
|
|
8 |
(x, -x, 0)10 (0, 0, x)7sec. |
C2v22=Ima2(N46) |
1 |
a1, a2, a3 |
|
|
9 |
(j, -j, 0, 0, 0, 0)1 (0, 0, x)7sec. |
D2h7=Pbmn(N53) |
2 |
a1+a2, a3, 2a1 |
|
|
10 |
(j, j, 0, 0, 0, 0)2 (0, 0, x)7sec. |
D2h16=Pbnm(N62) |
2 |
a1+a2, a3, 2a1 |
|
|
11 |
(ξ1, ξ2, -ξ1)7 |
C2h3=C2/m(N12) |
1 |
a1, a2, a3 |
|
Примечание. Обозначения для ПП: k8 – q, k9 – h; k10 – j, k11 – x. Верхний индекс после круглой скобки – номер представления по Ковалеву [33], V’/V – изменение объема примитивной ячейки в результате структурного фазового превращения. Верхний индекс в стехиометрической формуле – обозначение типа позиции по интернациональным таблицам.
Структура фаз Шевреля, их свойства и особенности строения генетически связаны со строением упорядоченных шпинелей. В частности, при упорядочении катионов типа 1:1 в тетраэдрических узлах шпинели AB2X4 образуются кластеры B4 из металлических атомов и анионов [30]. Структура фаз Шевреля «наследует» из структуры упорядоченной шпинели четыре типа кластеров, которые были установлены в результате теоретического исследования структурного механизма образования упорядоченной шпинели с F 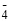 3m – симметрией [30]. Мы полагаем, что образование именно этих кластеров и обуславливает своеобразие физических свойств фаз Шевреля. Кластеры рения Re4 существуют в фазах Шевреля с составами Re4As6S3, Re4Te4S4.
3m – симметрией [30]. Мы полагаем, что образование именно этих кластеров и обуславливает своеобразие физических свойств фаз Шевреля. Кластеры рения Re4 существуют в фазах Шевреля с составами Re4As6S3, Re4Te4S4.
Структура упорядоченной шпинели с пространственной группой 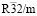 . Эта структура генерируется НП k11t7. Это НП входит в механическое представление структуры шпинели на позициях 8(a) и 32(e) и в перестановочное представление на позициях 16(d) и 32(e). Это означает, образование низкосимметричной фазы происходит в результате смещений тетраэдрических атомов и анионов, а также упорядочений октаэдрических катионов и анионов (тип порядка в обоих случаях 1:3). Структурная формула вещества должна быть A2(c)B1(a)1/2B3(d)3/2X2(c)X6(h)3. На рис. показаны особенности строения
. Эта структура генерируется НП k11t7. Это НП входит в механическое представление структуры шпинели на позициях 8(a) и 32(e) и в перестановочное представление на позициях 16(d) и 32(e). Это означает, образование низкосимметричной фазы происходит в результате смещений тетраэдрических атомов и анионов, а также упорядочений октаэдрических катионов и анионов (тип порядка в обоих случаях 1:3). Структурная формула вещества должна быть A2(c)B1(a)1/2B3(d)3/2X2(c)X6(h)3. На рис. показаны особенности строения 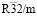 -фаз. Рассмотренную структуру, по-видимому, имеет Ga3O3N, обладающий перспективными электронными свойствами [40]. Авторы [40] рассмотрели три модели строения оксинитрида галлия, описываемых пространственными группами Ima2, Imm2 и
-фаз. Рассмотренную структуру, по-видимому, имеет Ga3O3N, обладающий перспективными электронными свойствами [40]. Авторы [40] рассмотрели три модели строения оксинитрида галлия, описываемых пространственными группами Ima2, Imm2 и 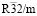 . Исследования локальной электронной структуры позволили авторам этой работы установить упорядоченное расположение анионов и выбрать модель строения Ga3O3N с пространственной группой
. Исследования локальной электронной структуры позволили авторам этой работы установить упорядоченное расположение анионов и выбрать модель строения Ga3O3N с пространственной группой 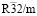 . Необходимо отметить, что при образовании
. Необходимо отметить, что при образовании 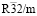 -фазы Ga3O3N происходит не только упорядочение кислорода и азота, но и упорядочение двух из трех атомов галлия, занимающих позиции 1(a) и 3(d).
-фазы Ga3O3N происходит не только упорядочение кислорода и азота, но и упорядочение двух из трех атомов галлия, занимающих позиции 1(a) и 3(d).
Структура упорядоченной шпинели с пространственной группой P41,3212. Критическим НП, индуцирующим образование P41,3212-фаз, является шестимерное представление звезды k10(τ2).
Анализ показывает, что структура такой фазы формируется в результате смещений всех типов атомов, а также упорядочения атомов, находящихся в позиции 32(e) (тип порядка 1:1). Структурная формула упорядоченной шпинели: A4(a)B8(b)2X8(b)2X8(b)2.
Примером подобной структуры является структура MgTi2O4 [41, 42]. В этом веществе при температуре ~260 К происходит фазовый переход, сопровождающийся изменением типа проводимости (металл–изолятор), значительным уменьшением магнитной восприимчивости, перестройкой структуры: кубическая шпинель (пр. гр. Fd3m) превращается в тетрагональную модификацию (пр. гр. P41212 или энантиоморфная ей P43212) [41, 42]. В [42] отмечается существование на нейтронограммах и рентгенограммах слабых сверхструктурных рефлексов. Их появление обусловлено, согласно нашим расчетам, упорядочением ионов кислорода [43, 44]. Вайковые позиции 32(е), в которой находятся атомы кислорода в исходной кубической шпинели, в результате фазового перехода расслаивается на две вайковые позиции с одинаковой локальной симметрией 1(С1) и одинаковыми кратностями. Это означает, что упорядочение кислорода действительно происходит по типу 1:1, как и предсказывает теория. В работе [43] предложена теория фазового перехода в MgTi2O4: проведено исследование симметрии параметра порядка, термодинамики и механизмов образования атомной и орбитальной структуры низкосимметричной фазы MgTi2O4.
Результаты работы получены при поддержке Минобрнауки РФ в рамках государственного задания на проведение НИОКР, шифр заявки N6.8604.2013.




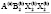
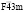 (N216)
(N216)
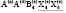
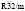 (N166)
(N166)