Решение задачи определения возможных сверхструктур в шпинелях представляет значительный научный и практический интерес. Образование сверхструктур сопровождается появлением у вещества качественно новых физических и химических свойств и, прежде всего, магнитных, упругих, оптических и электрических. Так, например, упорядочение катионов сопровождается образованием новых подрешеток в кристалле, которые способствуют возникновению ферримагнетизма (ферримагнетики с наведенным ферримагнетизмом [1]). Примером может быть шпинель Cu+[Ni1/2+2Mn3/2+4]O4 с упорядоченным распределением катионов в октаэдрических узлах [1]. Низкотемпературный фазовый переход в упорядоченную фазу в магнетите сопровождается аномалией удельной теплоемкости, изменением проводимости приблизительно на два порядка и изменением знака магнитной кристаллографической анизотропии [2]. У хлоридных шпинелей вблизи температуры упорядочения обнаружена, в частности, аномально высокая суперионная проводимость [3-5].
Целью данного исследования является решение задачи о перечислении возможных сверхструктур, возникающих в результате одновременного упорядочения катионов в тетраэдрических и октаэдрических позициях структуры шпинели. Нами рассмотрены случаи одновременного упорядочения в двух катионных подрешетках структуры шпинели. Особенность структуры шпинели состоит в том, что различные катионы могут перераспределяться между вайковыми позициями 8(a) и 16(d). Это означает, что возможно упорядочение не только по одному, но и по двум параметрам порядка одновременно. Такие расчеты ранее не проводились. Нами использован теоретико-групповой метод термодинамической теории фазовых переходов, детально описанный в [6-19]. Этот метод позволяет получить список возможных сверхструктур без привлечения каких бы то ни было модельных соображений.
Представление упорядочения, построенное на позициях 8(а) и 16(d), имеет размерность 52. Разложение этого представления на неприводимые преставления имеет вид:
k8(τ1+τ2) + k9(τ1+t4+t5) + k10(τ1+τ3) + k11(t4(A2u) + t7(F2g)) (1)
Обозначения волновых векторов и неприводимых представления даны по книге О.В. Ковалева [19]. Анализ параметра порядка (1) без учета единичного представления предсказывает 330 низкосимметричную упорядоченную фазу. Как видно из таблицы среди этих фаз имеется пять фаз с бинарным порядком в тетра- и октаэдрических подрешетках шпинели двух типов (1:1)8(а)[1:3]16(d) и (1:1)8(а)[1:1]16(d), шесть фаз с бинарным и тройным порядками трех типов (1:1)8(а)[1:1:6]16(d), (1:1)8(а)[2:3:3]16(d) и (1:1)8(а)[1:1:2]16(d), три фазы с тройным и бинарным порядками двух типов (1:3:4)8(а)[1:3]16(d) и (1:1:2)8(а)[1:1]16(d), две фазы с тройным порядками в обеих подрешетках двух типов (1:1:2)8(а)[2:2:1]16(d) и (1:1:2)8(а)[1:1:2]16(d). В таблице приняты обозначения такие же как и в таблицах данной мери публикаций.
Известен один тип сверхструктур с одновременным упорядочением катионов в позициях 8(а) и 16(d) структуры шпинели: упорядоченная фаза LiZn0,5Mn1,5O4 с пространственной группой P213. Эта фаза образована двумя параметрами порядка (x)4 и (0, j, 0, j, 0, -j)1. Эти неприводимые представления образуют точечную группу 192 порядка в семимерном пространстве. Структурный механизм образования исследуемой низкосимметричной фазы по представлению k10(τ3) + k11(t4) оказывается сложным и включает:
– бинарные упорядочения катионов типа 1:1 в тетраэдрических узлах 8(а) и типа 1:3 в октаэдрических позициях 16(d) шпинели;
– четверное упорядочение анионов типа 1:1:3:3 в структуре исходной фазы;
– смещения всех типов атомов.
Отметим, что данный структурный механизм образования P213-фазы значительно сложнее, чем предполагался ранее для LiZn0,5Mn1,5O4 [20]: он не сводится только к упорядочению лития, цинка и марганца. Расчетная структурная формула P213-фазы имеет вид: (A4(а)1/2A`4(а)1/2)[B4(а)1/2B`12(b)3/2]Х12(b)Х12(b)Х4(а)Х4(а). Экспериментальные данные по строению LiZn0,5Mn1,5O4, полученные с помощью нейтронографического и рентгеноструктурного анализов, согласуются со структурной формулой [20]. В нашей работе [21] детально рассмотрено строение этой фазы.
Одновременное бинарное и тройное катионное упорядочение в вайковых позициях 8(a) и 16(d) структуры шпинели 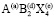
|
№ п/п |
Параметры порядка |
Символ пространственной группы |
V´/V |
Трансляции примитивной ячейки |
Структурная формула |
|
1 |
(0, j, 0, j, 0, -j)3,A,B (x)4,Asec. |
Td1= |
4 |
a1+a2+a3, 2a2, 2a1 |
|
|
2 |
(0, 0, h, 0)4,A (x, -x, x)7,B |
D3d5= |
2 |
a1, a3, 2a2 |
|
|
3 |
(0, 0, h, 0)1,A,B (x, -x, x)7,Bsec. |
D3d5= |
2 |
a1, a3, 2a2 |
|
|
4 |
(0, j, 0, 0, 0, 0)3,A,B (x)4,Asec. |
D2d5= |
2 |
a1+a2, a3, 2a1 |
|
|
5 |
(j, 0, 0, 0, 0, -j)3,A,B (0, 0, j, 0, 0, 0)1,Bsec. |
D43=P4122(N91) D47=P4322(N95) |
4 |
a1+a2+a3, 2a2, 2a3 |
|
|
6 |
(j, j, 0, 0, 0, 0)3A,B (0, 0, x)7,Bsec. |
D2h5=Pcmm(N51) |
2 |
a2+a3, a1, 2a2 |
|
|
7 |
(0, j, 0, 0, j, 0)1,B (x)4,A (0, 0, 0, j, 0, 0)3,A,Bsec. |
D2d3= |
4 |
a1+a2+a3, 2a2, 2a1 |
|
|
8 |
(x)4,A (x, -x, x)7,B |
C3v5=R3m(N160) |
1 |
a1, a2, a3 |
|
|
9 |
(x)4,A (0, x, 0)7,B |
C2v20=Imm2(N44) |
1 |
a1, a2, a3 |
|
|
10 |
(x)4,A (0, j, 0, j, 0, -j)1,B |
T4=P213(N198) |
4 |
a1+a2+a3, 2a2, 2a1 |
|
|
11 |
(x)4,A (0, 0, 0, 0, 0, j)1,B |
D25=C2221(N20) |
2 |
a2+a3, 2a2, a1 |
|
|
12 |
(x)4,A (0, 0, j, j, 0, 0)1,B (0, x, 0)7,B sec. |
C2v7=Pmn21(N31) |
2 |
a1+a3, a2, 2a1 |
|
|
13 |
(x)4,A (ξ1, -ξ1, ξ2)7,B |
Cs3=Cm(N8) |
1 |
a1, a2, a3 |
|
|
14 |
(0, 0, q, q, 0, 0, 0, 0, 0, 0, 0, 0)1,A,B (x)4,A sec. |
D2d12= |
4 |
a1+a2-a3, 2a2, a1+a3 |
|
|
15 |
(0, q, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)2,B (x)4,A (0, j, 0, 0, 0, 0)3,A,Bsec. |
D2d11= |
4 |
a1+a2-a3, 2a2, a1+a3 |
|
|
16 |
(0, 0, q, q, 0, 0, 0, 0, 0, 0, 0, 0)2,B (x)4,A |
D2d12= |
4 |
a1+a2-a3, 2a2, a1+a3 |
|
Результаты работы получены при поддержке Минобрнауки РФ в рамках государственного задания на проведение НИОКР, шифр заявки N6.8604.2013.




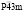 (N215)
(N215)
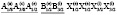
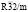 (N166)
(N166)
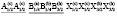
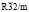 (N166)
(N166)
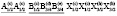
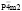 (N115)
(N115)
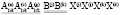
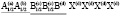

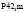 (N113)
(N113)
 (N122)
(N122)
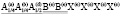
 (N121)
(N121)
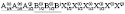
 (N122)
(N122)