Теория краевых задач для уравнений смешанного типа является одним из важнейших разделов теории дифференциальных уравнений с частными производными, что объясняется как теоретической значимостью результатов, так и их приложениями в газовой динамике, в теории бесконечно малых изгибаний поверхностей, в безмоментной теории оболочек, в магнитной гидродинамике, в математической биологии и других областях.
В настоящее время теория уравнений смешанного типа развивается быстрыми темпами. Успехи современного естествознания требуют дальнейшего развития теории дифференциальных уравнений в частных производных, что приводит к необходимости исследования локальных и нелокальных краевых задач, в том числе задач со смещением для уравнений смешанного и смешанно – составного типов.
Цель исследования: доказать существование и единственность решения задачи типа задачи Бицадзе-Самарского для уравнения смешанного гиперболо – параболического типа.
Постановка задачи. Рассмотрим уравнение
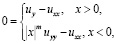 (1)
(1)
где 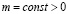 , в конечной области D, ограниченной отрезками CD, OD, DC прямых
, в конечной области D, ограниченной отрезками CD, OD, DC прямых 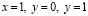 и характеристиками
и характеристиками 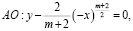
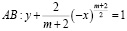 уравнения (1) при
уравнения (1) при 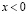 .
.
Пусть 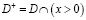 ,
, 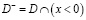 ,
, 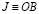 – единичный интервал
– единичный интервал 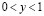 прямой
прямой 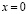 .
.
Под регулярным решением уравнения (1) будем понимать функцию 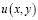 из класса
из класса 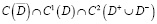 , удовлетворяющую уравнению (1) в
, удовлетворяющую уравнению (1) в 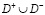 и такую, что
и такую, что 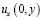 на концах интервала J может обращаться в бесконечность порядка
на концах интервала J может обращаться в бесконечность порядка 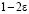 , где
, где 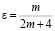 .
.
Задача. Найти регулярное решение уравнения (1), удовлетворяющее условиям
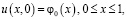 (2)
(2)
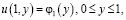 (3)
(3)
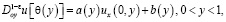 (4)
(4)
где 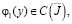
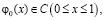
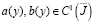 ;
; 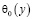 – точка пересечения характеристики, выходящей из точки
– точка пересечения характеристики, выходящей из точки 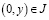 , с характеристикой AO;
, с характеристикой AO; 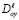 – оператор дробного интегро-дифференцирования в смысле Римана-Лиувилля, определяемый по формуле [10]
– оператор дробного интегро-дифференцирования в смысле Римана-Лиувилля, определяемый по формуле [10]
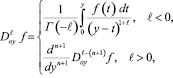
где 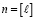 ,
, 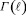 – гамма-функция.
– гамма-функция.
Задача (1) – (4) относится к классу краевых задач со смещением [7], исследованием которых занимались многие авторы [1-9] для уравнений смешанного типа. Интерес к таким задачам обусловлен тем, что они существенно обобщают задачу Трикоми, содержат широкий класс корректных самосопряженных задач и имеют многомерные аналоги.
Пусть 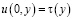 ,
, 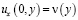 . Тогда решение задачи Коши в области D– представимо в виде [7]
. Тогда решение задачи Коши в области D– представимо в виде [7]
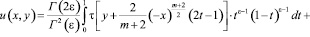
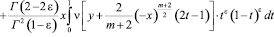 . (5)
. (5)
Удовлетворив
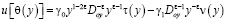 ,
,
где 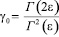 ,
, 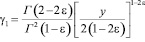 ,
,
условию (4), получим основное функциональное соотношение между 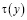 и
и 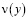 , принесенное из гиперболической части D– на J
, принесенное из гиперболической части D– на J
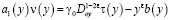 ,
,
где 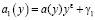 , или, что тоже самое,
, или, что тоже самое,
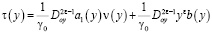 . (6)
. (6)
Для нахождения функционального соотношения между 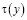 и
и 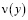 , принесенного из D+ на J рассмотрим задачу: Найти регулярное решение уравнения (1) при
, принесенного из D+ на J рассмотрим задачу: Найти регулярное решение уравнения (1) при 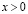 , удовлетворяющее условиям (2)-(3),
, удовлетворяющее условиям (2)-(3), 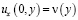 .
.
Известно [9], что решение этой задачи существует, единственно и дается формулой
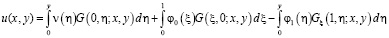 ,
,
где 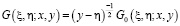 – функция Грина;
– функция Грина;
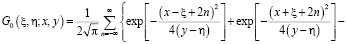
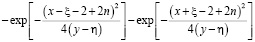 . (8)
. (8)
Отсюда второе функциональное соотношение между 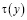 и
и 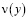 , принесенное из D+ на J имеет вид
, принесенное из D+ на J имеет вид
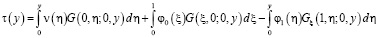
или
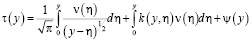 , (9)
, (9)
где
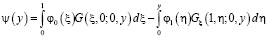 ,
,
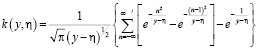 .
.
Знак 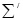 означает, что в сумме отсутствует слагаемое, соответствующее значению n=0.
означает, что в сумме отсутствует слагаемое, соответствующее значению n=0.
Подставляя 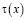 из (6) в (9), получим уравнение относительно
из (6) в (9), получим уравнение относительно 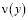
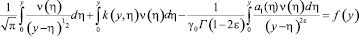 ,
,
где
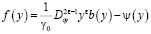 .
.
Отсюда, применив формулу обращения интегрального уравнения Абеля, после ряда преобразований получим
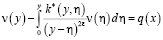 , (10)
, (10)
где 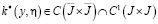 ,
, 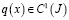 – известные функции.
– известные функции.
Уравнение (10) является интегральным уравнением Вольтера второго рода со слабой особенностью в ядре, которое однозначно и, безусловно, разрешимо в требуемом классе функций.
По найденному 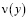 из (6) можно определить
из (6) можно определить 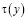 и решение задачи (1)-(4) в области D– по формуле (5), а в области D+ по формуле (7).
и решение задачи (1)-(4) в области D– по формуле (5), а в области D+ по формуле (7).



