Активной зоной называют глубину, где практически затухают напряжения от внешних нагрузок. На этой глубине величина сжатия грунтового слоя чрезвычайно мала. Для оценки прочности и устойчивости земляного полотна, определения межремонтных сроков и параметров мерзлотного режима необходим прогноз влажности грунтов. Поскольку влажность сама по себе является феноменологической характеристикой, количественная её оценка традиционно основана на феноменологической теории тепло- и массообмена с использованием методов классической термодинамики путем введения коэффициентов переноса влаги.
Однако плохая воспроизводимость результатов определения коэффициентов переноса влаги, наличие субъективизма, присущее всем упрощённым методикам, обусловило разработку более надёжных способов расчёта и прогнозирования влажности грунтов активной зоны земляного полотна инженерных сооружений. Одним из таких методов явился метод, основанный на решении нелинейного дифференциального уравнения изотермического переноса влаги, в результате чего коэффициент переноса влаги был заменён более надёжными, знакомыми и доступными параметрами.
Общие положения
Сопряженное уравнение диффузии влаги с законом сохранения энергии (уравнение неразрывности) записывается в виде [2]:
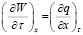. (1)
Поток влаги в грунт после инфильтрации осадков или в результате капиллярного поднятия определяется из соотношения:
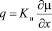, (2)
где Kн – коэффициент влагопроводности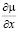 
– градиент потенциала влаги.
Из (1) и (2) определяем:
.
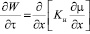Градиент потенциала, выраженный через градиент влажности:
;
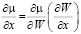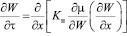– есть уравнение миграции влаги под действием градиента влажности и градиента потенциала. Действием силы тяжести прене6регаем, так как в ненасыщенных почво-грунтах супесчаных и суглинистых миграция влаги в изотермических условиях в большей степени зависит от потенциала влаги, чем от действия силы тяжести и площади инфильтрации.
Потенциал влаги и коэффициент влагопроводности определяется как функция влагосодержания:
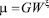и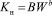 
.
Отсюда: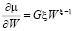 
и
.
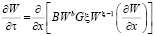Обозначим BGξ = A, b + ξ –1 = α.
Согласно [2] параметр ξ обычно равен –1 или –2, может иметь значение 1 или 2, тогда α может иметь значение 0, –1 или –2. Как показали опыты, наиболее вероятное значение α – это –1.
Тогда
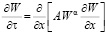, (3)
где А и α константы, зависящие от вида грунта.
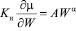есть Dk – обобщенный коэффициент диффузии (коэффициент диффузности). Уравнение (3) не совсем верно отражает реальные пpоцессы миграции влаги, когда возможно движение влаги против градиента влажности, но тем не менее с его помощью можно получить качественную картину влажностного режима и оценить ожидаемое значение величины влажности грунта земляного полотна.
Частное решение уравнения диффузивности
Если обобщённый коэффициент проводимости Dk представить в виде функции
Dk = Auα , (4)
то уравнение (4) приводится к виду
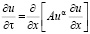, (5)
легко решаемое классическим методом разделения переменных.
Здесь А и α параметры, характеризующие проводящие свойства среды (грунта). После дифференцирования уравнения (5) и последующих преобразований при α = – 1 получено решение уравнения классическими методами математической физики [5]:
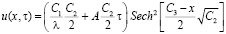, (6)
где х и τ – пространственно-временные координаты, а постоянные интегрирования С1, С2, С3, A и λ определяются из начальных и граничных условий.
Некоторые частные решения задачи изотермического увлажнения
Хотя полученное решение и не является вполне строгим, с его помощью оказалось возможным решить ряд практических задач. В частности, удалось получить более общее решение задачи увлажнения снизу от уровня грунтовых вод. При решении задачи увлажнения сверху это уравнение явилось основой эффективного использования метода гидролого-климатических расчетов В.С. Мезенцева [6]. Предварительные расчеты показали применимость его при решении и целого ряда других вопросов, например, температурного поля и вторичной консолидации слабых оснований, распределения по глубине напряжений, удельной поверхности почвогрунтов и содержания солей, моделирование движения транспортных потоков на автомобильных дорогах.
В настоящей работе даны решения изотермического увлажнения в зависимости от расчетной схемы: увлажнение только сверху, только снизу, двухстороннее увлажнение при глубоком и близком залегании грунтовых вод, для защищенного и незащищенного грунта. Влагонакопление происходит, главным образом, за счет диффузии влаги по порам [10].
Для закрытых грунтовых систем, у которых сверху, снизу или с боков имеются паро- и влагонепроницаемые слои, характерна эпюра распределения влаги, когда постоянная интегрирования С3 соответствует глубине максимальной конденсации водяных паров. В зависимости от климатических условий эта величина может быть от 20 до 60 см. Верхние слои незащищенного грунта увлажняются осадками, параметр С3 = 0.
При увлажнении снизу влажность на горизонте грунтовых вод изменяется в соответствии с колебаниями его положения относительно поверхности земли и равна полной влагоемкости (ωпв) при длительно стоящих грунтовых водах. В соответствии с положениями В.С. Мезенцева и А.А. Роде на уровне капиллярной каймы влажность грунта принимается равной наименьшей влагоемкости ωn [6, 8].
Расчёт влажности грунтов земляного полотна влагонакопления в условиях изотермического увлажнения в расчётный период
Из (6), заменяя u(x,τ) на ω(x,τ), получаем для расчёта влажности:
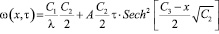. (7)
Формула (7) может быть модифицирована в зависимости от начальных и граничных условий, соответствующих той или иной схеме увлажнения земляного полотна.
С учетом этого в условиях одностороннего изотермического увлажнения сверху получено решение:
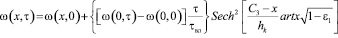, (8)
где
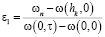. (9).
При ε ≤ 0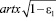 
= 5,3.
Начальное распределение влажности по глубине может быть постоянным или задано в виде функции ω(x,0). Объёмная влажность – ω(hk,0) на глубине равной hk от поверхности зависит от условий увлажнения. Влажность на поверхности может прогнозироваться регрессионными уравнениями [4], либо другими методами, например [9].
Если принять, что начальная влажность по глубине hk равна оптимальной, а влажность на поверхности может достигнуть полной влагоёмкости, тогда
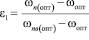
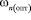– наименьшая влагоёмкость, соответствующая максимальному уплотнению при оптимальной влажности.
Длительность периода влагонакопления (τвл) принимается равной с начала осеннего влагонакопления и до конца весеннего периода, то есть:
τвл= τос + τпр + τвес. (3)
В период промерзания и в зимний период влагонакопление происходит за счет увлажнения снизу от уровня грунтовых вод.
,
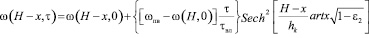где
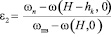. (10)
При этом были приняты следующие допущения: влажность грунта на уровне капиллярной каймы (hk) равна наименьшей влагоёмкости (ωn), а на глубине (Н) залегания подземных вод равна полной влагоёмкости (ωпв) [6, 8].
.
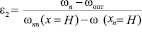В условиях двухстороннего увлажнения при меняющемся положении подземных вод для определения влажности грунта с учётом принципа суперпозиции получено решение:
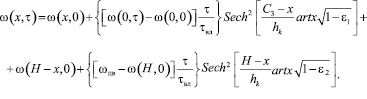(11)
При этом x принимает значения от нуля до z, а Н – x от z до Н. Величина z определяется подбором путём приравнивания обоих членов правой части уравнения (11) друг другу.
При длительно стоящих грунтовых водах
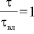и
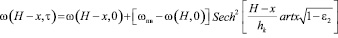. (12)
Средняя влажность грунтового массива в пределах от уровня подземных вод до верха капиллярной каймы, иначе капиллярная влагоёмкость, при начальной влажности равной ω0 определится из выражения:
.
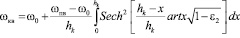После преобразований получаем:
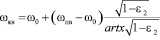. (13)
Учитывая, что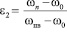 
, при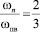 
[1, 6, 8] ωкв = 0,73ωпв.
Если ω0 = ωn и начальная влажность ω0 → 0, то ωкв = 0,87ωпв. (см. сравнительную таблица) получаем, что у В.С. Мезенцева ωкв = 0,80ωпв [6] дано только частное решение.
Сравнительные значения средней влажность грунтового массива в пределах от уровня подземных вод до верха капиллярной каймы (величины капиллярной влагоёмкости ωкв)
|
Начальное условие |
Капиллярная влагоёмкость |
|
ω0 = ωn |
ωкв = 0,73ωпв |
|
ω0 → 0 |
ωкв = 0,87ωпв |
|
у В.С. Мезенцева |
ωкв = 0,80ωпв |
Таким образом, мы получили более общее решение для определения средней влажность грунтового массива в пределах от уровня подземных вод до верха капиллярной каймы (величины капиллярной влагоёмкости ωкв).
Средняя влажность грунта в пределах активной зоны ha (зона аэрации) определяется интегрированием уравнения (11):
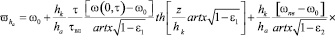
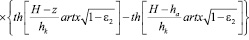. (14)
Величина z определяется из выражения:
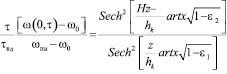. (15)
Влажность грунта на поверхности ω(0,τ) может прогнозироваться регрессионными уравнениями [4] или любыми другими методами, например по методу профессора В.С. Мезенцева [6] или Рувинского В.И. [9]. В первом приближении ω(0, τ) может быть принята равной (0,7 – 0,9) ωпв. Длительность периода влагонакопления принимается равной с начала осеннего влагонакопления и до конца весеннего периода.
Расчёт и прогнозирование влажности грунтов земляного полотна во внутригодовом цикле
Во многих случаях при решении задач прочности и надёжности дорожных конструкций возникает необходимость прогнозирования влажности грунтов во внутригодовом цикле. При решении задачи увлажнения сверху применён принцип суперпозиции с использованием метода гидролого-климатических расчётов В.С. Мезенцева [6]. Из (14):
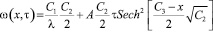
Обозначим ω(x,τ) как ω(x, i) и ω(x, i-1) то есть как влажность в момент времени i и i – 1. Тогда при х = 0
.
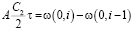По В.С. Мезенцеву [6], влажность грунта, выраженная в объёмных единицах (г/см3) на поверхности в момент времени i, равна:
.
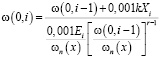Тогда
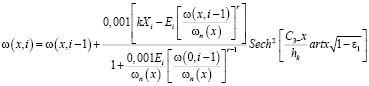. (16)
Здесь kXi, Ei – сумма осадков и испаряемость, выраженная в (мм) за время от i –1 до i; ωn(x) – наименьшая влагоёмкость на глубине x, выраженная в объёмных единицах (г/см3); r – параметр, характеризующий гидрофизические свойства грунтов [6]. Численное значение этого параметра можно принять равным высоте капиллярного поднятия, выраженное в метрах.
Влажность грунта на глубине х для тёплого периода года в условиях Западной Сибири и Северного Казахстана рассчитывается по формуле (16) помесячно, начиная с апреля (i = 4) по октябрь (i = 10) включительно.
В период промерзания и в зимний период с ноября по март включительно влагонакопление происходит за счет увлажнения снизу от уровня грунтовых вод:
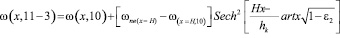(17)
Параметры С3, ε1, ε2 определяются из начальных и граничных условий в зависимости от расчётной схемы увлажнения.
Если принять, что в начальный момент времени грунт земляного полотна был уплотнён при оптимальной влажности до соответствующей плотности и в процессе увлажнения сверху влажность на поверхности достигнет полной влагоёмкости, а на уровне капиллярной каймы наименьшей влагоёмкости, тогда:
.
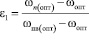То же при увлажнении снизу от уровня подземных вод:
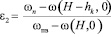
Здесь индекс ω означает объёмную влажность; ωопт – оптимальная влажность, ωn(опт) – наименьшая влагоёмкость, соответствующая оптимальному уплотнению; ωпв(опт) – полная влагоёмкость, соответствующая оптимальному уплотнению; ωпв(Н) – полная влагоёмкость грунта на глубине Н, соответствующая уровню подземных вод; ωn(Н) – наименьшая влагоёмкость, соответствующая уровню подземных вод. Учитывая, что наименьшая влагоёмкость составляет 0,6 – 0,8 от полной влагоёмкости [6, 8], были установлены следующие соотношения:
,
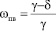где γ – плотность частиц грунта; δ – плотность скелета грунта.
Параметр С3 зависит от степени паро- и влагонепроницаемости покрытий. Для паро- и влагонепроницаемости покрытий, изготовленных с применением органических вяжущих С3 = 40 – 60 см. Для остальных покрытий С3 = 0 – 20 см.
При послойном расчёте влажности грунтов используются формулы (16), (17). Исходной информацией является: климатические характеристики местности, параметры гидрофизических свойств грунтов и параметры элементов дорожных конструкций. Испаряемость для условий Западной Сибири и Северного Казахстана, как показали наши исследования, можно рассчитать по уравнениям В.С. Мезенцева [6]. Высоту капиллярного поднятия hк и параметр r для лёгких грунтов (песок, супесь) можно принять равным 1 – 1,4, средних грунтов (суглинки лёгкие и средние) 1,4 – 2,0 и тяжёлых (суглинки тяжёлые, глины) 2 – 3 [6].
Начальное распределение влажности по глубине может быть принято равномерным или в виде функции от х. Соответственно этому рассчитывается наименьшая влагоёмкость, используя вышеприведённые зависимости. Расчёт начинают с определения зимней влажности по формуле (17). Затем по формуле (16) определяют влажность помесячно, начиная с 4-го, принимая ω(x,i–1) равным ω(x,i) при i = 11 – 3. Снова определяют зимнюю влажность, подставляя в формулу (17) ω(x,i-1), рассчитанную по уравнению формуле (16). Расчёты повторяют до тех пор пока следующее значение влажности не будет отличаться от предыдущего на заранее определённую величину, например на 0,1 %. В зависимости от положения подземных вод число циклов расчёта может составлять от 6 до нескольких десятков. Поэтому при послойном расчёте влажности целесообразно использовать ЭВМ.
Алгоритмы, описанные вышеприведёнными уравнениями, реализованы на ЭВМ для различных типов грунтов при различном уровне подземных вод для различных пунктов Западной Сибири и Северного Казахстана с 1965 г. Аналогичным образом получены уравнения для прогнозирования средней влажности грунта в пределах активной зоны ha (зоны аэрации) во внутригодовом цикле:
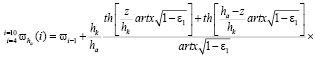
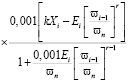. (18)
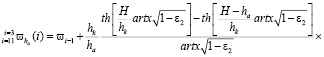
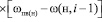. (19)
Здесь i – 1 принимается 10-й месяц года.
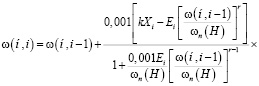
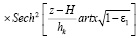. (20)
В первом приближении параметр z можно принимать равным С3 то есть 40 – 60 см. При расчёте влажности во внутригодовом цикле вначале по формуле (20) определяют влажность на глубине Н (то есть на уровне подземных вод) в 10-м месяце (в начале периода промерзания), задаваясь ω(Н,i–1)=ωпв(Н). Осадки и испаряемость при этом определяют для октября месяца (i = 10). Затем по формуле (19) определяют влажность в конце зимнего периода влагонакопления, принимая среднюю влажность в зоне ha в 10-м месяце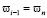 
. После последовательно с апреля по октябрь определяют среднюю влажность по формуле (18) до тех пор пока не будет достигнута необходимая степень сходимости.
Проведённые расчёты показали, что независимо от начальных условий (начальную влажность можно даже принимать равной нулю) через определённое количество циклов будет достигнуто квазистационарное состояние. Это позволяет рекомендовать предложенный метод для прогнозирования влажности в многолетнем цикле. Основными преимуществами этого метода являются:
– отпадает необходимость определять столь непредсказуемый и капризный коэффициент влагопроводности (диффузивности) грунтов;
– возможность применения в любой дорожно-климатической зоне, для любого типа увлажнения местности;
– простота и удобство расчётов.
Основные выводы
1. Разработан метод прогнозирования влажности грунтов на основе решения нелинейного дифференциального уравнения теплопроводности. Так как в одном из частных решений использована методика В.С. Мезенцева, разработанная для грунтов открытого поля, то результаты расчётoв требуют уточнения с целью учёта испарения и впитывания влаги.
2. Проведено районирование территории Западной Сибири по параметрам влажностного режима.